Спектр линейного оператора

Множество всех собственных значений линейного оператора называется его спектром.

Спектр линейного оператора зависит от того каковы корни характеристического многочлена.

17°. В комплексном векторном пространстве V каждый линейный оператор А имеет, по крайней мере, хотя бы один собственный вектор и следовательно в V существует, по крайней мере, одно одномерное инвариантное относительно А подпространство.

◀ Справедливость этого следует из «основной теоремы алгебры». ▶

Более того j(l) = 0 в комплексном пространстве V имеет ровно n корней, с учетом их кратности: λ₁, λ₂, …, λ _n.

=

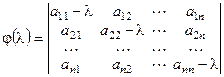с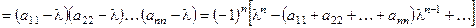. С другой стороны

18°. λ₁ + λ₂ + … + λ _n = a ₁₁ + a ₁₁ + … + a_nn = tr A = Sp A.

(trace) (Spur)

англ. нем.

◀ Величина a ₁₁ + a ₁₁ + … + a_nn называется следом матрицы А, но т.к. характеристический полином не зависит от выбора базиса то и Sp A не зависит от базиса и называется следом линейного оператора. ▶

19°. Для всякого линейного оператора А в вещественном пространстве размерности n >2 существует одномерное или двухмерное инвариантное подпространство.

◀ Если j(l) = 0 имеет хотя бы один вещественный корень λ₀ то оператор А имеет собственный вектор и, следовательно, одномерное инвариантное относительно А подпространство.

Если j(l) = 0 не имеет вещественных корней, то существует комплексный корень l = a + b i. Решая относительно этого λ систему Az = l z, найдем комплексное решение z = x + iy. Т.е.

A (x + iy) = (a + i b)(x + iy) = (a x – b у) + i (b x + a y).

Приравнивая, вещественные и мнимые части правой и левой части равенства получим:. Отсюда ясно, что ℒ(x, y) есть подпространство, инвариантное относительно оператора А. ▶

И, наконец, еще два утверждения о спектре линейного оператора.

20°. Если λ₁, λ₂, …, λ _n – все собственные значения оператора А, с учетом их кратностей и f (t) произвольный многочлен, то f (λ₁), f (λ₂), …, f (λ _n ) – это все собственные значения оператора f (А), причем кратность f (λ _i) такая же как и кратность λ _і (собственные векторы при это не меняются).

Доказать самостоятельно.

21°. Если Ах = λ₀ х и detA ¹ 0, то существует А ^–1 и кроме того .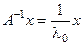

◀ Ах = λ₀ х. Действуем оператором А ^–1. А ^–1 Аx = λ₀ А ^–1 Þ 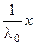= А ^–1 x. ▶

РАЗДЕЛ 8. Преобразования при изменении базиса

Дата добавления: 2014-01-11