Скалярное поле

Некоторые приложения криволинейного интеграла II рода

1. Площадь плоской фигуры.

Площадь S плоской фигуры, расположенной в плоскости Оху и ограниченной замкнутой линией L, можно найти по формуле

Пример.

Найти площадь фигуры, ограниченной астроидой 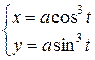(рис. 25).

Кривая задана параметрическими уравнениями.

Рис. 25

Находим , , параметр t изменяется от 0 до 2π.

Составляем интеграл:

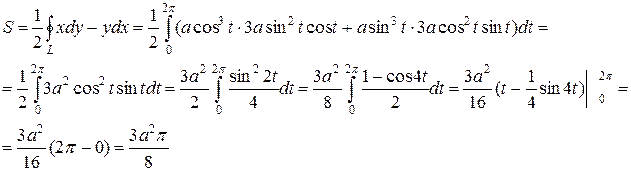
2. Работа переменной силы

Переменная сила на криволинейном участке АВ производит работу, которая находится по формуле .

Пример: Найти работу силы 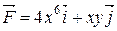вдоль кривой от очки О(0;0) до точки В(1;1).

Вопросы для самоконтроля.

1. Задача, приводящая к понятию криволинейного интеграла.

2. Свойства криволинейных интегралов.

3. Вычисление криволинейных интегралов.

4. Между какими интегралами устанавливает связь формула Остроградского-Грина?

5. Условия независимости криволинейного интеграла II рода от пути интегрирования.

6. Приложения криволинейных интегралов.

Литература: [5] стр. 217-228, [6] стр. 407-418, [7] стр. 470-474.

Примеры: [2] стр. 47-52, [3] стр. 103-114, 119-127.

3. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

Теория поля – крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.

К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы – все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т.д.

Рассмотрим скалярные и векторные поля.

Скалярным полем называется область пространства, если каждой точке М этой области соответствует определенное число U(М).

Другими словами: если в пространстве (х, y, z) имеется область D, в которой задана функция U=U(x,y,z), то говорят, что в области D задано скалярное поле.

Пример:

1) если U(x,y,z) – обозначает температуру в точке М, то говорят, что задано скалярное поле температур: в некоторой декартовой системе координат находится неравномерно нагретое тело и температура его в каждой точке М(x,y,z) известна t˚=U(M). Тогда часть пространства, занятая телом, будет скалярным полем температур данного тела;

2) скалярное поле атмосферного давления, плотности (массы, воздуха), поле влажности;

3) скалярное поле солености воды (устье реки впадающей в море).

Если скалярная величина U(M) не зависит от времени то поле называется стационарным (или установившимся).

Поле, которое меняется с течением времени, называется нестационарным.

Пример: поле температуры при охлаждении тела, поле влажности – нестационарное поле, поле плотности данного тела – стационарное.

Если функция зависит только от двух координат x и y, то поле функции U(M)=U(x,y) называется плоскопараллельным.

Дата добавления: 2014-01-11