Представление непериодической функции рядом Фурье

Пусть f(x) - непериодическая функция, заданная на всей числовой оси. Так как сумма тригонометрического ряда является периодической функцией, то, очевидно, что данная непериодическая функция не может быть разложена в ряд Фурье.

Однако непериодическая функция f(x) может быть представлена в виде ряда Фурье на любом конечном промежутке 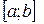, на котором она удовлетворяет условиям Дирихле. Для этого можно поместить начало координат в середину отрезка 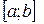и построить функцию f₁(x) периода 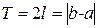такую, что f₁(x)=f(x) при .

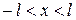Разлагаем функцию f₁(x) в ряд Фурье. Сумма этого ряда во всех точках отрезка 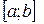(кроме точек разрыва) совпадает с заданной функцией f(x). Вне этого промежутка сумма ряда и f(x) являются совершенно различными функциями.

Иногда приходится иметь дело с функциями, заданными только в интервале 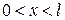. В этом случае мы можем сначала продолжить (доопределить) по какому-либо закону функцию на интервал 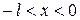, а затем продолжить ее на всю числовую прямую периодически с периодом 2l. Продолжить функцию из интервала 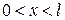на интервал 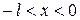можно произвольным образом.

Чаще всего продолжают четным или нечетным образом. Если функция продолжается четным образом (т.е. чтобы при 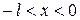было f(x)= f(-x)), то ряд Фурье содержит только косинусы и свободный член. Если же функция продолжается нечетным образом, то ряд Фурье содержит только синусы.

Ряд косинусов и ряд синусов для функции f(x), заданной на отрезке 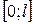, имеют одну и ту же сумму. Если х₀ - точка разрыва функции f(x), то сумма как одного, так и другого ряда равна одному и тому же числу: .

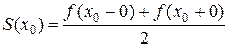Замечание. Все выше сказанное справедливо для функции f(x), заданной на отрезке 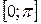. Такую функцию можно разложить как в ряд косинусов, так и вряд синусов.

Пример. Разложить в ряд косинусов функцию , .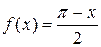

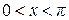Решение. Продолжим функцию f(x) на отрезок 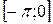четным образом.

Разлагаем в ряд функцию 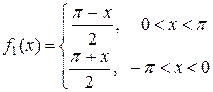с периодом Т=2π.

Функция f₁(x) удовлетворяет условиям теоремы Дирихле, поэтому

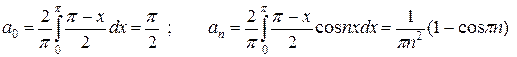
Таким образом ,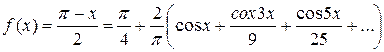

где .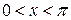

Вопросы для самоконтроля.

1. Какие процессы называются периодическими? Привести пример периодических процессов.

2. Простейший периодический процесс. Функция простейшего периодического процесса.

3. Тригонометрический ряд Фурье.

4. Теорема Дирихле.

5. Разложение в ряд Фурье четных и нечетных функций.

6. Разложение в ряд Фурье функций произвольного периода.

7. Разложение непериодической функции в ряд Фурье на отрезке .

Литература: [5] стр. 328-343, [6] стр. 478-489, [7] стр. 400-410.

Примеры: [2] стр. 106-112, [3] стр. 190-235.

Дата добавления: 2014-01-11