Линеаризация нелинейных ММ

Линеаризация является наиболее распространенным способом понижения уровня сложности ММ и служит основой применения линейной теории.

Суть любой линеаризации состоит в приближенной замене исходной нелинейной зависимости (нелинейности) некоторой линейной зависимостью в соответствии с определенным условием (критерием) эквивалентности. Среди возможных методов чаще всего применяют метод касательных (линеаризация в малой окрестности заданной точки). Этот метод не зависит от вида преобразуемых сигналов и может одинаково успешно использоваться для разных типов нелинейностей, которые могут быть одномерными и многомерными; безынерционными (статическими) и динамическими.

Безынерционные нелинейности устанавливают функциональную зависимость между значениями входа u (t) и выхода y (t) в один и тот же текущий момент времени t и могут задаваться либо явно (формулами, графиками, таблицами), либо неявно (алгебраическими уравнениями). На структурных схемах им соответствуют безынерционные (без памяти) нелинейные звенья.

Динамические нелинейности описываются математически нелинейными дифференциальными уравнениями и на структурных схемах им соответствуют нелинейные динамические звенья. При этом значения выхода y (t) в текущий момент времени t зависят не только от значений входа в этот же момент времени, но и от производных, интегралов или каких либо других значений.

Математической основой метода касательных является разложение нелинейной функции в ряд Тейлора в малой окрестности некоторой «точки линеаризации» с последующим отбрасыванием нелинейных слагаемых, содержащих степени отклонений переменных (приращений) выше первой.

Суть метода рассмотрим на частных случаях с последующими обобщениями.

1) Пусть y = F (u) - явно заданная одномерная безынерционная нелинейность, гладкая и непрерывная в окрестности некоторой точки u = u *. Полагая, u = u *+D u; y = y *+D y, где y *= F (u *), запишем ряд Тейлора для этой функции в виде:

(1)

Отбрасывая слагаемые более высокого порядка малости, и оставляя только слагаемые, содержащие D u в первой степени, получим приближенное равенство

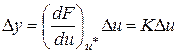. (2)

Это выражение приближенно описывает взаимосвязь малых приращений D y и D u в виде линейной зависимости и является результатом линеаризации в рассматриваемом случае. Здесь К имеет геометрический смысл углового коэффициента наклона касательной к графику функции в точке с координатой u = u *.

В случае многомерной нелинейности y = F (u), когда y ={ y_i }, F ={ F_i } и u ={ u_j }– векторы, аналогично получим, что D y = K D u. Здесь K ={ K_ij }- матричный коэффициент, элементы которого K_ij определяются как значения частных производных функций F_i по переменным u_j, вычисленных в «точке» u = u*.

2. Пусть безынерционная нелинейность задана неявно с помощью алгебраического уравнения F (y, u)= 0. Необходимо линеаризовать эту нелинейность в малой окрестности некоторого известного частного решения (u *, y *) в предположении того, что все нелинейные функции F_i в составе F непрерывны и дифференцируемы в этой окрестности. Выполнив разложение этой вектор-функции в ряд Тейлора и, отбросив слагаемые второго и выше порядков малости, получим линейное уравнение первого приближения:

, (3)

где D y = y – y *; D u = u – u *; - матрицы частных производных, вычисленные в точке линеаризации.

3. Пусть одномерная динамическая нелинейность задана дифференциальным уравнением «вход-выход» n -го порядка:

F (y, y ⁽¹⁾, …, y ^{( n )}, u, u ⁽¹⁾, … u ^{( m )})=0. (4)

Линеаризуем эту нелинейность методом касательных в малой окрестности известного частного решения этого уравнения y *(t), соответствующего заданному входу u *(t). Производные по времени соответствующих порядков от y *(t) и u *(t) также предполагаются известными.

Предполагая функцию F непрерывно-дифференцируемой по всем своим аргументам и следуя рассмотренной выше общей методике (разложение в ряд и учет только линейных относительно приращений аргументов слагаемых), запишем линейное уравнение первого приближения для нелинейного уравнения:

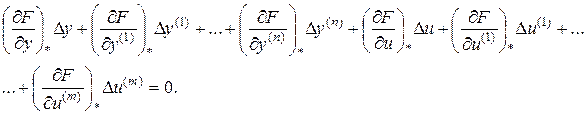(5)

Здесь символ (*) означает, что частные производные определены при значениях переменных и их производных, соответствующих частному решению (y *(t), u *(t)). В общем случае их значения (коэффициенты уравнения) будут зависеть от времени и линеаризованная модель будет нестационарной. Но если частное решение соответствует статическому режиму, то эти коэффициенты будут постоянными.

Для удобства и краткости записи, введем следующие обозначения:

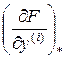= a_i; = - b_i; D y ⁽ⁱ⁾= Dⁱ D y; D u ⁽ⁱ⁾= Dⁱ D u; D = d / dt.

Тогда линеаризованное уравнение (5) запишется в краткой операторной форме:

A (D)D y (t)= B (D)D u (t),

где A (D) – полином степени n относительно оператора дифференцирования D;

B (D) – аналогичный операторный полином m -ой степени.

4. Пусть многомерная динамическая нелинейность задана нелинейными уравнениями состояния вида

(6)

Аналогично предыдущим случаям, линеаризуем эту нелинейность методом касательных в малой окрестности известного частного решения (x*, y*), соответствующего заданному входу u* (t). При этом уравнения первого приближения будут иметь следующий вид:

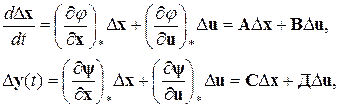(7)

где - матрицы соответствующих размеров. Их элементы в общем случае будут функциями времени, но если частное решение соответствует статическому режиму, то они будут постоянны.

Сделаем заключительные замечания о применении метода касательных при линеаризации ММ всей САР, представляющей собой совокупность описаний взаимодействующих между собой конструктивных блоков.

1) «опорный режим» (*), относительно которого выполняется линеаризация, рассчитывается для всей системы по ее полной (нелинейной) ММ. Для расчета могут использоваться как графические, так и численные (компьютерные) методы. При этом коэффициенты всех линеаризованных уравнений и функциональных зависимостей будут зависеть от выбранных точек линеаризации;

2) все нелинейные зависимости ММ должны быть непрерывными и непрерывно дифференцируемыми (гладкими) в малой окрестности режима (*);

3) отклонения переменных от их значений в опорном режиме должны быть достаточно малыми; для САР и У это требование вполне согласуется с целью управления – регулированием значений управляемых переменных в соответствии с предписанными законами их изменения;

4) для линейных уравнений в составе ММ линеаризация состоит в формальной замене всех переменных на их отклонения (приращения);

5) для получения линеаризованной ММ всей системы в стандартном виде, например в форме уравнений состояния, следует сначала проводить линеаризацию каждого из уравнений в составе ММ. Это будет намного проще и быстрее, чем попытка получения нелинейной ММ системы в стандартном виде с последующей ее линеаризацией;

6) при соблюдении всех условий применения метода касательных, свойства линеаризованной ММ дают объективное представление о локальных свойствах нелинейной ММ в малой окрестности опорного режима. Этот факт имеет строгое математическое обоснование в виде теорем Ляпунова (первый метод) и является теоретической базой для практического применения линейной теории управления.

Дата добавления: 2014-01-11