Методы временной области

ОСНОВЫ ЛИНЕЙНОЙ ТЕОРИИ УПРАВЛЕНИЯ

Линейная теория управления – это раздел общей теории управления, в котором для исследования (анализа) САУ и для решения задач синтеза используются линейные ММ, не содержащие нелинейных зависимостей между переменными. Такие ММ получены в результате применения процедур идеализации и линеаризации. При этом вместо реальных звеньев рассматриваются их линейные модели в виде абстрактных однонаправленных линейных динамических звеньев (ЛДЗ), а вместо реальных САУ – линейные динамические системы (ЛДС). Структурные схемы ЛДС представляют собой соединения ЛДЗ. Если ЛДС входит в состав другой системы, то она сама является сложным динамическим звеном. В то же время, при необходимости, сложные ЛДЗ можно представить соединением более простых или даже элементарных (неделимых) звеньев, рассматривая их как ЛДС. В общем случае как ЛДЗ, так и ЛДС могут быть многомерными и иметь несколько входов и/или выходов.

Для описания свойств ЛДЗ и ЛДС, а также для их исследования могут применяться методы временной, комплексной и частотной областей.

Входные и выходные сигналы ЛДЗ (или ЛДС) рассматриваются как некоторые функции времени, а ЛДЗ преобразует входные сигналы u (t)=(u ₁, u ₂, …, u_m) в выходные сигналы y (t)=(y ₁, y ₂, …, y_n) в соответствии с некоторым математическим правилом – оператором преобразования А _t: y (t)= A _t { u (t)}(рис.1). Индекс (.) _t в обозначении оператора показывает, что в А _t входят математические операции, имеющие смысл для функций непрерывно изменяющегося аргумента t. Такие звенья и их операторы называются непрерывными. Они преобразуют входной непрерывный сигнал в выходной, тоже непрерывный, сигнал. В том случае, когда оператор звена А _k определен на множестве функций, аргумент которых может принимать только разрешенные (дискретные) значения t_k = kT ₀ при k =0, 1, 2, …, то он и соответствующее ему звено называются дискретными.

Рис.1

Если ЛДЗ многомерное, то его оператор преобразования представляет собой матрицу (таблицу) А _t ={ 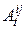}, где 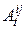– одномерный оператор, устанавливающий связь j -го входа и i -го выхода. Тип оператора преобразования определяет тип ЛДЗ. Различают следующие их разновидности.

1. Если ЛДЗ и его оператор А _t преобразуют ограниченны й входной сигнал в выходной сигнал, также ограниченный по величине (без разрывов второго рода), то их называют физически осуществимыми.

2. Если выходы в текущий момент времени t определяются б ез использования будущих значений входных сигналов, то ЛДЗ и А _t физически реализуемы.

3. Если сдвиг по времени входного сигнала приводит к такому же сдвигу выходного сигнала без изменения его формы, то ЛДЗ и его оператор называются стационарными: A_t { u (t –τ)} = y (t –τ).

4. Для детерминированного звена (и оператора) можно определить точное значение выхода в любой момент времени, если известны ММ и закон изменения входа звена. Для стохастического (недетерминированного) оператора выход можно определить лишь в вероятностном смысле, т.е. найти его статистические характеристики.

5. Сложный (составной) оператор преобразования представляется некоторой композицией более простых операторов. Ему соответствует структурное представление (схема) в виде соединения однонаправленных звеньев с более простыми операторами преобразования.

6. Для линейного оператора преобразования A_t всегда выполняется условие:

.

Оператор преобразования ЛДЗ может быть задан явно (формулой), либо неявно (с помощью одного или нескольких уравнений). Кроме того, для быстрого получения информации о свойствах ЛДЗ используются его временные характеристики (весовая и переходная функции). При этом, как правило, для неявного задания оператора ЛДЗ применяют канонические формы для ММ в виде а) уравнение «вход-выход» и б) уравнения состояния. Рассмотрим эти случаи подробно.

Дата добавления: 2014-01-11