Временные характеристики ЛДЗ и его оператора преобразования

Важной особенностью ЛДЗ является то, что их свойства полностью проявляются (а значит и могут быть изучены!) в их реакциях на простейшие виды типовых входных воздействий таких как а) импульсная d-функция и б) единичная ступенчатая функция:

а) u (t)=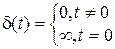при условии ;

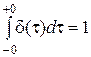б) u (t)=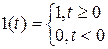; при этом и (формально!) .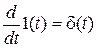

Поскольку реакция звена на любое воздействие зависит от состояния звена в момент подачи воздействия на него, то (для определенности) при изучении свойств ЛДЗ по их временным характеристикам полагают, что до подачи воздействий ЛДЗ находилось в состоянии покоя. Это соответствует нулевым начальным условиям для выхода звена и для его производных.

Весовая функция ЛДЗ w (t). Это реакция находящегося в покое линейного звена на импульсное воздействие в виде d-функции: w (t)= A_t {d(t)}.

· Для физически реализуемого звена w (t)=0 при t <0. Это соответствует «физическому смыслу» весовой функции, т.к. реакция не может опережать во времени причину ее появления.

· По виду графика w (t) можно судить о характере процесса в ЛДЗ (колебательный, апериодический, затухающий, расходящийся); о времени и интенсивности его затухания; о максимальном отклонении процесса.

· Если w (t)®0 при t ®∞, то ЛДЗ будет устойчивым (асимптотически), т.к. оно возвращается в первоначальное (нулевое) состояние после прекращения действия возмущения. Если условие затухания не выполняется, то ЛДЗ либо неустойчиво, либо находится на границе устойчивости.

· Весовая функция позволяет получить реакцию находящегося в покое ЛДЗ на произвольное внешнее воздействие u (t). Это следует из следующих соотношений.

Пусть y (t)= A_t { u (t)}, где u (t)=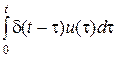. Тогда y (t)= A_t {}=

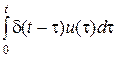=(формула свертки).

Таким образом, весовая функция характеризует все основные собственные динамические и преобразовательные свойства ЛДЗ и с ее помощью оператор A_t задается явно в виде формулы свертки.

Переходная функция ЛДЗ h (t). Это реакция находящегося в покое линейного звена на воздействие в виде единичной ступенчатой функции: h (t)= A_t {1(t)}.

· Переходная функция ЛДЗ связана с его весовой функцией следующим образом: h (t)= A_t {1(t)} = A_t {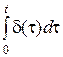}= 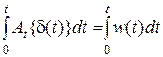. Отсюда следует .

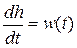В отличие от w (t), h (t) можно определить экспериментально.

· Для физически реализуемого звена h (t)=0 при t <0. Это соответствует ее физическому смыслу и принципу причинности.

· По виду графика h (t) можно судить о характере процесса в ЛДЗ; о времени и интенсивности его затухания; о максимальном отклонении (выбросе) процесса от установившегося значения и т.п.

· Если h (t)®const при t ®∞, то ЛДЗ будет асимптотически устойчивым, т.к. при этом соответствующая весовая функция w (t) будет асимптотически стремиться к нулю. Если это условие устойчивости не выполняется, то ЛДЗ либо неустойчиво, либо находится на апериодической или на колебательной границе устойчивости.

· С переходной функцией связывают условие физической осуществимости, как требование отсутствия в h (t) разрывов второго рода (бесконечных «скачков». В этом случае ЛДЗ и его оператор A_t могут служить моделями некоторого реального звена, которое преобразует ограниченный по величине сигнал входа в выходной, тоже ограниченный сигнал.

2.1.2 Задание оператора преобразования уравнением «вход-выход»

Рассмотрим одномерное, непрерывное, стационарное ЛДЗ с оператором преобразования A_t, который задан неявно линейным дифференциальным уравнением

A (D) y (t)= B (D) u (t),

где A (D) = a ₀+ a ₁ D + a ₂ D ²+…+ a_nDⁿ, B (D) = b ₀+ b ₁ D + b ₂ D ² +…+ b_mD^m, D = d / dt.

Общее решение этого уравнения имеет две составляющих: y (t)= y ₁(t)+ y ₂(t), где y ₂(t) – некоторое частное решение, а y ₁(t) – свободная составляющая решения.

Если частное решение y ₂(t) записывается в форме вынуждающей функции u (t), то в теории управления его называют вынужденной (установившейся) составляющей y ₂(t)= y _в(t) выходного сигнала. При этом y ₁(t)= y _п(t) называют переходной составляющей процесса на выходе ЛДЗ.

Если y_п(t)®0 при t ®∞, то ЛДЗ называется устойчивым (асимптотически). В противном случае ЛДЗ либо неустойчиво (y _п(t) не затухает, а возрастает по величине), либо находится на границе устойчивости. При этом может быть два вида границы устойчивости: а) колебательная, когда y _п(t) имеет вид гармонических колебаний и б) апериодическая, когда y _п(t)=const.

Для выяснения математических условий устойчивости, рассмотрим выражение для переходной составляющей процесса

,

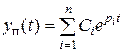где p_i – корни характеристического полинома A (p) = A (D) при D=p. В таком виде формула для y _п(t) справедлива, когда все характеристические корни различны. В случае кратного корня p_i, соответствующий ему коэффициент C_i в формуле будет полиномиальной функцией времени (степень полинома меньше коэффициента кратности корня на единицу).

В общем случае эти корни будут к о мплексными (p_i= α _i + j b _i), а общее их число (с учетом кратности) равно n. При этом парциальная составляющая для корня p_i имеет вид 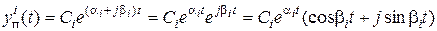. Она будет затухать во времени только при α _i = Re p_i < 0 («левый» корень). Если хотя бы для одного корня α _i >0 («правый» корень), то соответствующая ему парциальная составляющая процесса со временем увеличивает свои значения и ЛДЗ будет неустойчивым. При отсутствии правых корней, но при наличии пары сопряженных корней на мнимой оси (p_i,i+1= ± j b _i), ЛДЗ будет находиться на колебательной границе устойчивости. Если один корень нулевой (p_i = 0), а остальные – «левые», то ЛДЗ находится на апериодической границе устойчивости.

Таким образом, для устойчивости ЛДЗ необходимо и достаточно, чтобы все корни характеристического уравнения A (p)=0 были «левыми», т.е. имели отрицательные вещественные части и принадлежали левой полуплоскости.

Устойчивость является важным свойством динамических систем и понимается, как их способность возвращаться в первоначальное (невозмущенное) состояние после прекращения действия возмущений. Таким невозмущенным состоянием может быть, например, некоторый установившийся (вынужденный) режим, описываемый каким-либо частным решением уравнений динамики системы. В частности, это может быть статический (опорный) режим, относительно которого производилась линеаризация.

Характеристические корни { p_i } определяют свойство устойчивости (или неустойчивости), но зависят они сложным образом от значений коэффициентов полинома A (p). Аналитический вид этих зависимостей можно найти только в простейших случаях для полиномов не выше второго порядка. В более сложных случаях численные значения корней можно определить численными методами. Но для исследования устойчивости нужно знать не значения корней, а их положение относительно мнимой оси комплексной плоскости. В математике известны правила и условия, позволяющие судить о «левом» расположении корней полиномов непосредственно по их коэффициентам. Их называют алгебраическими критериями устойчивости.

Наиболее известными из них являются: а) необходимый критерий устойчивости Стодолы; б) критерий Рауса; в) критерий Гурвица и критерий Льенара-Шипара.

а) критерий Стодолы устанавливает необходимое условие устойчивости в виде требования положительности (или отрицательности) всех коэффициентов полинома A (p). При невыполнении условий этого критерия, ЛДЗ либо неустойчиво, либо находится на границе устойчивости.

б) критерий Рауса имеет табличную форму: по специальному алгоритму заполняются клетки таблицы Рауса и проверяются знаки элементов ее первого столбца. Положительность всех этих элементов гарантирует «левое» расположение всех корней полинома и, следовательно, и устойчивость ЛДЗ.

в) критерий Гурвица имеет аналитическую форму и более удобен в применении. Здесь предварительно составляется матрица Гурвица размером nxn по следующему правилу: вектор коэффициентов (a_n–1, a_n–2, …, a ₁, a ₀) располагается по главной диагонали, а затем заполняется нижний треугольник матрицы по столбцам (вниз от диагонального элемента) в порядке возрастания индексов коэффициентов. Верхний треугольник заполняется так же, но вверх от диагонали и в порядке убывания индексов. Элементы с несуществующими индексами равны нулю.

Затем для полученной матрицы записываются и вычисляются все главные диагональные миноры D₁, D₂, D₃, …, D _{n -1}, D _n. Если все эти миноры (определители Гурвица) положительны, то ЛДЗ устойчиво. В противном случае оно либо неустойчиво, либо на границе устойчивости. Колебательной границе соответствует, при всех a_i >0 и положительных минорах D₁, D₂, D₃, …, D _{n -2}, условие D _{n -1}=0.

Апериодической границе устойчивости соответствует, при положительных минорах D₁, D₂, D₃, …, D _{n -1}, условие a ₀=0.

Эти граничные условия удобно использовать при определении областей устойчивости замкнутых САР в плоскости каких-либо двух параметров системы g₁ и g₂.

Критерий Льенара-Шипара, по сути, является модификацией критерия Гурвица: при a_i >0 (i =0, 1, …, n) для устойчивости ЛДЗ c четным n требуется положительность определителей Гурвица нечетных порядков, а для нечетного n, положительность определителей четных порядков.

Исследование ЛДЗ на устойчивость, например по критерию при n =1 и n =2 показывают, что условие положительности коэффициентов (необходимое условие), в этих простых случаях является и достаточным для «левого» расположения корней. Если n >2, то для устойчивости обязательно выполнение дополнительных условий в виде неравенств на соотношение коэффициентов.

Так, например, при n =3 A (p)= a ₀+ a ₁ p + a ₂ p ²+ a ₃ p ³ кроме a_i> 0 еще необходимо и достаточно, чтобы выполнялось неравенство a ₁ a ₂- a ₀ a ₃>0. Случай равенства в этом выражении соответствует колебательной границе.

При n =4 A (p)= a ₀+ a ₁ p + a ₂ p ²+ a ₃ p ³+ a ₄ p ⁴ и для «левого» расположения корней необходимо и достаточно, чтобы a ₁(a ₂ a ₃- a ₁ a ₄) - a ₀ a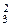 >0. Случай равенства нулю в этом выражении соответствует колебательной границе устойчивости.

Дата добавления: 2014-01-11