Алгебраические коэффициентные методы

Исходными данными для методов этой группы являются коэффициенты характеристического полинома. При этом используются следующие алгебраические критерии устойчивости:

а) необходимый критерий устойчивости (критерий Стодолы);

б) критерий Рауса;

в) критерий Гурвица;

г) критерий Льенара – Шипара.

а) необходимое условие устойчивости (критерий Стодолы). Рассмотрим ЛДС n -го порядка с характеристическим полиномом

A (p)= a ₀ + a ₁ p +... + a_npⁿ. (1)

Пусть, для определенности, a_n >0 (в противном случае все коэффициенты можно умножить на (–1), что не изменит корней полинома). Запишем этот полином в факторизованной форме, выделяя отдельно множители, соответствующие вещественным корням (p_i =a _i) и комплексно-сопряженным корням (p_k =a _k ± j b _k):

.

Поскольку для устойчивой системы Re p_i= a _i <0 и Re p_k= a _k <0, то все сомножители в этой формуле будут иметь положительные коэффициенты. Отсюда следует необходимое условие устойчивости (теорема Стодолы):

· Для устойчивой системы все коэффициенты характеристического полинома устойчивой системы всегда имеют одинаковый знак (например, положительный).

Для ЛДС 1-го и 2-го порядка это необходимое условие устойчивости является еще и достаточным. В этом легко убедиться непосредственно, записав выражения для характеристических корней:

n =1; A (p)= a ₀ + a ₁ p; p ₁= – a ₀/ a ₁

Корень p ₁ будет отрицательным только при одинаковых знаках коэффициентов a ₀ и a ₁ (например, при положительных).

n =2; A (p)= a ₀ + a ₁ p + a ₂ p ²; .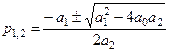

Для комплексных кор ней дискриминант должен быть отрицателен, что возможно только при одинаковых знаках a ₀ и a ₂. Если, кроме того, коэффициенты a ₁ и a ₂ одинаковы по знаку, то Re p_1,2 = – a ₁/(2 a ₂) < 0.

Для вещественных корней при одинаковых знаках a ₀ и a ₂ дискриминант будет неотрицателен, а по величине меньше, чем | a ₁|. Поэтому он не влияет на знак числителя и тогда при одинаковых знаках a ₁ и a ₂ оба корня p _1,2<0.

Если порядок ЛДС выше второго, то совпадения знаков коэффициентов характеристического уравнения (или полинома) недостаточно для ее устойчивости, а требуется выполнение некоторых дополнительных условий. Они устанавливаются необходимыми и достаточными критериями устойчивости.

б) критерий устойчивости Рауса (1877 г.). Этот критерий является необходимым и достаточным и имеет табличную форму. По известным коэффициентам характеристического уравнения по специальному правилу (алгоритму Рауса) заполняется таблица, которая имеет n +1 строку, N основных столбцов и один вспомогательный столбец. При этом, если n - четное число, то N =(n +2)/2, а для нечетного n число столбцов N =(n +1)/2.

Таблица Рауса имеет следующий вид:

-	r 11 =an	r 12 =an -2	…	r 1 N
-	r 21 =an -1	r 22 =an -3	…	r 2 N
l3=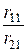	r 31= r 12- l3 r 22	r 32= r 13- l3 r 23	…
l4=	r 41= r 22- l4 r 32	r 42= r 23- l4 r 33	…
…	…	…	…
l n	rn1	…	…
l n+1	rn +1,1	…	…

Эта таблица заполняется построчно слева направо. В первых двух строках записываются коэффициенты характеристического полинома, начиная со старшего. Отсутствующие коэффициенты считаются нулевыми. Заполнение остальных строк (i ³ 3) начинается с определения элемента нулевого столбца l _i = r_{i -2,1}/ r_{i -1,1}, который равен отношению элементов первого основного столбца из двух предыдущих строк (например, l₃= r ₁₁/ r ₂₁).

Остальные элементы текущей строки заполняются по следующему правилу: r_ij = r_{i - 2,j+1} -l _i r_{i - 2,j+1}, где используются элементы соседнего справа столбца из двух предыдущих строк (например, r ₃₁= r ₁₂- l₃ r ₂₂). При этом элементы с несуществующими индексами принимаются равными нулю.

Критерий устойчивости Рауса формулируется следующим образом.

· Для того чтобы ЛДС была устойчивой, необходимо и достаточно, чтобы все элементы первого основного столбца таблицы были строго положительны.

В противном случае ЛДС либо не устойчива, либо находится на границе устойчивости. Число перемен знака в первом столбце равно количеству неустойчивых, т.е. расположенных в ППП, корней.

У этого критерия есть два полезных следствия, которые удобно использовать для построения границ устойчивости:

1) Если последний элемент 1-го столбца равен нулю (r_{n +1,1}=0), а все остальные положительны, то система имеет один нулевой корень и находится на апериодической границе устойчивости.

2) Если предпоследний элемент 1-го столбца равен нулю (r_n =0), а все остальные положительны, то ЛДС имеет два корня на мнимой оси и находится на колебательной границе устойчивости.

Критерий легко программируется, поэтому с помощью его можно проверить устойчивость ЛДС на множестве узлов сетки, покрывающей плоскость некоторых двух ее параметров. Те узлы, в которых ЛДС устойчива, принадлежат области устойчивости. Эта идея положена в основу сеточного метода построения области устойчивости. Аналогично можно приближенно отыскать такие узлы сетки, для которых система будет иметь одно и то же количество правых корней. Такие области называются D-областями. Среди них область устойчивости - это такая область, точкам которой соответствует нулевое количество правых корней.

Для систем по четвертый порядок включительно, таблицу легко заполнить при буквенных обозначениях коэффициентов характеристического уравнения и, следовательно, можно получить аналитические условия (уравнения) для построения колебательной и апериодической границ устойчивости.

Пример 1. С помощью критерия Рауса исследовать устойчивость системы третьего порядка и получить условия границ устойчивости.

Запишем характеристическое уравнение ЛДС при n =3 в общем виде:

A (p)= a ₀ + a ₁ p + a ₂ p ² + a ₃ p ³=0.

Составим таблицу Рауса и применим критерий и его следствия.

-	r 11 =a3	r 12 =a 1
-	r 21 =a 2	r 22 =a0
l3=	r 31= a 1- l3 a 0
l4=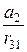	r 41= a 0

Условия устойчивости:

a₃> 0; a ₂>0; a ₁- l₃ a ₀= a ₁- a ₀>0; a ₀>0. А так как l₃= a ₃/ a ₂>0, то и a ₁>0.

Отсюда следует, что при условии положительности коэффициентов, для устойчивости системы 3-го порядка необходимо и достаточно, чтобы a ₁ a ₂- a ₀ a ₃>0.

Условие апериодической границы: a ₀=0 при a ₁>0; a ₂>0; a ₃>0; a ₁ a ₂- a ₀ a ₃> 0.

Условие колебательной границы: a ₁ a ₂- a ₀ a ₃= 0 при a ₀>0; a ₁>0; a ₂>0; a ₃>0.

Формально, этот критерий можно применить к «обращенному» полиному, для которого p =. Коэффициенты этого полинома нумеруются в обратной последовательности: .

Знаки корней и условия устойчивости для «прямого» и обращенного полиномов одинаковы, а корни их взаимно обратные. Поэтому условие нулевого корня для исходного полинома будет условием для бесконечного корня для обращенного полинома и наоборот. Условие нулевого корня для обращенного полинома a_n =0 – это условие для бесконечного корня исходного полинома. Поэтому условие апериодической границы для этого полинома будет условием такой же границы для бесконечного корня.

Применим полученные выше результаты для исследования устойчивости одноконтурной САР с передаточной функцией разомкнутого контура

.

Найдем характеристический полином для замкнутой системы A (p):

A (p)= K + p +(T ₁+ T ₂) p ²+ T ₁ T ₂ p ³.

Система будет устойчива при К, T ₁, T ₂ >0, если T ₁+ T ₂ > KT ₁ T ₂.

Апериодическая граница устойчивости (нулевой корень при двух других корнях в ЛПП) будет при K =0.

Колебательная граница устойчивости (два мнимых корня при отрицательном третьем корне) будет, если T ₁>0 и T ₂>0, а T ₁+ T ₂ = KT ₁ T ₂

Уравнение для колебательной границы области устойчивости в плоскости параметров T ₁ и T ₂ будет иметь вид:

.

Область устойчивости - это часть первого квадранта, расположенная ниже этой границы. Положительные полуоси координат представляют собой апериодические границы области устойчивости и соответствуют удаленному в минус бесконечность вещественному корню. При этом происходит понижение порядка системы на единицу, а два другие корня являются устойчивыми и могут быть либо комплексными (при T ₁+ T ₂>1/ K), либо вещественными.

Более наглядно и просто область устойчивости можно изобразить на плоскости частот сопряжения w₁=1/ T ₁ и w₂=1/ T ₂. С этой целью перепишем уравнение для колебательной границы устойчивости в виде: w₁+ w₂= K. Тогда граница области будет отрезок прямой, отсекающей по осям координат отрезки длиной " К " и расположенный в первой четверти. Оси координат соответствуют границе, когда два корня в начале координат, а один - вещественный отрицательный.

в)критерий устойчивости Гурвица (1895 г.). Этот критерий имеет аналитическую форму и более удобен в применении. Здесь предварительно составляется матрица Гурвица размером nxn по следующему правилу: вектор коэффициентов (a_n–1, a_n–2, …, a ₂, a ₁, a ₀) располагается по главной диагонали, а затем заполняется нижний треугольник матрицы по столбцам (вниз от диагонального элемента) в порядке возрастания индексов коэффициентов. Верхний треугольник заполняется аналогично, но вверх от диагонали и в порядке убывания индексов. Элементы с несуществующими индексами равны нулю.

Затем для полученной матрицы записываются и вычисляются все главные диагональные миноры D₁, D₂, D₃, …, D _{n -1}, D _n. Если все эти миноры (определители Гурвица) положительны, то ЛДЗ устойчиво. В противном случае оно либо неустойчиво, либо на границе устойчивости. Колебательной границе соответствует, при всех a_i >0 и положительных минорах D₁, D₂, D₃, …, D _{n -2}, условие D _{n -1}=0.

Апериодической границе устойчивости соответствует, при положительных минорах D₁, D₂, D₃, …, D _{n -1}, условие a ₀=0.

Эти граничные условия удобно использовать при определении областей устойчивости замкнутых САР в плоскости каких-либо двух параметров системы g₁ и g₂.

Критерий Льенара-Шипара, по сути, является модификацией критерия Гурвица: при a_i >0 (i =0, 1, …, n) для устойчивости ЛДЗ c четным n требуется положительность определителей Гурвица нечетных порядков, а для нечетного n, положительность определителей четных порядков.

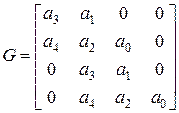; D₄= a ₀D₃; ; ; D₁ = a ₃;

Условия устойчивости при n =4 примут следующий вид:

D₄= a ₀D₃>0; D₃ = a ₁D₂- a ₀= a ₁(a ₂ a ₃- a ₁ a ₄) - a ₀>0; D₂= a ₂ a ₃- a ₁ a ₄>0; D₁= a ₃>0.

Легко заметить, что при D₃>0, D₂ и D₄ тоже положительны. Следовательно, при положительных коэффициентах необходимое и достаточное условие устойчивости запишется так:

a ₁(a ₂ a ₃- a ₁ a ₄) - a ₀>0.

Условие апериодической границы:

a ₀=0 при a ₁>0; a ₂>0; a ₃>0; a ₄>0; a ₁(a ₂ a ₃- a ₁ a ₄) - a ₀>0.

Условие колебательной границы:

a ₁(a ₂ a ₃- a ₁ a ₄) - a ₀=0 при a ₀>0; a ₁>0; a ₂>0; a ₃>0; a ₄>0.

Позднее, в 1914 г. Льенаром и Шипаром было показано, что для суждения об устойчивости ЛДС при положительных коэффициентах достаточно проверять не все миноры, а только D _{n –1}, D _{n –3}, D _{n –5},.... Положительность остальных миноров обеспечивается автоматически.

Дата добавления: 2014-01-11