Алгебраический матричный критерий устойчивости

(критерий Зубова)

В тех случаях, когда исследуемая САУ имеет высокий порядок (десятки и более) и известны уравнения состояния с матрицей A, то исследовать ее устойчивость можно не зная коэффициентов характеристического полинома A (p)=det[ p E – A ]. Это тем более важно, поскольку для систем высокого порядка эта процедура связана с вычислительными трудностями (в смысле точности определения этих коэффициентов). В критерии устойчивости Зубова используется матрица A _x =[ E + A ][ E – A ]^–1= E +2 A [ E – A ]^–1. Согласно этому критерию, для устойчивости САР необходимо и достаточно, чтобы степень матрицы A _x стремилась к нулевой матрице:

. (1)

Показать справедливость этого критерия можно, если в характеристическом уравнении det[ p E – A ]=0 от переменной Лапласа p с помощью дробно-линейной подстановки перейти к новой комплексной переменной r:

r = (1+ p)/(1– p) и p =(r–1)/(r+1).

Особенность такой подстановки в том, что левая полуплоскость переменной p отображается во внутреннюю часть единичного круга плоскости r, а поэтому условие устойчивости для корней преобразованного характеристического уравнения det[ r E – A ]=0 будет иметь вид |r _i |< 1.

Убедимся в этом, рассмотрев модуль одного из корней:

|r _i |=.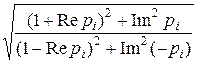

Отсюда следует, что если Re p_i <0, то |r _i |< 1 и наоборот, |r _i |>1 при Re p_i >0.

Далее, выполнив в det(p E – A)=0 указанную выше замену переменной, после ряда эквивалентных преобразований получим «новое» характеристическое уравнение:

|r E – [ E + A ][ E – A ]^–1| = 0 или |r E– ­­­ A _x |=0.

Пусть, для простоты, все корни r _i некратные. В этом случае матрица A _x неособым преобразованием приводится к диагональному виду, где по диагонали располагаются корни r _i. Тогда (A _x) ^k будет эквивалентна диагональной матрице diag{(r _i) ^k }. Если для всех |r _i |<1, то при увеличении k матрица (A _x) ^k будет стремиться к нулевой матрице.

При практическом использовании критерий Зубова применяется либо в необходимой, либо в достаточной форме:

1. Если САР устойчива, то след матрицы Sp A _x меньше порядка матрицы n.

Тогда при Sp A _x > n САР будет неустойчивой.

2. Если норма (любая) матрицы A _x или некоторой степени k этой матрицы

меньше единицы, то ЛДС устойчива.

3. Если следы некоторых трех последовательных степеней матрицы A _x

образуют убывающую последовательность, то ЛДС устойчива.

Метод исследования устойчивости на основе матричного критерия Зубова ориентирован исключительно на компьютерные вычисления. При этом предполагается, что имеется хороший вычислительный алгоритм нахождения обратной матрицы высокого порядка.

Дата добавления: 2014-01-11