Метод Карно

ЛЕКЦИЯ 2.

Карта Карно представляет собой прямоугольную таблицу, количество клеток в которой равно 2ⁿ, где n – число логических переменных минимизируемой логической функции.

Минимизация с помощью карт Карно наглядна при количестве логических переменных меньше или равно 4. Если n>4, то ситуация несколько усложняется и минимизацию проводят, как правило, при помощи компьютеров.

Рассмотрим процесс минимизации, полагая n=4, т.е. для y(a, b, c, d). Карта Карно для четырех переменных состоит из 16 клеток. По строкам будем менять значение переменных a и b, а по столбцам с и d.

Для минимизации логической функции y(a, b, c, d), прежде всего, необходимо представить её в СДНФ.

Рассмотрим в качестве примера минимизацию следующей логической функции: .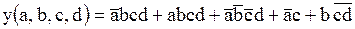

1. Приведем данную логическую функцию к нормальной форме, т.е.

преобразуем исходное выражение к следующему виду:

.

Т.о., используя правило де'Моргана и раскрывая скобки в последнем слагаемом, мы избавились от отрицания над несколькими переменными, и пришли к ДНФ.

2. Далее, приведем, полученную в предыдущем пункте, ДНФ к совершенной

форме. Для этого используем правило 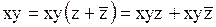для тех слагаемых, в которых отсутствуют какие-либо переменные. Поскольку 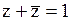, то очевидно, что умножение xy на 1 не меняет значения логической функции.

Итак,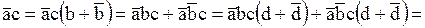

.

.

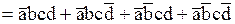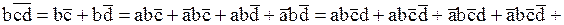
В результате проведенных преобразований исходная логическая функция будет представлена в СДНФ:

.

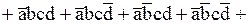
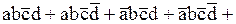
После приведения подобных, получаем:

.

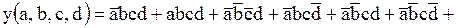
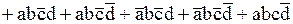3. Поскольку заданная логическая функция представлена

теперь в СДНФ, то можно заполнить карту Карно:

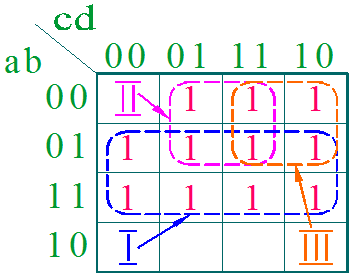
Для этого в клетки карты, соответствующие слагаемым, представленной для минимизации, функции, записываются единицы.

4. Особо следует остановиться на процессе организации

склеек.

Значения переменных в соседних клетках карты, как по строкам, так и по столбцам, отличаются значением только одной переменной (так организована карта). Кроме того, крайние клетки в строках и столбцах, так же, отличаются значением только одной переменной и называются соседними. Такая организация карты необходима для того, чтобы организовать закон склейки – 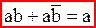. Т.о. если взять две единицы в соседних клетках и склеить их по меняющейся переменной, то получим одно слагаемое минимизированной логической функции в виде произведения переменных, не меняющих свое значение в пределах этих двух клеток.

Склейкой называется объединение 2^k клеток, где k=0, 1, 2, …, n, где n – количество входных переменных.

При организации склеек необходимо исходить из следующих правил:

I. Форма склейки может быть только прямоугольной, причем в одну склейку,

как уже было указано, может входить лишь количество клеток равное 2^k. Кроме того, единицы, расположенные в крайних или угловых клетках, могут склеиваться по строкам и (или) по столбцам с единицами, расположенными в соседних (т.е. находящихся с другой стороны карты) клетках, если таковые имеются.

В приведенном примере самой большой склейкой является склейка из восьми клеток (склейка ).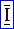

II. Одна и та же клетка может участвовать в нескольких склейках. Это имеет

смысл в том случае, если удается тем самым увеличить размер склейки.

III. В процессе формирования склеек необходимо стремиться к образованию

склеек максимально возможного размера.

IV. Количество склеек должно быть минимальным, однако, склейками должны

быть охвачены все единицы, имеющиеся в карте.

Каждая из склеек формирует слагаемое минимизированной функции. Получается это слагаемое следующим образом. В пределах склейки определяются те логические переменные, которые не меняют своего значения. Т.о., в рассматриваемом примере, первая склейка дает слагаемое "b", вторая склейка – 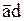и третья – 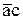. В результате получаем минимизированную форму записи исходной функции в следующем виде:

.

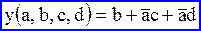Из полученного в примере результата видно, что чем крупнее склейка, тем меньше сомножителей в соответствующем слагаемом. Если какая-либо клетка не входит ни в одну из склеек, т.е. при k=0, то слагаемое, находящееся в этой клетке, переписывается без изменений.

Рассмотрим еще один пример. Предположим, что исходная логическая функция имеет следующий вид:

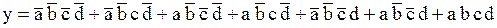. Заполняем карту Карно

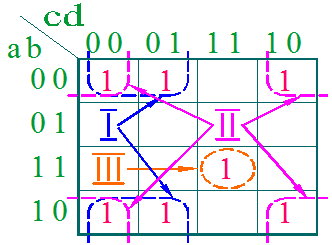
В данном случае можно провести три склейки, следовательно, минимизированная функция будет содержать три слагаемых:

.

.

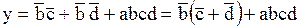Существует класс логических функций, которые называются недоопределенными. Недоопределенные функции это такие логические функции, для которых существуют запрещенные комбинации входных переменных, т.е. такие логические комбинации, которые не могут появиться на входе ни при каких обстоятельствах.

Например, при преобразовании двоичного кода в десятичный. Для представления десятичных цифр в двоичном коде необходимо четыре разряда. Поэтому при заполнении таблицы истинности, соответствующей такому преобразованию, таблица будет содержать шестнадцать строк, из которых будут использоваться только первые десять. Остальные шесть строк использоваться не будут, т.е. при схемной реализации такого преобразователя эти шесть входных комбинаций никогда не появятся на входе. Т.о. эти последние шесть комбинаций для такого преобразования являются запрещенными.

При минимизации недоопределенных логических функций необходимо учитывать эти запрещенные состояния, поскольку это позволяет дополнительно упростить минимизированную функцию.

Предположим, что в рассмотренном выше примере существует три запрещенных состояния: .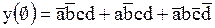

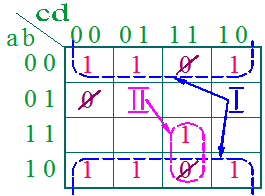
Внесем эти запрещенные состояния в карту Карно.

При минимизации клетки с запрещенными состояниями проектировщик вправе по своему усмотрению принимать как за ноль, так и за единицу. При этом, единственным критерием выбора является увеличение размеров склеек и уменьшение их числа.

В рассматриваемом примере эту задачу можно решить, если два запрещенных состояния принять за единицу, а одно – за ноль, как показано на приведенном рисунке. Тогда, при организации склеек, получаем одну склейку из восьми клеток и одну склейку из двух. И минимизация исходной логической функции, с учетом запрещенных состояний, приводит к следующему результату:

.

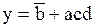Т.о. одна и та же исходная логическая функция при минимизации может быть существенно упрощена, если учитывать запрещенные состояния.

Однако, учет запрещенных состояний не всегда упрощает минимизированную логическую функцию.

Все предыдущее рассмотрение справедливо только в том случае, если количество входных переменных "n" не превышает четырех. В противном случае процесс минимизации с помощью карт Карно существенно усложняется.

Рассмотрим, в качестве примера, случай, когда имеются пять входных переменных. Для этого разместим рядом две карты Карно для четырех переменных, одна карта для переменной f, а другая – для 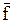, как показано на следующем рисунке:

		×
	×		×
		×

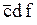
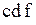
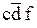
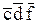
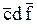
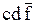
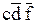
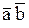
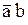
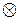
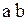
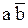
В такой карте организация склеек усложняется, поскольку для клетки, в которой на рисунке помещена единица, соседними являются не только клетки с крестиками, но и клетка, в которой находится крестик в кружочке.

Поскольку при организации склеек в случае, когда количество входных переменных больше четырех, требуется учитывать все соседние клетки для каждого слагаемого, которые оказываются разбросанными по всей карте, то минимизацию проводят с применением вычислительной техники. Однако принцип проведения минимизации остается таким же, как и для случая, когда n≤4.

В литературе часто встречается аналог карты Карно, который носит название метода диаграмм Вейча.

После получения минимизированной логической функции можно приступить к этапу её физической реализации на цифровых логических элементах.

Дата добавления: 2014-01-11