Минимизация логических функций

Существует несколько методов минимизации (упрощения) формул логических функций. Сама процедура минимизации проводится с целью получения простейшей записи, при аппаратурной реализации которой полученная схема отличалась бы минимальным количеством логических элементов, а, следовательно, и стоимостью. Общих методов, позволяющих с помощью стандартных приемов получить простейшую запись формул, не существует. Разработаны несколько методов, которые позволяют это делать при наличии определенных навыков. Одним из возможных методов является метод, который заключается в последовательном преобразовании логических функций, пользуясь правилами алгебры логики (чаще всего правилами поглощения и склейки).

Пример: минимизировать следующую логическую функцию: .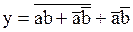

Для минимизации этой функции необходимо применить правило, которое является общим для всех методов минимизации, правило Де–Моргана, поскольку имеется общее отрицание над несколькими переменными. Т.о. получаем следующее выражение:

.

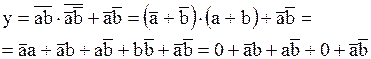Согласно комбинационному закону 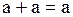, к полученному результату можно прибавить 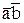, без изменения общего значения функции. Тогда:

.

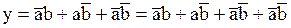Полученная запись может быть преобразована далее, согласно закону склейки:

.

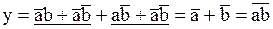Если бы к первоначальному результату не было дописано дополнительное слагаемое 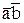, то решение имело бы следующий вид:

.

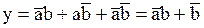Далее, согласно дистрибутивному закону, получаем следующий результат:

.

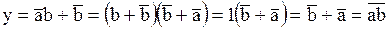Использование такого приема, однако, может, иногда, приводить к тупиковым формулам, которые логически эквивалентны исходным выражениям, однако, переход от одного к другому невозможен. Простейшая форма записи любой логической функции, в частности, является тупиковой формулой. Например:

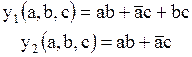
Эти две формулы логически абсолютно эквивалентны, хотя переход из одной в другую оказывается невозможным. Эквивалентность приведенных функций можно проверить при помощи следующей таблицы истинности.

A	B	C	y1	y2

Для минимизации логических функций, при ограниченном количестве переменных, существуют стандартные методы минимизации.

Дата добавления: 2014-01-11