
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пам'ятка
|
|
|
|
1.Перевіряю: чи можна з одиниць зменшуваного відняти одиниці від'ємника:
Так Ні
2.Заміняю зменшуване сумою
розрядних зручних
доданків
3. Віднімаю десятки.
4. Віднімаю одиниці.
5. Додаю отримані різниці.







 Наприклад: 56 – 34 = 50 + 6 – 30 - 4 = 16 + 6 = 22 56 – 38 = 40 + 16 – 30 - 8 = 10 + 8 = 18
Наприклад: 56 – 34 = 50 + 6 – 30 - 4 = 16 + 6 = 22 56 – 38 = 40 + 16 – 30 - 8 = 10 + 8 = 18
50+6 30+4 40+16 30+8
Множення одноцифрового числа на двоцифрове число та двоцифрового числа на одноцифрове.
Теоретична основа: правило множення суми на число.
Пам’ятка
|
|
3.Додаю отримані результати.
4.Читаю (записую) відповідь.
Ділення двоцифрового числа на одноцифрове, коли ділене замінюють сумою зручних доданків
Теоретична основа: правило ділення суми на число.
|
|
 1.Подаю ділене у вигляді суми розрядних (зручних) доданків.
1.Подаю ділене у вигляді суми розрядних (зручних) доданків.
2.Ділю кожний доданок на дільник.
3.Додаю отримані частки.
4.Записую (читаю) відповідь.
Ділення на двоцифрове число. Спосіб послідовного ділення
Теоретична основа: правило ділення числа на добуток.
|
1.
|
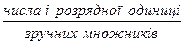 ;
;
2.
|
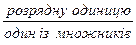 .
.
3. Ділю одержаний результат на інший множник.
4. Читаю (записую) відповідь.
Письмове додавання і віднімання.
Теоретична основа: правило додавання суми до суми та віднімання суми від суми.
Пам’ятка
- Підписую числа стовпчиком – розряд під розрядом.
- Виконувати дії починаю з розряду одиниць. Пам’ятаю, що 10 одиниць нижчого розряду складають 1 одиницю вищого.
- Виконую дії по розрядах.
- Читаю відповідь.
Письмове множення на одноцифрове число.
Теоретична основа: правило множення числа на суму.
Пам’ятка:
- Підписую числа стовпчиком: другий множник пишу під одиницями першого множника.
- Множення починаю з розряду одиниць. Множу одиниці першого множника на другий множник. Отримую одиниці. Результат записую під одиницями.
- Перехожу до множення десятків. Множу десятки першого множника на другий множник. Отримую десятки. Результат записую під десятками.
- Перехожу до множення сотень. Множу сотні першого множника на другий множник. Отримую сотні. Результат записую під сотнями.
І так далі...
- Читаю значення добутку.
Письмове множення на двоцифрове число.
Теоретична основа: правило множення суми на суму.
Пам’ятка
- Підписуємо множники стовпчиком.
- Множення починаємо з одиниць. Множимо одиниці другого множника на перший множник. Отримаємо одиниці – це 1 неповний добуток. Результат починаємо записувати з розряду одиниць.
- Множимо десятки другого множника на перший множник. Отримаємо десятки – це ІІ неповний добуток. Результат починаємо писати під десятками.
І так далі …
- Додаємо неповні добутки, отримуємо добуток.
Письмове ділення.
Теоретична основа: правило ділення суми на число.
1.Відділяю ділене від дільника куточком.
2.Визначаю 1-ше неповне ділене.
3.Визначаю найвищій розряд частки.
4.Визначаю кількість цифр в частці.
5.Ділю 1-ше неповне ділене на дільник. Записую 1-шу цифру частки.
6.Визначаю скільки одиниць даного розряду розділилися.
7.Визначаю скільки одиниць даного розряду не розділилося.
8.Перевіряю чи вірно знайдена цифра частки.
9.Утворюю наступне неповне ділене.
10.Ділю наступне неповне ділене на дільник. Записую наступну цифру частки.
І так далі...
3. Прийоми, теоретична основа яких – зв’язки між компонентами і результатами арифметичних дій.
До них М.О.Бантова відносить прийми для випадків виду 9 – 7, 21: 3, 60: 20, 54: 18, 9: 1, 0: 6, зазначаючи, що при введенні цих прийомів спочатку розглядаються зв’язки між компонентами і результатами відповідної арифметичної дії, потім на цій підставі вводиться обчислювальний прийом.
До цього класу ми вслід за М.О.Бантовою відносимо наступні обчислювальні прийоми:
1) віднімання на підставі взаємозв’язку дій додавання і віднімання (9 – 7, 14 – 8);
2) ділення на підставі взаємозв’язку дій множення і ділення (21: 3, 51: 17, 60: 20);
3) ділення на 1;
4) ділення 0 на число;
5) ділення рівних чисел.
Віднімання на підставі взаємозв’язку дій додавання і віднімання.



 Наприклад: 9 - 6 = 3 + 6 – 6 = 3
Наприклад: 9 - 6 = 3 + 6 – 6 = 3
3+6
Ділення на підставі взаємозв’язку між множенням і діленням.
Пам’ятка
- Подаю ділене у вигляді добутку двох множників.
- Якщо добуток двох множників поділити на один з них, то залишиться інший множник.
- Записую (читаю) відповідь.
Наприклад: 12: 3 = (4 * 3): 3 = 4 60: 20 = (3 * 20): 20 = 3
Спосіб випробування з прикидкою.
Пам’ятка
- Розділити число а на число в, означає знайти таке число с, яке при множенні на дільник в, дає ділене а.
 а: в = с, тому що с * в = а
а: в = с, тому що с * в = а
*
- Це число будемо знаходити випробуванням, застосовуючи прикидку:
- шукаю таке число, яке при множенні на одиниці дільника дає одиниці діленого; записую його;
- думаю, чи є ще такі числа; записую їх.
- випробую множенням всі записані числа.
- Роблю висновок.
 |

 Наприклад: 6 4: 16 =, * 16 = 64
Наприклад: 6 4: 16 =, * 16 = 64
*
4, 9
4 * 16 = 64, 64 = 64
64: 16 = 4, тому що 4 * 16 = 64
Ділення на 1.Ділення рівних чисел

1 . а = а

а: 1 = а При діленні будь-якого числа на одиницю
 в частці отримаємо те саме число.
в частці отримаємо те саме число.
а: а = 1
При діленні будь-якого числа на себе
в частці отримаємо одиницю.
Ділення нуля.

0 . а = 0

0: 1 = 0 При діленні нуля на будь-яке число
 в ча стці отримаємо нуль. На нуль ділити
в ча стці отримаємо нуль. На нуль ділити
0: 0 - не не можна!
можна!
2. Прийоми, теоретична основа яких – змінення результатів арифметичних дій в залежності від зміни одного з компонентів.
Це прийоми округлення при виконанні додавання і віднімання чисел (46 + 19, 512 – 298) і прийоми множення і ділення на 5, 25, 50. Введення цих прийомів також вимагає попереднього вивчення відповідних залежностей.
Наприклад:
24 + 78 = 24 + 80 – 2 = 104 – 2 = 102
Тут ми застосовуємо правило: якщо один із доданків збільшиться на 2, то й сума збільшиться на 2. Тому, щоб сума не змінилася, треба від отриманого результату відняти 2.
56 – 37 = 56 – 40 + 3 =16 + 3 = 19
Тут застосовуємо таке правило: якщо від’ємник збільшити на 3, то різниця зменшиться на 3. Тому, щоб різниця не змінилася, треба до отриманого результату додати 3.
36 * 5 = 36 * 10: 2 = 360: 2 = 180
Тут застосовуємо правило: якщо один із множників збільшити в 2 рази, то й добуток збільшиться в 2 рази. Тому, щоб добуток не змінився, треба отриманий результат поділити на 2.
Аналогічно: 36 * 50 = 36 * 100: 2 = 3600: 2 = 1800
36 * 500 = 36 * 1000: 2 = 36000: 2 = 18000
Якщо ділене закінчується нулями, то аналогічно можна виконувати ділення на 5, 50, 500:
620: 5 = 620: 10 * 2 = 62 * 2 = 124
Тут застосовуємо правило: якщо дільник збільшити в 2 рази, то частка зменшиться в 2 рази. Тому, щоб частка лишилася незмінною, треба отриманий результат помножити на 2.
Аналогічно: 1300: 50 = 1300: 100 * 2 = 13 * 2 = 26
83000: 500 = 83000: 1000 * 2 = 83 * 2 = 166
Але, цей прийом можна застосовувати не для всіх випадків, а лише тоді, коли в дільнику є достатня кількість нулів, щоб його поділити на розрядну одиницю.
Так само розглядається множення і ділення на 25, 250:
32 * 25 = 32 * 100: 4 = 3200: 4 = 800
56 * 250 = 56 * 1000: 4 = 56000: 4 = 12000
Тут застосовується правило: якщо один із множників збільшити в 4 рази, то й добуток збільшиться в 4 рази. Для того, щоб добуток не змінився треба отриманий результат зменшити в 4 рази.
Виконувати множення таким способом можна в будь-якому випадку; тому що при множенні його на 100 (1000), отримаємо число дві останні цифри якого створюють число, що ділиться на 4. Але треба підбирати такий перший множник, щоб отриманий результат можна було усно поділити на 4.
При діленні на 25, 250 слід мати на увазі, що ділене повинно закінчуватися достатньою кількістю нулів:
3100: 25 = 31: 100 * 4 = 31 * 4 = 124
76000: 250 = 76000: 1000 * 4 = 76 * 4 = 304
Тут застосовується правило: якщо дільник збільшимо в 4 рази, то частка зменшиться в 4 рази. Тому, щоб частка не змінилася треба результат збільшити в 4 рази.
При множенні на 25 можна міркувати і інакше:
32 * 25 = (32: 4) * (25 * 4) = 8 * 100 = 800
Тут застосовується правило: добуток не змінюється, якщо один множник зменшити в 4 рази, а інший, навпаки, збільшити в 4 рази. Але, в цьому випадку слід підбирати такий множник, що ділитиметься на 4.
Вже в початковій школі, учні повинні засвоїти такі правила:
1. Якщо один із доданків 
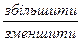 на декілька одиниць, в інший доданок залишити без змін, то сума
на декілька одиниць, в інший доданок залишити без змін, то сума 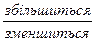 на стільки ж одиниць.
на стільки ж одиниць.
2. Якщо один із множників 
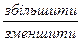 в декілька разів, в інший множник залишити без змін, то добуток
в декілька разів, в інший множник залишити без змін, то добуток 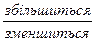 у стільки ж разів.
у стільки ж разів.
3. Якщо один доданок 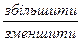 на декілька одиниць, а інший доданок, навпаки,
на декілька одиниць, а інший доданок, навпаки, 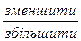 на стільки ж одиниць, то сума лишиться не змінною.
на стільки ж одиниць, то сума лишиться не змінною.
4. Якщо один множник 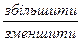 в декілька разів, а інший множник, навпаки,
в декілька разів, а інший множник, навпаки, 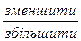 у стільки ж разів, то добуток лишиться не змінним.
у стільки ж разів, то добуток лишиться не змінним.
5. Якщо зменшуване 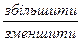 на декілька одиниць, а від’ємник залишити без змін, то різниця
на декілька одиниць, а від’ємник залишити без змін, то різниця 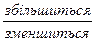 на стільки ж одиниць.
на стільки ж одиниць.
6. Якщо ділене 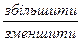 в декілька разів, а дільник залишити без змін, то частка
в декілька разів, а дільник залишити без змін, то частка 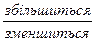 у стільки ж разів.
у стільки ж разів.
7. Якщо від’ємник 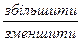 на декілька одиниць, а зменшуване залишити без змін, то різниця, навпаки,
на декілька одиниць, а зменшуване залишити без змін, то різниця, навпаки, 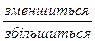 на стільки ж одиниць.
на стільки ж одиниць.
8. Якщо дільник 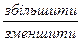 у декілька разів, а ділене залишити без змін, то частка, навпаки,
у декілька разів, а ділене залишити без змін, то частка, навпаки, 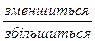 у стільки ж разів.
у стільки ж разів.
9. Якщо зменшуване 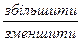 на декілька одиниць, а від’ємник також
на декілька одиниць, а від’ємник також 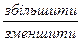 на стільки ж одиниць, то різниця не змініться.
на стільки ж одиниць, то різниця не змініться.
10. Якщо ділене 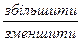 у декілька разів, а дільник також
у декілька разів, а дільник також 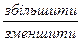 в стільки ж разів, то частка не змініться.
в стільки ж разів, то частка не змініться.
Прийом окрглення при додаванні і відніманні
Пам’ятка
Якщо 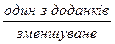 закінчується цифрою або 5, або 6, або 7, або 8, або 9, то
закінчується цифрою або 5, або 6, або 7, або 8, або 9, то
1. Замінюю його близьким круглим числом.
2. 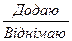 це кругле число.
це кругле число.
3. Дивлюся на скільки більше 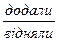 .
.
4. 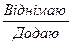 стільки ж одиниць.
стільки ж одиниць.
5. Читаю (записую) результат.

 Наприклад: 6 + 8 = 6 + 10 – 2 = 16 – 2 = 16 14 – 8 = 14 – 10 + 2 = 4 + 2 = 6
Наприклад: 6 + 8 = 6 + 10 – 2 = 16 – 2 = 16 14 – 8 = 14 – 10 + 2 = 4 + 2 = 6

 16 + 7 = 16 + 10 – 3 = 16 – 3 = 23 33 – 8 = 33 – 10 + 2 = 23 + 2 = 25
16 + 7 = 16 + 10 – 3 = 16 – 3 = 23 33 – 8 = 33 – 10 + 2 = 23 + 2 = 25
 26 + 35 = 30 + 35 – 4 = 65 – 4 = 61 76 – 38 = 76 – 40 + 2 = 36 + 2 = 38
26 + 35 = 30 + 35 – 4 = 65 – 4 = 61 76 – 38 = 76 – 40 + 2 = 36 + 2 = 38
Прийоми множення і ділення на 5, 50, 500
а * 5 = а * 10: 2 а: 5 = а: 10 * 2
а * 50 = а * 100: 2 а: 50 = а: 100 * 2
а * 500 = а * 1000: 2 а: 500 = а: 1000 * 2
Прийоми множення і ділення на 25, 250, 125
а * 25 = а * 100: 4 а: 25 = а: 100 * 4
а * 250 = а * 1000: 4 а: 250 = а: 1000 * 4
а * 125 = а * 1000: 8 а: 125 = а: 1000 * 4
2. Прийоми, теоретична основа яких – питання нумерації чисел.
До цього класу М.О.Бантова відносить прийоми для випадків виду а+ 1, а – 1, 10 + 6, 16 – 10, 16 – 6, 57 * 10, 1200: 100; аналогічні прийоми для більших чисел. Введення цих прийомів передбачається після вивчення відповідних питань нумерації (натуральної послідовності, десяткового складу чисел, позиційного принципу запису чисел).
Таким чином, в цей клас включимо обчислювальні прийоми:
1) додавання та віднімання числа 1;
2) додавання та віднімання на підставі десяткового складу чисел;
3) додавання і віднімання способом укрупнення розрядних одиниць;
4) множення та ділення на розрядну одиницю;
5) множення круглого числа на одноцифровея способом укрупнення розрядних одиниць;
6) ділення круглого числа на одноцифрове або ділення круглого числа на кругле способом укрупнення розрядних одиниць.
Додавання і віднімання числа 1.

Додавання та віднімання на підставі десяткового складу числа
Пам’ятка
- Визначаю десятковий склад першого числа.
- Визначаю, скільки одиниц і якого розряду треба
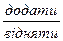 .
. - Об’єдную або вилучаю: “було”, “
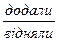 ”, “отримали”.
”, “отримали”. - Подаю одержане число у одиницях.
Наприклад: 50 + 6 = 5д.6од. = 56
74 – 70 = 7д.4од. – 7д. = 4од. = 4
68 – 8 = 6д.8од. – 8од. = 6д. = 60
Додавання та віднімання способом укрупнення розрядних одиниць
Пам’ятка
1. Замінюю кожне число однаковими більш круними розрядними одиницями.
2. 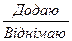 розрядні одиниці.
розрядні одиниці.
3. Подаю результат у одиницях.
Наприклад: 60 + 50 = 6 д. + 5 д. = 11 д. = 110 70 – 40 = 7 д. – 5д. = 2 д. = 20
60 + 80 = 6 д. + 8 д. = 14 д. = 140 110 – 40 = 11 д. – 4 д. = 7 д. = 70
180 + 230 = 18 д. + 23 д. = 41 д. = 410 340 – 260 = 34 д. – 26 д. = 8 д. = 80
600 + 240 = 60 д. + 24 д. = 84 д. = 840 700 – 550 = 70 д. – 55 д. = 15 д. = 150
3400 + 2700 = 34 с. + 27 с. = 61 с. = 6100 7400 – 2600 = 74 с. – 26 с. = 48 с. = 4800
Множення розрядної одиниці на число.
Пам’ятка
- Підраховую кількість нулів у розрядній одиниці.
- До даного числа праворуч приписую стільки ж нулів.
- Читаю отримане число.
Наприклад: 45 * 1 000 = 45 000
Ділення на розрядну одиницю
Пам’ятка
- Підраховую кількість нулів у розрядній одиниці.
- Від даного числа справа закриваю стільки ж нулів.
- Читаю отримане число.
Наприклад: 450 00 * 1 00 = 45
Множення або ділення круглого числа на одноцифрове способом укрупнення розрядних одиниць
Пам’ятка
- Замінюю кругле число більш крупними розрядними одиницями.
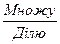 число розрядних одиниць на число, одержую результат у тих самих розрядних одиницях.
число розрядних одиниць на число, одержую результат у тих самих розрядних одиницях.- Подаю одержаний результат у одиницях.
Наприклад: 20 * 4 = 2 д. * 4 = 8 д. = 80 60: 3 = 6 д: 3 = 2 д. = 20
200 * 4 = 2 с. * 4 = 8 с. = 800 600: 3 = 6 с.: 3 = 2 с. = 200
120 * 3 = 12 д. * 3 = 36 д. = 360 720: 6 = 72 д.: 6 = 12 д. = 120
Ділення круглого числа на кругле способом укрупнення розрядних одиниць
Пам’ятка
- Замінюю ділене і дільник однаковими більш крупними розрядними одиницями.
- Ділю числа розрядних одиниць, одержую відлучене число.
Наприклад: 60: 20 = 6 д.: 2 д. = 3 600: 200 = 6 с.: 2 с. = 3
600: 20 = 60 д.: 2д. = 30 720: 60 = 72 д.: 6 д. = 12
6. Прийоми, теоретична основа яких – правила.
До них відносяться прийоми двох випадків: а * 1, а * 0. Оскільки, правила множення чисел на одиницю і нуль є наслідками з означення дій множення цілих невід’ємних чисел, то вони просто повідомляються і у відповідності з ними виконуються обчислення.
1. Правило множення будь-якого числа на одиницю: при множенні будь-якого числа на одиницю в добутку отримаємо теж саме число.
|
2. Правило множення будь-якого числа на нуль: при множенні будь-якого числа на нуль в добутку отримаємо нуль.
|
М.О.Бантова зазначає, що цілий ряд випадків може бути віднесений не лише до вказаної групи прийомів, але й до іншої. Наприклад, випадки виду 46 + 19 можна віднести не лише до четвертої групи, але й до другої. Це залежить від вибору теоретичної основи обчислювального прийому. Можливість використання різноманітних теоретичних положень при конструюванні обчислювальних прийомів для одного випадку обчислення (наприклад, для випадку додавання 46 + 19) є перед посилкою формування раціональних і гнучких обчислювальних навиків.
В таблиці 1 наведено розподіл випадків обчислень та відповідних прийоми обчислення по темах.
Таблиця 1.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 891; Нарушение авторских прав?; Мы поможем в написании вашей работы!