Напряжения растяжения от центробежных сил

Расчетная схема определения напряжений растяжения

представлена на следующем рисунке 5.5.

Рисунок 5.5

Выделяется элементарный участок бесконечно малой толщины dr.

Центробежная сила данного участка равна

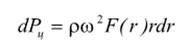
где ρ – плотность материала; ω — угловая скорость колеса; F - площадь поперечного сечения лопатки на радиусе г.

РАЗМЕРНОСТИ

Центробежная сила, действующая в произ­вольном сечении рабочей лопатки на радиусе R, определяется интегрированием:

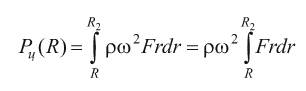
При наличии бандажной полки, имеющей объем V_n и расположенной на радиусе R_П, в сече­ниях пера с большим радиусом (R> R_П) появляет­ся дополнительная сила - центробежная сила пол­ки Р_П. Для ее вычисления полка представляется в виде сосредоточенной массы:

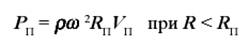
В рамках стержневой модели напряжения ра­стяжения равномерно распределены в поперечных сечениях пера лопатки. Напряжения растяжения σ_р (R) в произвольном сечении с радиусом R опре­деляются как отношение силы к площади сечения

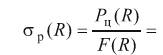
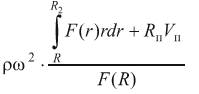
Второе слагаемое в числителе – для лопаток с полкой при R < R _П.

Площадь F поперечного сечения лопатки изменяется по ее длине по разным законам. Частные случаи.

а) Лопатка постоянного поперечного сечения

F(R) = const = F (без полки)

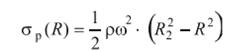
В лопатках постоянного поперечного сече­ния имеет место самое высокое напряжение рас­тяжения по сравнению с другими использующи­мися законами распределения площадей. Поэтому они применяются лишь в ненагруженных ступе­нях двигателей при малых размерах лопатки, ког­да основными становятся соображения техноло­гичности.

б) Лопатка со степенным законом изменения площади сечения по высоте. В таких лопатках пло­щадь поперечного сечения лопатки изменяется по закону

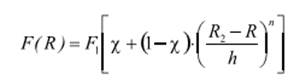
Лопатки со степенным законом изменения площади позволяют минимизировать величину напряжений растяжения (рисунок 5.6 – χ = 0,3).

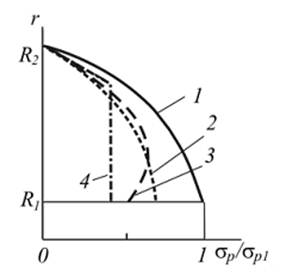
Рисунок 5.6

Наименьшее значение максимального напряжения получается при 2 < п < 3. Следует подчеркнуть, что снижение массы лопаток, достигаемое при рациональном профилировании, приводит, также, и к снижению массы дисков. Кривая 4 соответствует равнопрочным лопаткам при действии только ЦБ сил (на практике не применяется – нужен учет газовых сил и т.д.).

На следующем рисунке 5.7 показано распределение напряжений

для случаев, когда полка расположена на конце ло­патки (кривая 1) и в средней части пера (кривая 2).

Кривая 1 – полка (бандажная) расположена на концевой части лопатки

Кривая 2– полка (антивибрационная) расположена в средней части

Рисунок 5.7

Заметим, что напряжения возрастают только в той части пера, которая находится ниже полки.

Дата добавления: 2014-01-11