Если несколько простых высказываний объединены в одно с помощью логических операций и скобок, то такое высказывание называется сложным

Простым называется высказывание, которое не содержит в себе других высказываний.

ЛОГИЧЕСКИЕ ПЕРЕМЕННЫЕ И ЛОГИЧЕСКИЕ ФУНКЦИИ

Буквы, обозначающие высказывания (А, В, …), можно рассматривать как имена логических переменных, так как ими можно заменить любые высказывания (с любым содержанием). Логические переменные принимают два значения: 0 и 1 («истина» и «ложь»). В алгебре логики из логических переменных, логических констант (0 и 1), знаков логических операций и скобок составляются логические выражения (подобно тому, как в алгебре чисел формируются арифметические выражения).

Логическое выражение (логическая форма) – это выражение, содержащее одну или несколько переменных, соединенных знаками логических операций и скобками и превращающихся в высказывания при подстановке вместо этих переменных простых суждений.

Выражения алгебры логики также называют формулами.

Логическая функция – это функция, определенная на множестве истинностных значений (истина, ложь) и принимающая значение из того же множества.

Высказывания бывают простые и сложные.

Примеры простых высказываний: 1) Идет дождь; 2) Студентам живется весело.

Скобки необходимы для определения порядка выполнения логических операций. Примеры сложных высказываний:

СЛОЖНОЕ ВЫСКАЗЫВАНИЕ	СОСТАВЛЯЮЩИЕ ПРОСТЫЕ ВЫСКАЗЫВАНИЯ	ФОРМА СЛОЖНОГО ВЫСКАЗЫВАНИЯ
Е = Идет дождь, а у меня нет зонта	А = Идет дождь; В = У меня есть зонт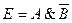
Е = Когда живется весело, то и работа спорится	А = Живется весело; В = Работа спорится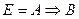
Е = Идет налево – песнь заводит, направо – сказку говорит	А = Идет налево; В = Идет направо; С = Песнь заводит; D = Сказку говорит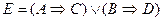

В формальной логике принято, что всякое простое высказывание обязательно имеет одно из двух значений – истина или ложь. Следует отметить, что значение не всегда известно. Примерами таких высказываний являются недоказанные или неопровергнутые гипотезы: предположение о существовании жизни на Марсе и т.п. Однако в случае простого высказывания всегда допустимо договориться о том, считать его истинным или ложным.

Сложное высказывание также является истинным или ложным, но это значение вычисляется. Вычисление производится по форме сложного высказывания в соответствии с таблицами истинности входящих в него логических операций. Следовательно, для определения значения истинности сложного высказывания надо уметь определять форму и знать правила логических операций.

Реальную задачу получаем, как правило, в виде текста на естественном языке. И прежде чем приступить к ее решению, надо выделить простые высказывания, отношения (связи) между ними и перевести их на язык формул (формализовать условие задачи, определить форму сложного высказывания).

При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:

1) инверсия; 2) конъюнкция; 3) дизъюнкция; 4) импликация и эквивалентность.

Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.

ДАНА ФОРМУЛА:	ПОРЯДОК ВЫЧИСЛЕНИЙ:
	1)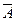	- инверсия;
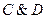
2)	- конъюнкция;
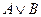
3)	- дизъюнкция;
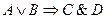
4)	- импликация;
5)	- эквивалентность.
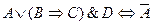
	1)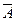	- инверсия;
2)	- импликация в скобках;
3)	- конъюнкция;
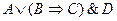
4)	- дизъюнкция;
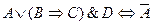
5)	- эквивалентность.

Значение сложного высказывания определяется по таблице истинности. Рассмотрим примеры определения значений сложных высказываний.

Дата добавления: 2014-01-11