ЭДС индукции

Рассмотрим, также как и при выводе выражения для работы перемещения контура, плоский контур, содержащий источник ЭДС, одна сторона у которого подвижна (см. рис. 2).

Источник с ЭДС равной 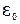создает в контуре ток , развивая при этом мощность, равную 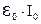. Эта мощность переходит в тепло, согласно закону Джоуля-Ленца ‑ . На основании закона сохранения энергии запишем:

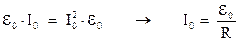
Возбудим теперь однородное магнитное поле, направленное от нас за чертеж. Вектор 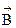совпадает с положительной нормалью к контуру , поэтому магнитный поток положителен. Согласно закону Ампера, каждый элемент контура будет испытывать силу со стороны магнитного поля. Подвижная сторона контура будет испытывать результирующую силу . Позволим теперь подвижной стороне перемещаться под действием этой силы вправо с постоянной скоростью .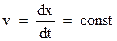

При этом, поскольку существует явление электромагнитной индукции (ведь у нас меняется магнитный поток через замкнутый контур), ток в контуре изменится, и станет 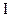. Соответственно изменится и результирующая сила, действующая на подвижную сторону. Она станет .

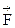Эта сила 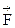за время совершит работу , равную:

Но согласно закону Ампера, эта сила равна:

Следовательно, выражение для работы примет вид:

т.е. ранее полученный результат.

Как и в случае неподвижных элементов контура, источником работы является источник тока, источник ЭДС.

В случае неподвижных элементов контура, вся работа, совершаемая источником ЭДС, превращается в тепло.

В случае движущейся стороны, ленц-джоулево тепло будет также выделяться, но другое, поскольку 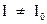. И, кроме того, будет совершена еще и механическая работа , выражение для которой мы определили выше.

Согласно закону сохранения энергии, теперь мы должны записать:

Отсюда получим:

Сравнивая получившееся выражение с законом Ома для полной цепи ‑ , приходим к выводу, что результирующая ЭДС, действующая в контуре, равна:

Таким образом, мы получаем, что ЭДС индукции равна:

(1)

где знак «‑» отражает правило Ленца.

Электронный механизм возникновения ЭДС индукции

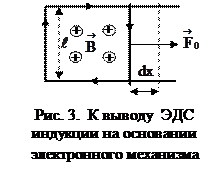Опять рассмотрим вышеприведенный контур, изображенный на рис. 3. Но теперь будем полагать, что источника 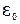нет. Т.е. существует контур с подвижной стороной в магнитном поле (см. рис. 3).

В отличие от предыдущего случая, будем перемещать подвижную сторону с некоторой скоростью . При этом на заряды внутри подвижной стороны (ведь это проводник и в нем существуют подвижные заряды), будет действовать сила Лоренца, направленная вдоль проводника:

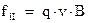
Сравнивая это выражение с выражением для силы, действующей на заряд, помещенный в электрическое поле напряженностью 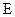‑ 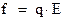, приходим к выводу, что действие этой силы Лоренца эквивалентно действию электрического поля с напряженностью

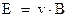
Это поле не электростатического происхождения, поэтому его циркуляция по замкнутому контуру отлична от нуля и даст величину ЭДС индукции:

Т.е., с точностью до знака получили тот же самый результат.

Остановимся на некоторых моментах.

1. Выше мы говорили, что действие силы Лоренца эквивалентно действию электрического поля.

Это не просто поверхностная аналогия. Это заключение имеет глубокий физический смысл.

В самом деле, перейдем в систему отсчета, связанную с движущимся проводником. Тогда мы скажем, что силы Лоренца нет, поскольку заряды в этой системе отсчета покоятся. Но в то же время существует электрическое поле, под действием которого заряды движутся.

При этом мы должны будем признать, что это электрическое поле обусловлено движущимся магнитным полем (ведь в этой системе отсчета магнитное поле движется).

Таким образом, уже сейчас мы приходим к выводу, что изменяющееся магнитное поле порождает электрическое поле. Т.е приходим к представлению о взаимосвязи поле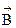й и и о их неразрывном единстве.

2. Ранее мы подчеркивали и говорили о том, что сила Лоренца работы не производит.

В то же время здесь мы считаем ЭДС индукции, которая является мерой работы, исходя из выражения для силы Лоренца. В чем же дело?

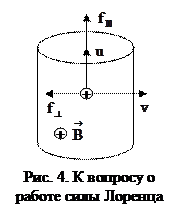Дело в том, что в расчетах мы брали не всю силу Лоренца, а только продольную (вдоль движущейся стороны) составляющую силы: 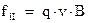. В действительности, поскольку заряды движутся вдоль проводника со скоростью упорядоченного движения (электрический ток), существует еще поперечная составляющая силы Лоренца (которая не сказывается на ЭДС, см. рис. 4). Следовательно, полная сила Лоренца будет равна:

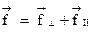
Выражение для работы этой силы можно представить как:

Второе слагаемое взято со знаком минус, поскольку сила направлена против скорости, против перемещения. Подставив выражения для сил 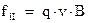и в выражение для работы , получим:

Т.е. действительно, работа полной силы Лоренца равна нулю, что и следовало ожидать.

3. Работа в контуре совершается за счет работы внешних сил, которые перемещают подвижную сторону. Т.к. подвижная сторона перемещается с постоянной скоростью, то ее ускорение равно нулю, и сумма всех приложенных к стороне сил равна нулю. Следовательно, выражение для внешних сил будет иметь вид:

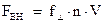
где ‑ сила, действующая на отдельную заряженную частицу (см. рис. 3.27), 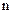‑ концентрация частиц ‑ число частиц в единице объема проводника, 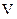‑ объем подвижной стороны.

Эта работа, согласно закону сохранения энергии, должна идти на выделение ленц-джоулева тепла. Действительно:

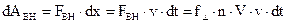
Подставим выражение для :

Здесь объем подвижной стороны мы представили как: . Но тогда произведение даст величину силы тока , так как плотность тока . Таким образом, выражение для работы внешних сил преобразуется к виду:

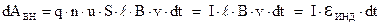
Где согласно выше показанному .

Таким образом, мы получили, что работа внешних сил равна работе ЭДС индукции.

Дата добавления: 2014-01-11