Взаимная индукция

Итак, в замкнутом контуре возникает ЭДС индукции , определяемая по закону:

Т.е. ЭДС индукции может возникать либо за счет изменения площади контура , либо за счет изменения индукции магнитного поля .

Поскольку магнитное поле может возбуждаться токами, текущими в каких либо проводниках, изменение индукции магнитного поля можно получить за счет изменения токов. Причем эти токи могут течь как в других контурах, так и в самом рассматриваемом контуре.

Если изменение индукции магнитного поля, соответственно и изменение магнитного потока, создается другим, по отношению к исследуемому, контуром, то говорят о взаимной индуктивности контуров, которую характеризуют коэффициентом взаимной индуктивности .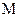

Если же изменение индукции магнитного поля создается током, текущим в самом исследуемом контуре, то говорят о самоиндукции контура, которую характеризуют коэффициентом самоиндукции .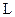

Вначале мы рассмотрим явление взаимоиндукции контуров, проводников.

Итак, имеются два, находящиеся недалеко друг от друга контура (см. рис. 5).

В цепь контура включен источник тока , который включается ключом 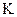. Сила тока в контуре изменяется с помощью реостата 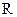. При этом в контуре течет ток 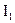. Этот контур , по которому течет ток 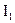, создает вокруг себя магнитное поле с индукцией .

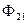В месте нахождения -го контура, магнитный поток, создаваемый -м контуром равен . Поскольку индукция поля прямо пропорциональна току 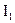, текущему в первом контуре, то и магнитный поток 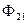будет прямо пропорционален току 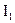‑ 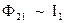. Чтобы записать знак равенства, введем коэффициент пропорциональности, который обозначим как :

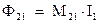
Здесь ‑ коэффициент взаимной индуктивности или взаимная индуктивность контуров и .

Взаимная индуктивность (коэффициент взаимной индуктивности) численно равен потоку магнитной индукции, создаваемому во втором контуре, если ток в первом контуре равен единице.

Размерность коэффициента взаимной индукции:

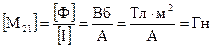
В СИ единица индуктивности имеет специальное наименование ‑ генри ‑ . Как мы выяснили ранее, размерность единицы индукции магнитного поля равна . Следовательно, размерность индуктивности будет иметь вид: . Это другой вид размерности индуктивности. Отсюда вытекает, что 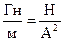. При изучении закона Ампера, мы установили, что магнитная постоянная имеет размерность . Сравнивая два последних выражения, мы приходим к выводу, что размерность магнитной постоянной можно представить в виде: . Это более употребительная форма размерности магнитной постоянной, так как в таком виде она симметрична размерности электрической постоянной .

Далее, возвращаясь к взаимодействующим посредством магнитного поля контурам, можно рассуждать и наоборот. Во втором контуре имеется источник тока, второй контур создает магнитное поле и т.д. В результате мы придем к аналогичной формуле:

Из соображений симметрии ясно, но это можно и показать, что для одних и тех же двух контуров коэффициенты взаимной индуктивност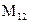и и равны друг другу. Т.е. в действительности есть лишь взаимная индуктивность контуров:

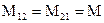
И для магнитного потока, создаваемого током 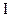, можно записать общее выражение:

(2)

Т.о., во втором контуре возникает ЭДС индукции, равная:

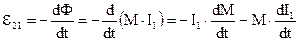
Если контуры неподвижны друг относительно друга и если не меняется их конфигурация, то:

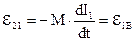
Здесь необходимо отметить еще следующее обстоятельство. Очевидно, что коэффициент взаимной индуктивности 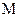зависит от магнитных свойств среды, вмещающей контура. А магнитные свойства среды в общем случае зависят от магнитного поля, существующего в среде (например, ферромагнетики). Т.е., в конечном счете, от тока 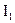, т.е. от времени. Следовательно, в этом случае (ферромагнетики) 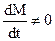, даже, если площадь контуров постоянна.

Исходя из последней формулы, можно дать другое определение коэффициенту взаимной индуктивности.

Коэффициент взаимной индуктивности двух контуров численно равен ЭДС индукции, возникающей в одном из контуров, при изменении силы тока в другом на единицу за единицу времени.

Для многосвязанных контуров магнитный поток увеличивается в 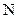раз, где 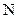‑ число витков многосвязанных контуров. При этом вместо потока 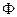рассматривают величину ‑ потокосцепление, равную:

Коэффициент взаимной индукции двух контуров

Найдем коэффициент взаимной индукции двух катушек, намотанных на общий тороидальный сердечник.

Мы уже показывали, что индукция магнитного поля тороида (6), приближенно может быть определена по формуле для магнитного поля соленоида:

Здесь 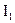‑ ток, текущий через первую катушку, ‑ число витков на единицу длины первой катушки. Если магнитная проницаемость сердечника 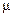(об этой физической величине мы поговорим более подробно несколько позже), то индукция магнитного поля в сердечнике будет равна:

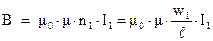
Здесь 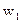‑ число витков первой катушки, 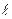‑ длина тороида по средней линии. В этом случае, магнитный поток в сердечнике будет равен:

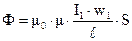
где ‑ площадь поперечного сечения сердечника тороида.

Поток магнитосцепления , пронизывающий вторую катушку, будет равен:

В этом случае, по определению:

(3)

Дата добавления: 2014-01-11