Разложение правильной дробно-рациональной функции на простейшие дроби

◙ Функция вида 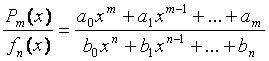называется дробно-рациональной функцией ( или рациональной дробью).

При этом если m < n, то рациональная дробь правильная; если m > n – рациональная дробь неправильная. Неправильную дробь всегда можно представить в виде: ,

где M (x) – многочлен, – правильная дробь.

Среди правильных дробей различают четыре типа простейших дробей:

, , , ,

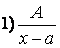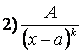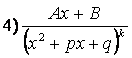где 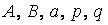– действительные числа, 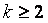– натуральное число, квадратный трёхчлен 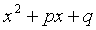не имеет действительных корней.

З а м е ч а н и е. Любую правильную дробь 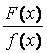можно разложить в сумму простейших дробей. При этом вид разложения определяется корнями знаменателя f (x).

1 случай. Корни знаменателя действительны и различны, т.е.

,

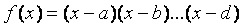тогда ,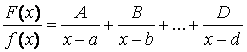

где A, B, …, D – неопределенные коэффициенты.

2 случай. Корни знаменателя действительны, причем некоторые из них кратные: ,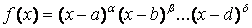

тогда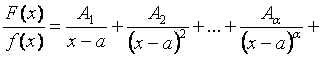

, (*)

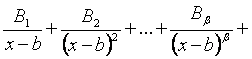
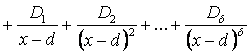где A_i, B_i, …, D_i – неопределенные коэффициенты.

3 случай. Среди корней знаменателя есть комплексные различные:

,

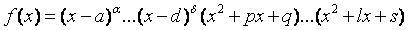тогда ,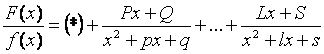

где Р, Q, …, S – неопределенные коэффициенты.

4 случай. Среди корней знаменателя есть комплексные кратные:

,

тогда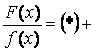

,

где P_i, Q_i, …, S_i – неопределенные коэффициенты.

З а м е ч а н и е. Неопределённые коэффициенты вычисляются следующим образом: приводим к общему знаменателю сумму дробей в правой части равенства и приравниваем числители. Далее составляем систему линейных уравнений относительно искомых коэффициентов одним из двух способов:

1 способ: приравнивая коэффициенты при одинаковых степенях х в левой и правой частях последнего тождества;

2 способ: придавая переменной х в этом тождестве произвольные числовые значения.

Дата добавления: 2014-01-11