Интегральные суммы

Пусть y = f (x) – непрерывная функция на [ a, b ];

т, М – наименьшее и наибольшее значения функции на [ a, b ].

Разобьем [ a, b ] на п частей: a = х ₀ < х ₁ < х ₂ < …< х_п = b.

Положим х₁ – х₀ = D х₁, х₂ – х₁ = D х₂, …, х_п – х_п-1 = D х_п .

Обозначим наибольшее и наименьшее значения f (x) на [ х ₀, х ₁] через т ₁ и М ₁, на [ х ₁, х ₂] через т ₂ и М ₂,…, на [ х_{п -1}, х_п ] через т_п и М_п.

Составим интегральные суммы:

1) нижняя интегральная сумма 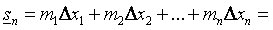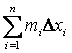; 2) верхняя интегральная сумма ;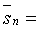

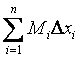Свойства верхней и нижней интегральных сумм:

а) ;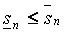

б) ;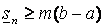

в) ;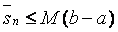

г) .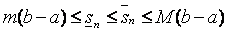

Определенный интеграл

Возьмем точки x ₁, x ₂, …, x_п: х ₀ < x ₁ < х ₁, х ₁ < x ₂ < х ₂ , …, х_{п- 1} < x_п < х_п.

Каждой точке x_i сопоставим значение f (x_i), .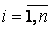

Составим интегральную сумму для f (x) на [ a, b ]:

.

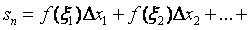
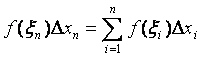Т.к. m_i £ f (x_i) £ M_i " x_i Î [ x_{i -1}, x_i ] (),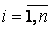

то m_i D x_i £ f (x_i)D x_i £ M_i D x_i, следовательно, .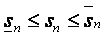

Пусть max D x_i – наибольшая из длин отрезков [ x ₀ , x ₁], [ x ₁ , x ₂], …, [ x_{п- 1} , x_п ].

Заметим, что если max D x _i ® 0, то п ® ¥.

◙ Если при любых разбиениях отрезка [ a, b ] таких, что max D x_i ® 0, и при любом выборе точек x_i на отрезках [ x_{i- 1}, x_i ] интегральная сумма

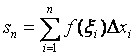стремится к одному и тому же пределу s, то этот предел называют определен-

ным интегралом от функции f (x) на отрезке [ a, b ]и обозначают .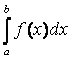

Таким образом, по определению, 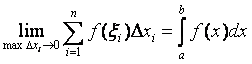, где

a – нижний предел интеграла, b – верхний предел интеграла,

[ a, b ]– отрезок интегрирования, х – переменная интегрирования.

◙ Если для функции f (x) выше указанный предел существует, то функцию называют интегрируемой на отрезке [ a, b ].

З а м е ч а н и е. Т.к. 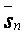,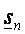– частные случаи интегральной суммы s_п, то 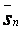, 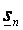® s, поэтому

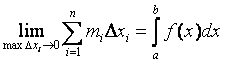и .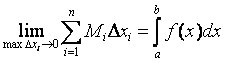

Геометрический смысл определенного интеграла (в случае f (x) ³ 0):

определенный интеграл 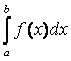численно равен площади криволинейной трапеции, ограниченной кривой y = f (x), прямыми x = a, x = b и осью Ох.

Основные свойства определенного интеграла:

1) ;

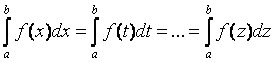2) ;

3) ;

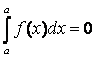4) 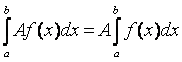, А = const;

5) ;

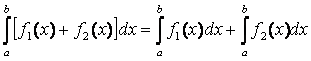6) 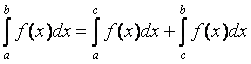" a, b, c Î R,

если только все эти три интеграла существуют;

7) если f (x) £ j (x) на отрезке [ a, b ] (a < b), то ;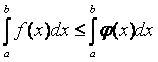

8) если т и М – наименьшее и наибольшее значения функции f (x) на [ a, b ]

и a £ b, то 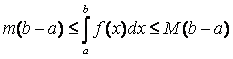; (Рисунок 2.3.1)

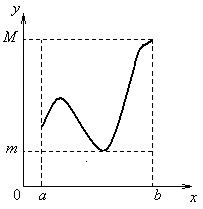
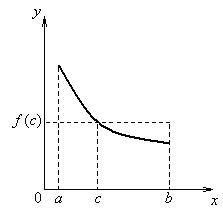
Рисунок 2.3.1 Рисунок 2.3.2

9) (Теорема о среднем) Если f (x) непрерывная функция на [ a, b ], то $ с Î[ a, b ]:

.

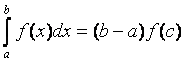При этом f (с) называется средним значением функции на отрезке [ a, b ]. (Рисунок 2.3.2)

10)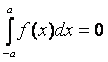, если 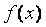– нечётная функция;

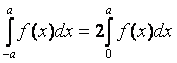, если 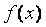– чётная функция.

Вычисление определенного интеграла

Дата добавления: 2014-01-11