
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Галкин С.В
|
|
|
|
Приложения
Приложение 1. Виды пределов и методы их вычисления
Т а б л и ц а 4.1
| Виды пределов | Результат подстановки предельной точки | Результат или метод вычисления предела |
1. 
|  неопределённость
неопределённость
| 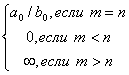
|
2.
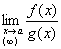
|  , ,  неопределённости неопределённости
| а) разложение на множители; б) правило Лопиталя; в) умножение на сопряжённое выражение; г) применение эквивалентных бесконечно малых; д) правило 1 этой таблицы |
3. 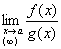
| 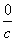 , , 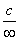 , , 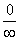
| |
4. 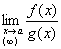
| 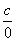 , , 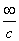 , , 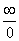
| 
|
5. 
|  неопределённость
неопределённость
| привести к неопределённостям вида  или или  , затем как в 1 или 2 этой таблицы , затем как в 1 или 2 этой таблицы
|
6. 
|  , , 
| 
|
7. 
|  , , 
| |
8. 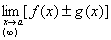
|  неопределённость неопределённость
| привести к неопределённостям вида  или или  , затем как в 1 или 2 этой таблицы , затем как в 1 или 2 этой таблицы
|
9. 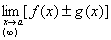
| 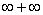
| 
|
10. 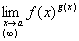
|  неопределённости неопределённости
| а) привести ко второму замечательному пределу  ;
б) использовать формулу ;
б) использовать формулу 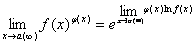
|
11. 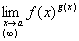
| 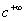
| 
|
12. 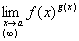
| 
| 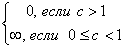
|
Приложение 2. Таблица эквивалентных бесконечно малых
Т а б л и ц а 4.2
 , т.е. , т.е.  – бесконечно малая при – бесконечно малая при 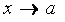 , а £ ¥. , а £ ¥.
| ||
1. 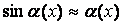
| 5. 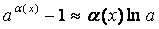
| 9.
|
2. 
| 6. 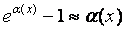
| 10.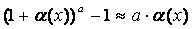
|
3. 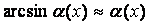
| 7. 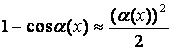
| 11. 
|
4. 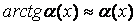
| 8. 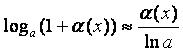
|
Приложение 3. Производные основных элементарных функций.
Т а б л и ц а 4.3
1. 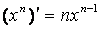
| 7. 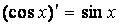
| 13. 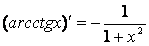
|
2. 
| 8. 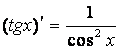
| 14. 
|
3. 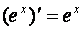
| 9. 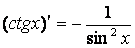
| 15. 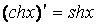
|
4. 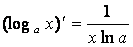
| 10. 
| 16. 
|
5. 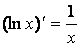
| 11. 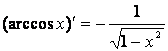
| 17. 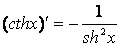
|
6. 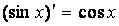
| 12. 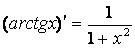
|
Список литературы
1. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. – М.: Наука, 1973. – 720 с.
2. Бугров Я.С., Никольский С.М. Вывшая математика. Дифференциальное и интегральное исчисления. – М.: Наука, 1980. – 432 с.
3. Натансон И.П. Краткий курс высшей математики. – СПб.: Издательство Лань, 1997. – 736 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.1–456 с.
5. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учебник для втузов: В 2 т.–М.: Наука, 1976.–Т.2–576 с.
6. Хасеинов К.А. Каноны математики. Учебник. – Алматы: 2003. – 686 с.
Содержание
Предисловие 3
1 Введение в анализ
Дифференциальное исчисление функции одной переменной
1.1 Лекция 1. Функция. Числовая последовательность. Пределы 4
1.2 Лекция 2. Непрерывность функций 8
1.3 Лекция 3. Дифференциальное исчисление функции одной переменной 12
1.4 Лекция 4. Исследование функций с помощью производных 16
2 Функции нескольких переменных
Интегральное исчисление функции одной и нескольких переменных 20
2.1 Лекция 5. Первообразная и неопределенный интеграл 20
2.2 Лекция 6. Интегрирование рациональных, иррациональных,
тригонометрических функций 23
2.3 Лекция 7. Определённый интеграл, основные свойства.
Формула Ньютона-Лейбница. Методы подстановки.
Интегрирование по частям 28
2.4 Лекция 8. Двойные интегралы 32
2.5 Лекция 9. Тройные интегралы 36
3 Дифференциальные уравнения. Ряды 40
3.1 Лекция 10. Дифференциальные уравнения, основные понятия 40
3.2 Лекция 11. Линейные дифференциальные уравнения высших
порядков. Линейные однородные и неоднородные
дифференциальные уравнения высших порядков
с постоянными коэффициентами 45
3.3 Лекция 12. Числовые ряды. Функциональные ряды.
Степенные ряды, ряды Тейлора 50
4 Приложения 57
Список литературы 59
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 339; Нарушение авторских прав?; Мы поможем в написании вашей работы!