
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Корпускулярно-волновые свойства частиц
|
|
|
|
Если электрон движется со скоростью  , то его импульс равен
, то его импульс равен  . Следовательно, движущемуся электрону соответствует длина волны
. Следовательно, движущемуся электрону соответствует длина волны 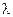 , равная:
, равная:

При прохождении электроном разности потенциалов 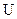 электрон приобретает скорость
электрон приобретает скорость  , равную:
, равную:

В этом случае, длина волны, соответствующая электрону, будет равна:
 (2)
(2)
Подставляя численные значения констант, получим:

Напряжении в электронно-лучевой трубке меняется в пределах от  до
до  . Следовательно, длина волны электрона лежит в пределах от
. Следовательно, длина волны электрона лежит в пределах от  до
до  , т.е. в диапазоне рентгеновского излучения. Следовательно, появляется реальная возможность проверки гипотезы Луи-де-Бройля, проверив, дифрагируют ли электронные пучки на кристаллах.
, т.е. в диапазоне рентгеновского излучения. Следовательно, появляется реальная возможность проверки гипотезы Луи-де-Бройля, проверив, дифрагируют ли электронные пучки на кристаллах.
В 1927 г. Девисон и Джермер исследовали явление рассеяния электронов на кристалле никеля. Никель был ранее изучен с помощью рентгеновских лучей, и поэтому постоянная его решетки была хорошо известна.
Если электрон обладает волновыми свойствами, то при рассеянии на кристалле должны быть направления максимумов и направления минимумов. И это действительно подтвердилось в эксперименте. Причем экспериментально измеренная длина волны электрона в точности соответствовала теоретической.
Советский ученый Тартаковский исследовал явление прохождения электронного пучка через тонкие металлические фольги. При этом получалась дифракционная картина в точности такая же, как и при прохождении рентгеновских лучей.
Этими, и подобными им экспериментами было доказано, что электрон действительно обладает волновыми свойствами.
Причем было показано, что волновые свойства присущи каждому электрону в отдельности, а не большой совокупности электронов в целом.
Таким образом, накапливались данные о корпускулярно-волновом дуализме электрона.
Эксперименты, указывающие на волновую природу электрона.
1. Дифракция электронов, следовательно ‑ электрон не шарик, а сложное образование, структура, обладающая волновыми свойствами.
2. В зависимости от внешних условий структура электрона меняется, т.е. структура электрона зависит от его взаимодействия с окружающей средой.
3. Область локализации электрона в атоме ‑ электронная оболочка. В то же время при прохождении через кристалл, электрон взаимодействует одновременно со множеством атомов, о чем свидетельствует острота дифракционных максимумов. Т.е. здесь область локализации электрона совершенно другая.
Корпускулярная природа электрона.
Электрон действует всегда как единое целое, не дробясь на части. Однако его неделимость не обусловлена его точечностью, а имеет гораздо более сложную природу, разгадка которой дело будущего.
Волновые свойства электронов позволяют их использовать в так называемом электронно-структурном анализе, который дает лучшие результаты, в отличие от рентгеноструктурного анализа.
Это происходит потому, что рентгеновские фотоны взаимодействуют только с электронной оболочкой атома, а электроны взаимодействуют в основном с ядром атома.
Как видно из формулы (3.11), длина волны частицы, при прочих равных условиях, обратно пропорциональна корню квадратному из массы частицы.
Таким образом, если для электрона энергии  длина волны получается равной
длина волны получается равной  , то для протона, той же энергии, длина волны будет равна:
, то для протона, той же энергии, длина волны будет равна:
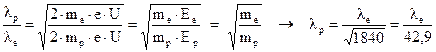
Отсюда получаем, что длина волны протона энергией  равна
равна

А для молекулы кислорода ‑  .
.
Причем здесь мы предположили, что гипотеза Луи-де-Бройля распространяется и на сложные, составные частицы. Это предположение было подтверждено экспериментально, путем получения дифракционной картины от атомов гелия.
Если мы возьмем пылинку, массой  , движущейся со скоростью
, движущейся со скоростью  , то для де-Бройлевской длины волны получим значение:
, то для де-Бройлевской длины волны получим значение:

Т.е. ничтожно малая длина волны.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 558; Нарушение авторских прав?; Мы поможем в написании вашей работы!