Включення в портфель безризикових цінних паперів

Нехай х – частка капіталу, що інвестор розмістив у вигляді портфеля Е (m_E; s_E), сформованого на основі ризикових вкладень, (1 – х) – частка засобів, розміщена під фіксований відсоток R_F у безризикові ЦП. Випадкова величина норми прибутку такого розміщення капіталу: R_П = (1 – x) R_F + xR_E; сподівана норма прибутку: m_П = (1 – x) R_F + xm_E; а оцінка ризику, враховуючи що 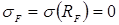, , 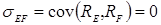дорівнює:

.

Отже, х = s_П /s_Е. Звідси можемо отримати рівняння залежності сподіваної норми прибутку від ступеня ризику: .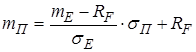

Це рівняння в просторі (m – s) визначає пряму, яка називається лінією ринку капіталів і характеризує ПЦП, що складаються як з безризикових ЦП, так і з ЦП, обтяжених ризиком (пряма R_FE на рис.2.1.9)

Випадок, коли 0 < x < 1 можна розглядати як ситуацію надання кредиту (інвестування) під фіксований відсоток R_F.

Випадок, коли х > 1 означає, що інвестор може скористатись позичкою та інвестувати у ринковий портфель Е (m_E; s_E) більше, ніж величина його власного початкового капіталу – ситуація отримання кредиту під фіксований відсоток R_F.

Ринкова модель (однофакторна модель Шарпа формування норми прибутку)

Норми прибутків більшості акцій тісно пов’язані з загальною доходністю ринку ЦП, яка змінюється під впливом макроекономічних, політичних та інших чинників. Цю залежність американський економіст В.Шарп відобразив у, так званій, ринковій моделі:

R_i = a_i + b_i R_М + e_i,

тут R_і – норма прибутку і -ої акції, a_i – коефіцієнт зміщення, b_i – коефіцієнт нахилу, R_М – норма прибутку ринкового портфеля, e_i – випадкове відхилення (випадкова величина, для якої ).

Ринковий портфель – це портфель, який включає всі наявні на ринку ЦП, в пропорції, що відповідає часткам окремих ЦП в загальній капіталізації ринку. Для моделювання в якості ринкового портфеля використовують певний фондовий індекс (наприклад, в США – Standard and Poor’s 500). При цьому виникає проблема адекватності подібної заміни – наскільки повно та точно індекс може характеризувати всі ЦП, присутні на ринку.

Коефіцієнт “ бета ” для i- ої акції обчислюється таким чином:

; .

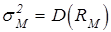Для акції, норма прибутку якої віддзеркалює прибутковість ринку, коефіцієнт b дорівнює 1. У свою чергу, акціям з коефіцієнтом b більшим за одиницю, властива більша мінливість норми прибутку, ніж ринку в цілому. Їх називають “ агресивними акціями ”. І навпаки, акції з коефіцієнтом b меншим за одиницю мають меншу мінливість, ніж ринок у цілому, і їх називають “ оборонними акціями ”.

Дата добавления: 2014-01-11