Операции над нечеткими множествами

1.Включение. Пусть A и B – нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если "x ÎE m_A(x) > m_B(x). Обозначение: A Ì B.

2. Равенство. A и B равны, если "xÎE m_A(x) = m_B(x). Обозначение: A = B.

3. Дополнение. Пусть M = [0, 1], A и B – нечеткие множества, заданные на E. A и B дополняют друг друга, если "xÎE m_A(x) = 1 – m_B(x). Обозначение: B = 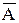или A = 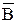. Очевидно, что .

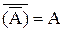4.Пересечение. A Ç B – наибольшее нечеткое подмножество, содержащееся одновременно в A и B;

m _{A Ç B} (x) = min{m_A(x), m_B(x)}.

5.Объединение. А È В – наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности

m _{AÈ B} (x) = max {(m_A(x), m_B(x)}.

6. Разность. А \ B= А Ç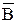с функцией принадлежности:

m_A\B(x) = min { m_A(x), 1 – m_B(x)}.

Например, пусть: A = 0,4/ x₁ È 0,2/ x₂ È 0/ x₃ È 1/ x₄;

B = 0,7/ x₁ È 0,9/ x₂ È 0,1/ x₃ È1/ x₄;
C = 0,1/ x₁ È 1/ x₂ È 0,2/ x₃ È 0,9/ x₄.

Здесь:

1. A Ì B, т.е. A содержится в B, С несравнимо ни с A, ни с B.

2. A ¹ B ¹ C.

3. 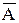= 0,6/ x₁ È 0,8/ x₂ È 1/ x₃ È 0/ x₄;
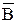= 0,3/ x₁ È 0,1/ x₂ È 0,9/ x₃ È 0/ x₄.

Для нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения m_A(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами.

Рис. 1. Рис. 2

Рис. 3. Рис. 4.

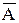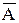На рис. 1 темная часть соответствует нечеткому множеству A. На Рис. 2 – 4 даны , A Ç , AÈ 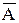, соответственно.

Свойства операций. Пусть А, В, С – нечеткие множества, тогда выполняются следующие соотношения:

а) 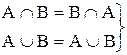– коммутативность;

б) 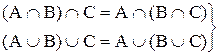– ассоциативность;

в) 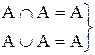– идемпотентность;

г) 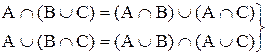– дистрибутивность;

д) AÈÆ = A, где Æ – пустое множество, т.е. m_Æ(x) = 0"xÎE;

AÇÆ = Æ;

AÇE = A, где E – универсальное множество;

AÈE = E;

е) 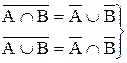– теоремы де Моргана.

В отличие от четких множеств, для нечетких множеств в общем случае AÇ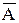≠ Æ, A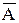ȹ E, что, в частности, проиллюстрировано выше в примере наглядного представления нечетких множеств.

Тема 4. Бинарные отношения

Дата добавления: 2014-01-11