Описание и организация выбора

Задача выбора возникает, когда из некоторого конечного или бесконечного множества надо отобрать подмножество в каком-то смысле хороших элементов.

Пусть Х – исходное множество альтернатив. Подмножество отбираемых элементов называется выбором, и обозначается С(Х) (от английского choice –выбор). Алгоритм, реализующий этот отбор, называется механизмом выбора.

Рассмотрим примеры наиболее распространенных механизмов выбора.

1) Скалярный оптимизирующий механизм – выбор вариантов, при которых некоторая скалярная функция f(х) достигает максимума

С_опт(Х) = { хÎХ | х = arg max f(x) }

2) Условно-оптимальный механизм – выбор по схеме математического программирования, т.е. выбор таких хÎХ, при которых достигается условный максимум скалярной функции f₀(x) при выполнении системы ограничений

С_мп(Х) = { хÎХ | х = arg max f₀(x) | f _i(х) £ 0, i = 1,.., m] }.

Перечисленные механизмы базируются, как нетрудно догадаться, на критериальном языке описания выбора. Следующие два механизма основаны на использовании языка бинарных отношений.

3) Механизм доминирования по бинарному отношению R – выбор тех хÎХ, которые с любым элементом из Х находится в отношении R (элемент х лучше любого y в смысле отношения предпочтении R)

С_R(Х) ={ хÎХ | " yÎХ: (x, y)ÎR }

4) Механизм блокировки по бинарному отношению R – выбор тех элементов xÎX, для которых в Х нет элемента лучше в смысле отношения предпочтения R

С^R(Х) = { хÎХ | " yÎХ: (y, х)ÏR }.

Приведем несколько теорем о свойствах выбора.

Теорема 4.1. Пусть имеем два отношения R1 и R2, такие, что R2 = (R1)^d. Тогда а) С_R1(Х) = С^R2(Х) и б) С^R1(Х) = С_R2(Х).

Доказательство. Пусть х Î С^R2(Х). По определению С^R2(Х) = { хÎХ | " yÎХ: (y, х)ÏR2 }. Пусть (y, х)ÏR2 = 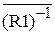. Это означает, что (у, х) Î(R1)^–1, или (х, у) ÎR1. Так как последнее соотношение выполняется для любого у ÎХ, то значит х Î С_R1(Х). Следовательно, С^R2(Х) Í С_R1(Х).

Обратное включение и свойство б) доказывается аналогично, т.к. для любого отношения R выполняется равенство .

На основании данной теоремы получаем, что свойства механизмов доминирования и блокировки во многом совпадают.

Приведем без доказательства также следующие теоремы о выборе.

Теорема 4.2. Бинарное отношение R порождает непустой выбор (т.е. содержащий хотя бы один элемент), основанный на механизме доминирования или блокировки тогда и только тогда, когда R ациклично.

Теорема 4.3. Бинарное отношение R порождает однозначный выбор (т.е. содержащий ровно один элемент), основанный на механизме доминирования или блокировки тогда и только тогда, когда R ациклично и слабо полно.

Задание. Указать такое бинарное отношение, при котором механизм доминирования совпадает со скалярно-оптимизирующим механизмом выбора.

Дата добавления: 2014-01-11