Качественный порядок

Дополним отношение строгого упорядочения P_уп свойством транзитивности. Назовем полученное отношение качественным порядком P_кач. Рассмотрим два примера такого отношения.

1) Пусть х, у – вещественные числа. Введем качественный порядок следующим соотношением:

хР_качу Û x > у + 1.

Очевидно, что в данном случае отношение Р_кач асимметрично и транзитивно, но оно не является негатранзитивным. Покажем это.

Дополнение к введенному отношению определим как

х`Р_кач у <=> х £ у + 1

Положим у = 0; х = 0.9; z = – 0.9. Тогда, очевидно, выполняются отношения (х, y) Î`Р<sub>кач</sub>; (y, z) Î`Р_кач; (х, z) Ï Р_кач. Т.е. условие негатранзитивности не выполняется.

Согласно рассмотренному примеру, а также доказанному ранее свойству транзитивности слабого порядка, можно сделать вывод, что асимметричное негатранзитивное отношение является транзитивным, но обратное не всегда верно.

2) Введем на множестве точек n-мерного евклидова пространства следующее отношение Par, называемое отношением Парето:

х, уÎРаr Û " i: х_i ³ y_i и $ j: х_j > у_j.

Отношение Парето называется также безусловным критерием предпочтения (БКП). Оно означает, что точка x по всем координатам имеет не меньшие значения, чем точка y и хотя бы по одной координате имеется строгое превосходство. В двумерном случае данное отношение можно изобразить графически. Возможны следующие ситуации:

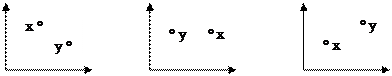а) x₁ < y₁ б) x₁ > y₁ в) x₁ < y₁

x₂ > y₂ x₂ = y₂ x₂ < y₂

нет отношения Раr; есть отношение Раr, есть отношение Раr,

x лучше y; y лучше x.

Задание. Доказать, что отношение Раr является качественным порядком.

Дата добавления: 2014-01-11