Косвенный метод наименьших квадратов (КМНК)

Как уже отмечалось, КМНК применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.

1. Структурная модель преобразовывается в приведенную форму модели.

2.Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты (δ).

3.Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.

Рассмотрим применение КМНК для простейшей идентифицируемой эконометрической модели с двумя эндогенными и двумя экзогенными переменными:

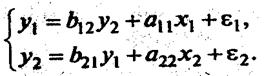
Пусть для построения данной модели мы располагаем некоторой информацией по пяти регионам:

Регион	У1	У2	Х1	Х2
Средние		6,2	2,4	3,4

Приведенная форма модели составит:

где и₁, и₂ — случайные ошибки приведенной формы модели.

Для каждого уравнения приведенной формы модели применяем традиционный МНК и определяем δ-коэффициенты.

Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т. е. Y = у - Yср и X = х — Xср. Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:

Применительно к рассматриваемому примеру, используя отклонения от средних уровней, имеем:

Решая данную систему, получим следующее первое уравнение приведенной формы модели:

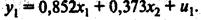
y1=0,685+0,852*x1+0,373*x2

Аналогично применяем МНК для второго уравнения приведенной формы модели, получим:

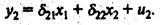
Система нормальных уравнений составит:

.

Применительно к нашему примеру имеем:

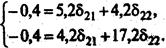
Откуда второе приведенное уравнение составит:

y2=6,39-0,072*x1-0,006*x2

Таким образом, приведенная форма модели имеет вид:

Переходим от приведенной формы модели к структурной форме модели, т. е. к системе уравнений:

Для этой цели из первого уравнения приведенной формы модели надо исключить х₂, выразив его из второго уравнения приве­денной формы и подставив в первое:

Тогда

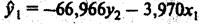-первое уравнение структурной модели.

Чтобы найти второе уравнение структурной модели, обратимся вновь к приведенной форме модели. Для этой цели из второго уравнения приведенной формы модели следует исключить х_2, выразив его через первое уравнение и подставив во второе:

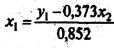
и

— второе уравнение структурной формы модели.

Итак, структурная форма модели имеет вид:

.

Δy1=-66,966Δy2-3.97Δx1+ε1

Δy2=-0.085Δy1+0.26Δx2+ ε2

Эту же систему можно записать, включив в нее свободный член уравнения, т. е. перейти от переменных в виде отклонений от среднего уровня к исходным переменным у и х.

Свободные члены уравнений определим по формулам:

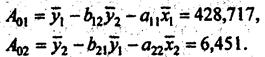
Тогда структурная модель имеет вид:

Оценка значимости модели дается через F -критерий и R^2 для каждого уравнения в отдельности. В рассматриваемом примере хороших результатов достичь не удалось: ввиду малого числа на­блюдений значения F-критерия Фишера несущественны (при уровне значимости 0,05 F -табличное значение равно 19, а факти­ческое F= 7 для первого уравнения).

Если к каждому уравнению структурной формы модели при­менить традиционный МНК, то результаты будут резко отличаться:

Как видим, не совпадают даже знаки коэффициентов при Пе­ременных: в первом уравнении структурной формы коэффици­енты меньше нуля, а в уравнении регрессии больше нуля; во вто­ром уравнении обратное воздействие у_х нау₂ в структурной моде­ли сменяется на прямое в уравнении регрессии, а с фактором х₂ наоборот.

Различия между коэффициентами регрессии и структурными коэффициентами модели численно могут быть и менее сущест­венными. Так, например, Г.Тинтнер, рассматривая статическую модель Кейнса для австрийской экономики за 1948-1956 гг., получил функцию потребления классическим МНК в виде

С = 0,782у + 71,6, а используя КМНК,

С = 0,781у + 73,212¹.

При сравнений результатов, полученных традиционным МНК и с помощью КМНК, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов. Как показал Т. Хаавельмо, рассматривая две взаимосвязанные регрессии:

коэффициент регрессии отличается от структурного коэффици­ента и совпадает с ним только в одном частном случае, когда переменная у не содержит ошибок (т. е. ε = 0), а ошибки переменной х имеют дисперсию, равную единице.

Кроме того, при интерпретации коэффициентов множественной регрессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии Y^1=-1,09+0,364у₂+1,192X1 показывает, что с ростом X1 на единицу Y1 возрастает в среднем на 1,192 ед. при неизменном уровне значения у₂. Между тем в соответствии с системой одновременных уравнений переменная у₂ не может быть неизменной, ибо она в свою очередь зависит от у1.

Нарушение предпосылки независимости факторов друг от друга при использовании традиционного МНК в системе одновременных уравнений приводит к несостоятельности оценок структурных коэффициентов. В ряде случаев они оказываются экономически бессмысленными. Опасность получения таких результатов возрастает при увеличении числа эндогенных переменных в правой части системы, ибо становится невозможным расщепить совместное влияние эндогенных переменных и видеть изолированные меры их воздействия в соответствии с предпосылками традиционного МНК.

Дата добавления: 2014-01-11