
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Двухшаговый метод наименьших квадратов (ДМНК)
|
|
|
|
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).
Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.
Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной У^i = δi1 х1 + δi2 х2 +... + δij хj и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
•все уравнения системы сверхидентифицируемы;
•система содержит наряду со сверхидентифицируемыми точно сли все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Применим ДМНК к простейшей сверхидентифицируемой модели:

Данная модель может быть получена из предыдущей идентифицируемой модели:

если наложить ограничения на ее параметры, а именно:
b12=a11
В результате первое уравнение стало сверхидентифицируе-мым: H= 1 (у1), D = 1 (х2) и D + 1 > Н. Второе уравнение не изменилось и является точно идентифицируемым: H = 2 и D = 1, D + 1 = H.
На первом шаге найдем приведенную форму модели, а именно:
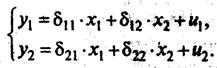 .
.
Предполагая использование тех же исходных данных, что и в предыдущем примере, получим ту же систему приведенных уравнений:
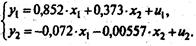
На основе второго уравнения данной системы можно найти теоретические значения для эндогенной переменной у2, т. е. у2. С этой целью в уравнение

 у2 = - 0,072 x1 - 0,00557 х2 + и2
у2 = - 0,072 x1 - 0,00557 х2 + и2
подставляем значения х, и х2 (в нашем примере это отклонения от средних уровней). Оценки для эндогенной переменной у2 приведены в табл. 4.1 (гр. 3).
Таблица 4.1 Расчетные данные для второго шага ДМНК
| X1 | x2 |  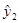
| 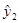 +x1=z +x1=z
| Y1 | Y1z | 
|
| -1,4 | -0,4 | 6,103 | -1,297 | -2 | 2,594 | 1,682 |
| -0,4 | -2,4 | 0,042 | -0,358 | -1 | 0,358 | 0,128 |
| 0,6 | -1,4 | -0,035 | 0,565 | 0,319 | ||
| -0,4 | 1,6 | 0,020 | -0,380 | -0,380 | 0,144 | |
| 1,6 | 2,6 | -0,130 | 1,470 | 2,940 | 2,161 | |
| Сумма | 5,512 | 4,434 |
После того как найдены оценки эндогенной переменной у2, обратимся к сверхидентифицируемому структурному уравнению
У1^=b12(y2+x1)
Заменяя фактические значения у2 их оценками у2, найдем значения новой переменной
 +x1=z
+x1=z
Далее применяем МНК к уравнению
У1 =b12*z,
т. е.

Откуда
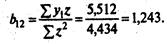
Таким образом, сверхидентифицируемое структурное уравнение составит:
У1 = 1,243 •(y2 + x1).
Ввиду того, что второе уравнение нашей системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений, та же:
 у2 = -0,085 •y1 + 0,026 • х2.
у2 = -0,085 •y1 + 0,026 • х2.
В целом рассматриваемая система одновременных составит:
ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений Для точно идентифицируемых уравнений ДМНК. Дает тот же результат, что и КМНК. Поэтому в ряде компьютерных программ, например DSTAT, для решения системы одновременных уравнений рассматривается лишь ДМНК.
Решение сверхидентифицируемой модели на компьютере построено на предположении, что при каждой переменной в правой части системы имеется свой структурный коэффициент. Если же в модель вводятся ограничения на параметры, как в рассмотренном примере b12 = a11, то программа DSTAT не работает. Структурная модель может принимать любой вид, но без ограничений на параметры При этом должно выполнятся счетное правило идентификации. D+l>H. Так, если структурная модель имеет вид:

где первое уравнение сверхидентифииируемо, а второе - точно идентифицируемо, то реализация модели в ППП DSTAT оказывается следующей.
Последовательно ДМНК применяется к каждому уравнению Эндогенная переменная, находящаяся в левой части системы" рассматривается как зависимая переменная, а переменные содержащиеся в правой части системы (эндогенные и экзогенные) - как факторы, которые должны быть пронумерованы. Так при вводе информации о переменных в последовательности У[ у2 x, х2, х3 для первого уравнения имеем: у2 — фактор 2; х, - фактор 3.
Далее отвечаем на следующие вопросы программы DSTAT.
Эндогенная переменная — это фактор №? Ответ: 2.
Экзогенная переменная, входящая в уравнение,- это фактор №? Ответ: 3.
Не входящая в уравнение экзогенная переменная — это фактор №? Ответ: 4.
Не входящая в уравнение экзогенная переменная — это фактор №? Ответ: 5.
По окончании процедуры выдается уравнение

и приводится оценка его качества через F-критерий Фишера, относительную ошибку аппроксимации и оценки значимости структурных коэффициентов модели через t -критерий Стьюдента.
Аналогично поступаем со вторым уравнением системы. В нем соответственно эндогенная переменная ух рассматривается как фактор 1, а экзогенные переменные хг и х3 — как факторы 4 и 5. Не входящая в уравнение экзогенная переменная Xj обозначается как фактор 3. В результате получим искомое уравнение

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.
Двухшаговый метод наименьших квадратов (ДМНК)
Пример 2(из Практикума.)
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 5084; Нарушение авторских прав?; Мы поможем в написании вашей работы!