Изучается модель вида

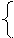y = a₁+b₁(C+D)+ε₁,

C = a₂+b₂*y+b₃*y_-1+ε₂,

где у - валовой национальный доход;

y_-1 - валовой национальный доход предшествующего года;

С - личное потребление;

D - конечный спрос (помимо личного потребления);

ε₁ и ε₂ -случайные составляющие.

Информация за девять лет о приростах всех показателей дана в табл. 3.1. (Лизер С. Эконометрические методы и задачи: Пер. с англ. - М.: Статистика, 1971. - С. 61.)

Таблица 3.1

Год	D	y-1	y	С	Год	D	y-1	y	С
	-6,8	46,7	3.1	7,4		44,7	17,8	37,2	8,6
	22,4	3,1	22,8	30,4		23,1	37,2	35,7	30,0
	-17,3	22,8	7,8	1,3		51,2	35,7	46,6	31,4
	12,0	7,8	21,4	8,7		32,3	46,6	56,0	39.1
	5,9	21,4	17,8	25,8	∑	167,5	239,1	248,4	182,7

Для данной модели с помщью МНК (функция ЛИНЕЙН или режим: Сервис, Анализ данных, Регрессия) была получена система приведенных урав­нений:

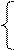y = 8,219 +0,6688 *D+0,2610*y_-1,

С = 8,636+0,3384*D+0,2020*у_-1.

Требуется:

1.Провести идентификацию модели.

2.Рассчитать параметры уравнений структурной модели.

Решение:

1. В данной модели две эндогенные переменные (у и С) и две экзогенные переменные (D и у_-1). Второе уравнение точно идентифицировано, так как содержит две эндогенные переменные и не содержит одну экзогенную переменную из системы. Иными словами, для второго уравнения имеем по счетному правилу идентификации равен­ство: 2=1+1.

Первое уравнение сверхидентифицировано, так как в нем на параметры при С и D наложено ограничение: они должны быть равны. В этом уравнении содержится одна эндогенная переменная у. Переменная С в данном уравнении не рассматривается как эндогенная, так как она участвует в уравнении не самостоятельно, а вместе с пе­ременной D. В данном уравнении отсутствует одна экзогенная переменная, имеющаяся в системе. По счетному правилу идентификации получаем: 1+1=2, т.е. D+1>H. Это больше, чем число эндогенных переменных в данном уравнении, следовательно, система сверхидентифицирована.

2. Для определения параметров сверхидентифицированной модели используется двухшаговый метод наименьших квадратов (ДМНК).

Шаг 1. На основе системы приведенных уравнений по точно идентифицированному второму уравнению определим теоретиче­ские значения эндогенной переменной С. Для этого в приведенное уравнение

С = 8,636 + 0,3384*D + 0,2020*у_-1

подставим значения D и у_-1, имеющиеся в условии задачи. Получим:

Ĉ₁= 15,8; Ĉ₂ = 16,8; Ĉ₃ = 7,4; Ĉ₄ = 14,3; Ĉ₅ = 15,0; Ĉ₆ = 27,4;

Ĉ₇ = 24,0; Ĉ₈ = 33,2; Ĉ₉ = 29,0.

C^	C^+D	Y^
15,8	9,0	7,9942
16,8	39,2	34,7206
7,4	-9,9	-0,505
14,3	26,3	18,2854
15,0	20,9	23,9174
27,4	72,1	34,9766
24,0	47,1	34,8742
33,2	84,4	49,9782
29,0	61,3	44,2438
182,7	350,2	248,4854

Шаг 2. По сверхидентифицированному уравнению структурной формы модели заменяем фактические значения С на теоретические Ĉ и рассчитываем новую переменную Ĉ + D (табл. 3.2).

Таблица 3.2

Год	D	Ĉ	Ĉ + D	Год	D	Ĉ	Ĉ + D
	-6,8	15,8	9,0		44,7	27,4	72,1
	22,4	16,8	39,2		23,1	24,0	47,1
	-17,3	7,4	-9,9		51,2	33,2	84,4
	12,0	14,3	26,3		32,3	29,0	61,3
	5,9	15.0	20,9	∑	167,5	182,9	350,4

Далее к сверхидентифицированному уравнению структурной формы модели

y = a₁+b₁(C^+D)+ε₁ применяется МНК: (обозначим новую переменную Ĉ + D через Z и решаем уравнение y = a₁+b₁*Z).

Система нормальных уравнений составит:

∑y = n*a₁+b₁*∑Z,

∑y*Z = a₁*∑Z+b₁*∑Z²,

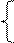248,4 = 9*a₁+350,4*b₁,

13508,71 = 350,4*a₁+21142,02*b₁.

Решая ее, получим: a₁ = 7,678; b₁ = 0,512. Итак, первое уравнение структурной модели будет таким:

У^ = 7,678 + 0,512*(С^ + D).

По данным примера получаем: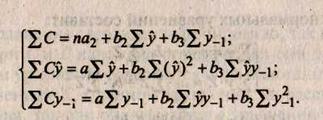

182,7=9a+248,b2+239,1b3;

6104,19 = 248,4a+8870,204b2+7204,538b3;

5301,56 = 239,1a+7204,538b2 +8375,87b3. Откуда

Соответственно второе структурное уравнение составит:

Как видим, результат совпадает с КМНК, но трудоемкость вычислений возросла.

3) Второй способ оценки параметров второго уравнения структурной модели (с помощью ДМНК):
					y = 8,219 +0,6688 *D+0,2610*y-1,
y	D	y-1	Y^	y-1	C^	b3	b2	a2
3,1	-6,8	46,7	15,86	46,7	9,31077	0,0699	0,5060	4,4767
22,8	22,4	3,1	24,01	3,1	16,23032	0,29	0,29	10,21
7,8	-17,3	22,8	2,60	22,8	10,0178	0,38	12,47	#Н/Д
21,4		7,8	18,28	7,8	15,85056	1,83		#Н/Д
17,8	5,9	21,4	17,75	21,4	14,97992	568,48	933,4	#Н/Д
37,2	44,7	17,8	42,76	17,8	24,54461
35,7	23,1	37,2	33,38	37,2	25,14212	Здесь C^= 4,4767+0,506*y+0,0699*Y-1
46,6	51,2	35,7	51,78	35,7	30,55264
	32,3	46,6	41,98	46,6	36,07122
248,4	167,5	239,1	248,40	239,10	182,70

Дата добавления: 2014-01-11