Дифференциальные уравнения равновесия жидкости в форме Эйлера

Рассмотрим условия равновесия частицы покоящейся жидкости или газа в объеме элементарного параллелепипеда с ребрами 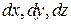, соответственно параллельными координатным осям OX, OY, OZ. Будем считать, что находящаяся в равновесии частица жидкости отвердела. Элементарный параллелепипед жидкости находится в равновесии под действием поверхностных и массовых (объемных) сил. Пусть − средние гидростатические давления на грани параллелепипеда, перпендикулярные соответствующим осям координат. При переходе от одной грани к другой давление в общем случае должно измениться, т.к. . Тогда на противоположные грани параллелепипеда, соответственно, будут действовать противодавления

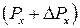, , , или иначе

, , .

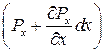Поверхностные силы, действующие по граням параллелепипеда, равны произведению среднего гидростатического давления на площадь соответствующей грани и могут быть написаны в виде:

; ;; ; ; ;

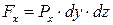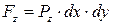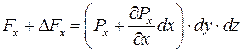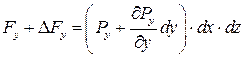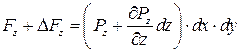Кроме поверхностных сил, на частицу жидкости будут действовать массовые (объемные) силы, распределенные по всему ее объему, т.е. действующие на каждую точку внутри элементарного параллелепипеда (например, сила тяжести, сила инерции переносного движения).

Обозначим через x, у, z − проекции массовых сил, отнесенных к единице массы m. Поскольку 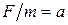, то размерность сил x, у, z соответствует размерности ускорения, т.е. [м/сек²]. Тогда проекции массовых сил могут быть написаны в виде xm, ym, zm. Учитывая, что масса частицы жидкости или газа в объеме элементарного параллелепипеда равна 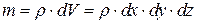, проекции массовой силы на соответствующие оси координат можно записать в виде:

; ;

;

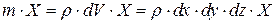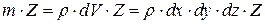Выделенный параллелепипед будет в равновесии в том случае, если сумма проекций всех действующих сил на любую из координатных осей будет равна нулю. Составим уравнение проекций сил на ось ОХ, считая, что положительное направление сил совпадает с положительным направлением осей координат:

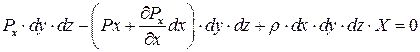или

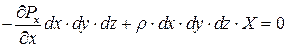
Разделим каждый член уравнения на произведение , тогда получим:

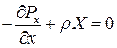
Исключение из уравнения dV означает, что вывод не зависит от объема выделенного элемента. Два другие уравнения, соответствующие условию равновесия по осям OY и OZ, напишем по аналогии.

В результате получим следующую систему уравнений статического равновесия жидкости или газа в форме Эйлера:

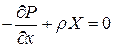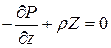, , (1)

Эти уравнения справедливы как для капельных жидкостей (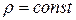), так и для газов (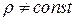). В частном случае, когда массовой силой является только сила тяжести и X=0, Y=0, Z=-g, уравнения (1) примут вид:

, , .

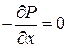Основное дифференциальное уравнение статики жидкостей и газов.

Произведем преобразование системы дифференциальных уравнений Эйлера. Умножив каждое из уравнений соответственно на 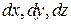, получим:

, ,

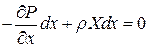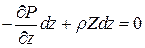
Сложив эти уравнения, получим:

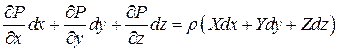
Трехчлен в левой части уравнения представляет собой полный дифференциал давления

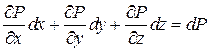
Поэтому уравнение можно записать так

(2)

Это уравнение называют основным дифференциальным уравнением статики жидкостей и газов.

В случае капельной жидкости (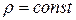) оно легко интегрируется. В случае сжимаемой жидкости (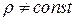) надо знать еще зависимость плотности от давления и температуры, которой может служить уравнение состояния идеального газа: .

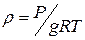Уравнение поверхности постоянного давления.

Составим уравнение поверхности равного давления. Так как в этом случае 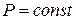, следовательно 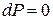. Тогда уравнение (2) примет вид:

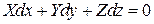
На поверхности уровня давление и плотность постоянны, следовательно, неоднородная капельная жидкость при равновесии располагается слоями одинаковой плотности: большим значениям плотности соответствуют большие значения давлений. Поверхность уровня всегда нормальна к напряжению суммарной массовой силы, действующей на жидкость при равновесии.

Закон Паскаля.

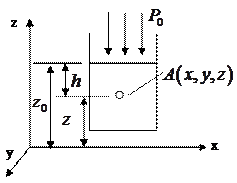Определим гидростатическое давление в произвольной точке 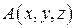жидкости с постоянной плотностью и давлением на свободной поверхности 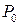. Для этого случая: , ;

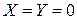Уравнение равновесия в дифференциальной форме примет вид: .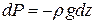

, , ,

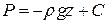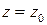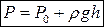или −

основное уравнение гидростатики

Выводы: Давление, с которым внешние силы действуют на граничной поверхности жидкости, передается всем частицам этой жидкости по всем направлениям без изменения величины передаваемого давления (т.е. давление жидкости не теряется в пути). Давление в любой точке складывается из давления на свободной поверхности и давления столба вышележащей жидкости. Поверхности уровня 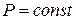параллельны свободной поверхности .

− давление столба жидкости высотой с плотностью 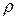на площадке 1 м². z − геометрическая высота, 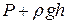− гидростатическое давление, Па,

− гидростатическая высота, м, − пьезометрическая высота.

Измерение давлений. Приборы для измерения давлений.

Пьезометрическую высоту можно наблюдать в простейшем устройстве для измерения давления который называется пьезометром. Пьезометр − вертикальная трубка, один конец которой связан с атмосферой, а другой присоединен к объему, в котором измеряется давление. − избыточное давление, − разреженное или вакуум.

Манометр. Вакуумметр.

Параметры воздуха. МСА (международная стандартная атмосфера).

Параметры воздуха зависят от многих характеристик − высоты, широты, погоды, времени года и т.д. Такие характеристики как мощность, тяга двигателей - существенно зависят от параметров воздуха. Для сравнения характеристик при различных атмосферных условиях была принята МСА − единый, условный, закон изменения давления, температуры, плотности, которая отсчитывается от уровня океана (h =0). Общеприняты так называемые нормальные атмосферные условия: 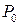=101330 Па (760 мм.рт.ст.), =288 К (15), 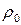=1,23 кг/м³.

В зависимости от усредненного состава и законов изменения параметров по высоте, атмосферу принято делить на следующие условные зоны:

− тропосфера − ,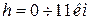

− стратосфера − ,

− химосфера − 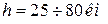, состав газа изменяется незначительно;

− ионосфера − 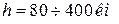, содержит ионизированный газ.

При равновесии в атмосфере действует только сила тяжести, следовательно:

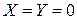, , тогда дифференциальное уравнение равновесия −

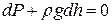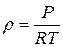, , . После преобразования получим формулы Беркеиса, для расчета параметров при изменении высоты в атмосфере:

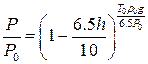, , − для тропосферы.

, − для стратосферы.

Если задана высота h, то этим по МСА, однозначно задаются параметры воздуха (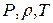). Если же задаются параметры, то по МСА однозначно определяются высота и недостающие параметры воздуха.

Кинематика жидкости и газа

Виды движения.

Причиной движения жидкости, во всех случаях, является нарушение условия ее равновесия. Задача кинематического изучения движения жидкости заключается в определении значения скорости в каждой точке движущейся жидкости для любого момента времени 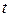. Совокупность скоростей частиц жидкой среды образует поле скоростей. Проекции составляющих скорости на прямоугольные оси координат X, Y, Z в общем случае могут быть представлены так:

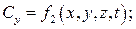
Различают два вида движения жидкости: установившееся и неустановившееся.

Установившееся движение это движение неизменное во времени, при котором параметры жидкости (скорость, давление, плотность и др.) являются функциями лишь координат и не зависят от времени, т.е. .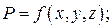

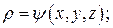
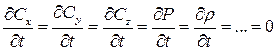(истечение жидкости из сосуда при постоянном уровне)

Неустановившееся движение это движение, при котором параметры жидкости изменяются не только с изменением координат, но и во времени, т.е.

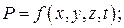
(истечение жидкости из сосуда, через отверстие в дне, при условии изменения уровня жидкости в сосуде).

Исследование движения жидкости методами Лагранжа и Эйлера.

Изучение движения жидкости можно вести двумя методами: методом Эйлера и методом Лагранжа. В обоих методах жидкость рассматривается как непрерывная среда, сплошь занимающая рассматриваемое пространство. В качестве мельчайшего элемента жидкости принимается "частица" бесконечно малых размеров, но не отождествляемая с молекулой или атомом. Вследствие этого рассматриваемая схема, неприменима к изучению молекулярных движений.

Метод Эйлера применяется для плотных жидкостей. Объектом изучения является, строго говоря, не сама жидкость, а неподвижное пространство, заполненное движущейся жидкостью; изучается изменение различных параметров, характеризующих движение в фиксированных точках пространства с течением времени, а также изменение этих параметров при переходе к другим точкам пространства. Таким образом, параметры, характеризующие движение, рассматриваются как функции координат точки и времени х, у, z, t, называемых переменными Эйлера. Например, рассматривается скорость в точке пространства, занятого движущейся жидкостью. Обозначим проекции скорости на оси координат, и для неустановившегося движения будем иметь:

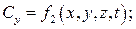
Если движение жидкости непрерывное, то для нахождения траектории жидкой частицы следует иметь в виду:

, , .

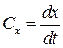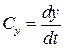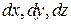− проекции элементарного перемещения на соответствующие оси координат. Проинтегрировав эти уравнения, получим уравнения траектории

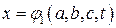и т.д., где а, b, с − начальные координаты частицы.

При неустановившемся движения все поле скоростей изменяется во времени.

Таким образом, в методе Эйлера объектами изучения являются поля, характеризующие движение (поле скоростей, поле ускорений, поле плотностей и др.).

По методу Лагранжа объектом изучения является сама движущаяся жидкость, т.е. отдельные ее частицы, рассматриваемые как материальные точки, которые сплошь заполнят некоторый движущийся объем, и изучается движение отдельных частиц жидкости вдоль их траекторий. Пусть в начальный момент координаты некоторой частицы жидкости a, b, c. У других частиц начальные координаты другие. Затем каждая частица движется по своей траектории. Текущие координаты х, у, z некоторой частицы являются функциями четырех переменных: времени t, и начальных координат a, b, c. Эти переменные называются переменными Лагранжа. Тогда:

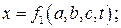
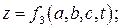
Движение жидкости вполне определено, если эта система уравнений известна. Задаваясь начальными координатами a, b, c, получим текущие координаты для выбранной частицы. Скорости частицы определяются как первые производные координаты по времени от координат х, у, z. Проекции скорости находятся из условия:

, , .

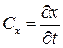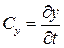Ускорения определяются как вторые производные по времени. Направления векторов скорости и ускорения находятся при помощи направляющих косинусов. Траектория любой частицы определяется непосредственно из системы уравнений путем вычисления координат х, у, z выбранной частицы для ряда моментов времени. Итак, по методу Лагранжа берется частица жидкости и исследуется движение этой частицы за промежуток времени ,.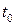

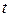Метод Лагранжа применяется в динамике разряженных сред, например, в космическом пространстве, где расстояние между молекулами газа соизмеримо с размерами летательных аппаратов и необходимо изучать движение каждое частицы в отдельности.

В ГГД плотных сред в большинстве случаев применяется более простой метод Эйлера.

Основные понятий, вводимые при изучении движения жидкости. Траектория и линия тока.

Траектория − кривая, очерчиваемая в пространстве движущейся частицей жидкости. Траектории частиц жидкости при установившемся течении являются неизменными во времени кривыми. При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, будут иметь разную форму. Для рассмотрения картины течения, образующейся в каждый момент времени, вводится понятие линии тока. Линия тока − кривая, в каждой точке которой находящаяся в ней в данный момент времени частица жидкости имеет скорость, совпадающую по направлению с касательной к этой линии. При установившемся движения линии тока с течением времени не изменяются, поэтому они совпадают с траекторией. В отличие от траектории, описанной одной частицей за некоторый промежуток времени, линия тока есть совокупность траекторий жидких частиц, векторы скоростей которых касательны к ней в данный момент времени.

В случае неустановившегося движения линии тока и траектории друг с другом не совпадают. Частица жидкости в момент t, прошедшая через отверстие сосуда, который опорожняется (движение неустановившееся), в дальнейшем в разные моменты времени будет принадлежать различным струям. Траектория частицы пересекает семейство струек.

Элементарная струйка.

Замкнутая поверхность, составленная из линий тока, называется трубкой тока. Часть жидкости, ограниченная трубкой тока, называется элементарной струйной. Элементарная струйка обладает следующими свойствами: 1) в случае установившегося движения форма элементарной струйки остается неизменной во времени, так как вид линий тока, из которых состоит струйка, в установившемся движении во времени не меняется; 2) поверхность элементарной струйки является непроницаемой для частиц жидкости, движущихся в соседних струйках, поскольку на поверхности струйки векторы скорости частиц совпадают с касательными. Таким образом, элементарная струйка представляет собой как бы самостоятельный элементарный поток. Поперечное сечение элементарной струйки принимается бесконечно малым: 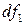, 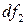. Вследствие этого скорости во всех точках ее поперечного сечения одинаковые. При решении многих задач гидродинамики делается предположение о том, что поток движущейся жидкости состоит из отдельных элементарных струек. Течение такого потока называют струйным, вследствие различия скоростей соседние струйки будут скользить одна по другой, не перемешиваясь друг с другом.

Расход жидкости. Средняя скорость.

Живым сечением потока называется элементарная площадка нормальная к вектору скорости .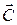

Объемным расходом жидкости 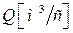называется объем жидкости, протекающий через данную поверхность в единицу времени.

Массовым расходом жидкости называется масса жидкости, протекающий через данную поверхность в единицу времени. Если 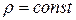, то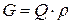

Среднерасходная скорость − постоянная для всего поперечного сечения потока и равна скорости, при которой расход равен действительному.

; ;

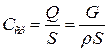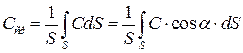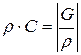− плотность тока − масса жидкости, протекающая через 1 м² сечения за 1 с, или массовый расход через площадку 1 м².

Дата добавления: 2014-01-11