В форме Навье-Стокса

Дифференциальные уравнения движения вязкой жидкости

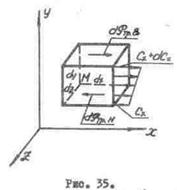Дифференциальные уравнения движения вязкой жидкости в общем виде значительно сложнее уравнений движения идеальной жидкости, так как влияние вязкости сказывается не только в появлении касательных напряжении, но и в изменении величины нормального давления. Для их составления выделим в прямоугольной системе координат в потоке жидкости у точки M (x, y, z) элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка М была одной из его вершин. Выражения для массы элемента, проекций его ускорения на оси координат, проекций объемных сил запишутся здесь так же, как и при выводе уравнений движения идеальной жидкости в форме Эйлера. Отличие будет только в выражениях для поверхностных сих. В случае вязкой жидкости на грани параллелепипеда будут действовать не только нормальные напряжения 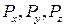, но и касательные, потому что поверхностные силы в вязкой жидкости не ортогональны к рассматриваемой поверхности. В уравнения движения вязкой жидкости, помимо ускорений, учитываемых при движении идеальной жидкости, должны войти еще и ускорения от сил трения. Посмотрим сначала, как следует учитывать ускорения от сил трения при плоскопараллельном движении жидкости вдоль оси X с градиентом скорости только в направлении оси Y.

Согласно гипотезе Ньютона, при слоистом (ламинарном) течении жидкости сила трения между ее слоями равна

,

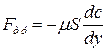где 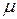− динамический коэффициент вязкости; 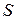− площадь поверхности трения; 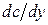− градиент скорости по нормали y. Силу трения, отнесенную к единице площади поверхности трения, обозначают через 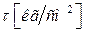и называют напряжением трения. Итак,

.

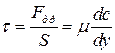При наличии градиента скорости вдоль оси Y силы трения на верхнюю и нижнюю грани параллелепипеда действуют в противоположных направлениях. Сила трения на нижней грани элемента определяется как

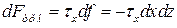
на верхней грани элемента, где напряжение трения 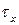получило приращение , она равна .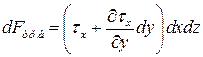

Равнодействующая сила трения, действующая на жидкий элемент в направлении оси X, будет определяться разностью сил, действующих на нижней и верхней гранях элемента

.

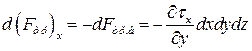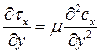Так как согласно гипотезе Ньютона, и , то

.

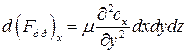Соответствующее ускорение, т.е. силу трения, приходящуюся на единицу массы элемента 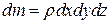, можно выразить как

.

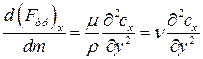В трехмерном потоке, когда градиенты скорости могут существовать в направлении всех трех координатных осей, ускорение от сил трения в проекциях на оси X, Y, Z, выражаются следующим образом:

, ,

.

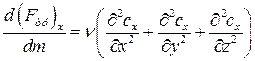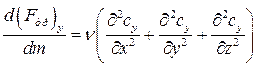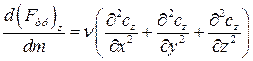Эти проекции ускорений от сил трения следует ввести в дифференциальное уравнения движения вязкой жидкости помимо ускорений, действующих на частицу идеальной жидкости. Тогда дифференциальные уравнения движения вязкой жидкости запишутся в виде:

,

, (*)

.

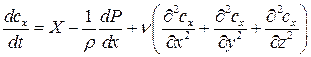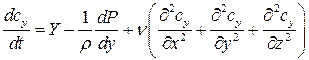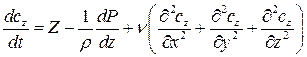Уравнения движения, записанные в такой форме (*), называются уравнениями Навье-Стокса для вязкой несжимаемой жидкости. Если при изучении движения вязкой жидкости одновременно учитывать и сжимаемость, то уравнения движения будут более сложными.

При движении вязкой (реальной) жидкости за гидростатическое давление в точке принимают среднее арифметическое значение давлений по трем произвольным, проходящим через данную точку, взаимно перпендикулярным площадкам, т.е.

.

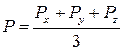Все слагаемые в уравнениях Навье-Стокса, так же как и в уравнениях Эйлера, имеет размерность ускорения м/сек². В левые части уравнений входят проекция полного ускорения частицы, в правые части − проекции ускорения от объемных сил, от сил давления и от сил вязкости (трения). Неизвестными величинами являются скорости 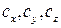, давление Р, и в общем случав сжимаемой жидкости плотность 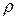. Зависимость 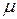от температуры считается известной. Для того чтобы получилась замкнутая система уравнений, в которой число уравнений равнялось числу неизвестных, необходимо к уравнениям Навье-Стокса присоединить уравнение неразрывности движения

,

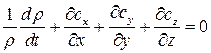а в случае сжимаемой жидкости, еще и характеристическое уравнение .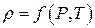

Дата добавления: 2014-01-11