Тема 4. Правила построения индексов

4.1. Понятие и виды индексов

4.2. Средний арифметический и средний гармонический индексы

4.3. Индексы средних показателей

4.1. В статистическом анализе большое внимание уделяется использованию индексного метода. Индекс − это относительный показатель, позволяющий анализировать изменение социально-экономического явления во времени и в пространстве, а также оценивать степень выполнения плана.

В зависимости от используемой базы сравнения различают динамические и территориальные индексы. Динамические индексы отражают изменение явления во времени, а территориальные индексы используются для пространственных сопоставлений различных показателей.

В зависимости от способа построения различают индивидуальные и общие (сводные, агрегатные) индексы.

Индивидуальный индекс − это результат сравнения двух значений показателя, характеризующего простое социально-экономическое явление. Примерами индивидуального индекса могут служить:

- индивидуальный индекс цен:

,

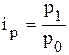где 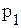,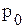- цена продукции соответственно в отчетном и базисном периодах;

- индивидуальный индекс физического объема реализации:

,

где ,- физический объем реализации соответственно в отчетном и базисном периодах;

- индивидуальный индекс товарооборота:

,

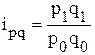где , 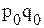- товарооборот соответственно в отчетном и базисном периодах.

Между индивидуальными индексами существует взаимосвязь, определяемая следующим соотношением:

.

Общий (сводный, агрегатный) индекс − это результат сравнения двух значений показателя, характеризующего сложное социально-экономическое явление. Общий индекс состоит из двух элементов: индексируемой величины и соизмерителя, называемого весом. Примерами общего индекса могут служить:

- общий индекс цен:

.

Индексируемой величиной в данной формуле является цена , а весом − физический объем реализации в отчетном периоде 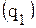. Числитель формулы представляет собой реальный товарооборот в отчетном периоде, а знаменатель − условный товарооборот в отчетном периоде в ценах базисного периода. Разность между числителем и знаменателем общего индекса цен позволяет определить изменение товарооборота за счет изменяющихся цен:

,

а разность между знаменателем и числителем общего индекса цен позволяет определить экономию (перерасход) денежных средств потребителя в результате снижения (повышения) цен:

;

- общий индекс физического объема реализации:

.

Индексируемой величиной в данной формуле является физический объем реализации 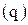, а весом − цена в базисном периоде . Знаменатель формулы представляет собой реальный товарооборот в базисном периоде. Разность между числителем и знаменателем общего индекса физического объема реализации позволяет определить изменение товарооборота за счет изменяющегося физического объема реализации:

;

- общий индекс товарооборота:

.

Индексируемой величиной в данной формуле является товарооборот 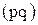, а вес равен единице. Разность между числителем и знаменателем общего индекса товарооборота позволяет определить общее изменение товарооборота в отчетном периоде по сравнению с базисным под действием всех факторов:

.

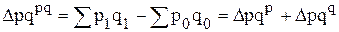Между общими индексами существует взаимосвязь, определяемая следующим соотношением:

.

По рассмотренной схеме можно построить индивидуальные и общие индексы для любой системы трех показателей. Например, для системы показателей − себестоимость продукции , физический объем производства 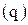и производственные затраты , индивидуальные и общие индексы будут иметь вид:

, , ,

, , .

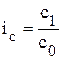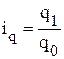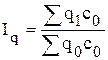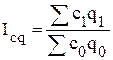Для построения общих индексов необходимо руководствоваться следующим правилом:

- если индексируемой величиной является качественный показатель (цена, себестоимость, производительность труда, урожайность и т.д.), то для построения общего индекса вес выбирается на уровне отчетного периода;

- если индексируемой величиной является количественный (объемный) показатель (физический объем реализации, физический объем производства, посевная площадь и т.д.), то для построения общего индекса вес выбирается на уровне базисного периода.

Общие индексы, в которых используется вес отчетного периода, называются индексами Пааше, а общие индексы, в которых используется вес базисного периода, называются индексами Ласпейреса.

Если известны данные об изучаемом социально-экономическом явлении за несколько периодов, то может быть построен ряд цепных и базисных индексов. Базисные индексы имеют постоянную базу сравнения, а цепные индексы − переменную базу сравнения. Цепные и базисные индексы могут быть построены как для индивидуальных, так и для общих индексов.

Примерами цепных индивидуальных индексов могут служить:

- цепные индивидуальные индексы цен:

, ,..., ;

- цепные индивидуальные индексы физического объема реализации:

, ,..., ;

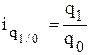- цепные индивидуальные индексы товарооборота:

, ,..., .

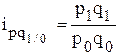Примерами базисных индивидуальных индексов могут служить:

- базисные индивидуальные индексы цен:

, ,..., ;

- базисные индивидуальные индексы физического объема реализации:

, ,..., ;

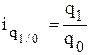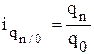- базисные индивидуальные индексы товарооборота:

, ,..., .

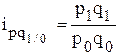Между цепными и базисными индивидуальными индексами существует взаимосвязь, определяемая следующими соотношениями:

;

;

.

Цепные и базисные общие индексы могут иметь постоянные и переменные веса.

Примерами цепных общих индексов могут служить:

- цепные общие индексы цен с постоянными весами:

, ,..., ;

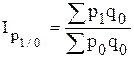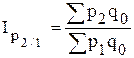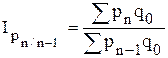- цепные общие индексы цен с переменными весами:

, ,..., ;

- цепные общие индексы физического объема реализации с постоянными весами:

, ,..., ;

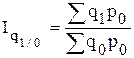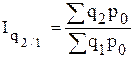- цепные общие индексы физического объема реализации с переменными весами:

, ,..., ;

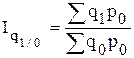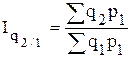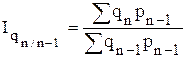- цепные общие индексы товарооборота:

, ,..., .

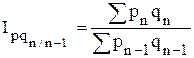Примерами базисных общих индексов могут служить:

- базисные общие индексы цен с постоянными весами:

, ,..., ;

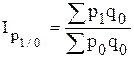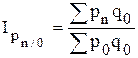- базисные общие индексы цен с переменными весами:

, ,..., ;

- базисные общие индексы физического объема реализации с постоянными весами:

, ,..., ;

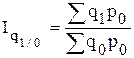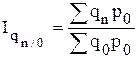- базисные общие индексы физического объема реализации с переменными весами:

, ,..., ;

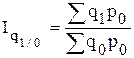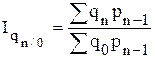- базисные общие индексы товарооборота:

, ,..., .

Между цепными и базисными общими индексами с постоянными весами существует взаимосвязь, определяемая следующими соотношениями:

;

;

.

4.2. Для определения общих индексов в некоторых случаях целесообразно их представить в форме средних арифметических или средних гармонических индексов. Например:

- средний арифметический индекс цен имеет вид:

.

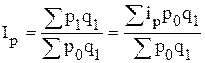Усредняемой величиной в данной формуле является индивидуальный индекс цен, а весом − условный товарооборот отчетного периода.

- средний гармонический индекс цен имеет вид:

.

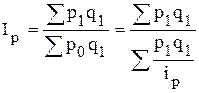Усредняемой величиной в данной формуле является индивидуальный индекс цен, а весом − реальный товарооборот отчетного периода.

- средний арифметический индекс физического объема реализации имеет вид:

.

Усредняемой величиной в данной формуле является индивидуальный индекс физического объема реализации, а весом − реальный товарооборот базисного периода.

- средний гармонический индекс физического объема реализации имеет вид:

.

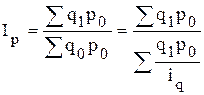Усредняемой величиной в данной формуле является индивидуальный индекс физического объема реализации, а весом − условный товарооборот отчетного периода.

Выбор той или иной формы среднего индекса зависит от того, какие исходные данные имеются в распоряжении исследователя при решении конкретных задач.

4.3. При изучении различных социально-экономических явлений часто приходится рассматривать динамику изменения средней величины индексируемого качественного показателя. Значение среднего показателя определяется влиянием, как индексируемой величины, так и веса. Для анализа динамики среднего показателя используется следующая система взаимосвязанных индексов:

- индекс переменного состава характеризует динамику среднего показателя, как под действием индексируемой величины, так и под действием веса:

,

где 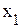, - значение индексируемого качественного показателя соответственно в отчетном и базисном периодах;

, - вес индексируемого качественного показателя соответственно в отчетном и базисном периодах;

- индекс фиксированного (постоянного) состава характеризует динамику среднего показателя только под действием индексируемой величины:

;

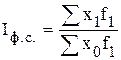- индекс структурных сдвигов характеризует динамику среднего показателя только под действием изменения веса индексируемой величины:

.

Например, для анализа динамики средней цены определяются:

- индекс цен переменного состава:

;

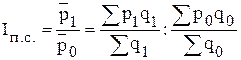- индекс цен фиксированного (постоянного) состава:

;

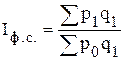- индекс структурных сдвигов применительно к ценам:

.

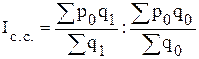Дата добавления: 2014-01-11