Тема 4. Поняття інтеграла. Знаходження площ

У попередній темі визначили поняття похідної, яка вимірювала швидкість зміни функції. В деяких випадках, замість починати з функції f і знаходити швидкість зміни функції f^’, починають з функції f, яка вже описує швидкість зміни функції і знаходять функцію F таку, що F^’=f. Ця операція є зворотньою до обчислення похідної. Таким чином визначена функція F називається первісною.

Якщо f і F функції такі, що

F^’(x)=f(x)

для всіх значень x з області визначення f, то F(x) називають первісною функції.

Приклад 16. Нехай f(x)= 2x+3 і F(x)=x²+3x. Тоді F(x) є первісною для функції f(x), бо

F^’(x)=(x²+3x)^’=2x+3=f(x)

для всіх значень x. Розглянемо більш загальну функцію G(x)=x²+3x+C, де С – довільна стала. Похідна цієї функції рівна

G^’(x)=(x²+3x+C)^’=2x+3=f(x)

для всіх значень x. Тому, G(x) теж є первісною для функції f(x). Отже, функція f(x) має багато первісних і всі вони виду

G(x)=x²+3x+C.

Звідси видно, що первісні функції відрізняються на сталу.

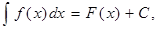Неозначеним інтегралом функції f називають сукупність всіх первісних функції f

де F(x) – довільна первісна функції f(x), а С – стала.

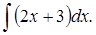Приклад 17. Знайдемо

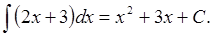Оскільки F(x)=x²+3x є первісною для функції f(x)=2x+3, то

Визначемо неозначені інтеграли для деяких функцій

Таблиця найпростіших інтегралів

При інтегрування користуються наступними правилами

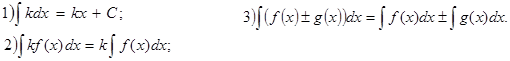
Основні правила інтегрування

Приклад 18. Знайти інтеграли

Деякі інтеграли знаходяться за допомогою заміни змінних.

Приклад 19. Знайти інтеграл

Для його знаходження проведемо заміну y=3x+1. Тоді

dy=(3x+1)’dx=3dx,

або

dx=dy/3.

Проведемо в інтегралі заміну x на y і отримаємо

Якщо f(x) та g(x) деякі функції, то похідна добутку цих функцій рахується за формулою

(f(x)g(x))^’=f^’(x)g(x)+f(x)g^’(x).

Звідси,

f(x)g^’(x)=(f(x)g(x))^’-f^’(x)g(x).

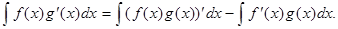Проінтегруємо дану рівність

Оскільки обчислення похідної та інтегрування є обернені операції, то дві ці операції, проведені одна за другою, компенсують дію одна одної. Тому,

і ми отримуємо формулу інтегрування по частинах, яка має вигляд

Приклад 20. Знайдемо інтеграл

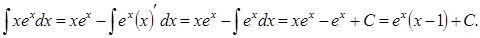Тут f(x)=x, g’(x)=e^x, а g(x)=e^x. Тому,

Поняття означеного інтеграла функції на проміжку є дуже важливим. Означеним інтегралом функції на проміжку називають число, яке виражає загальну зміну деякої первісної функції на проміжку. Для прикладу, якщо

f(x)=2x+1,

то довільна первісна цієї функції має вигляд

F(x)=x²+x+C.

Загальна зміна функції F(x) на інтервалі [1,3] дорівнює

F(3)-F(1)=(3²+3+C)-(1²+1+C)=12-2=10.

Тому, кажуть, що означений інтеграл функції f(x) на інтервалі [1,3] дорівнює 10. Зауважимо, що при обчисленні означеного інтеграла ми використовували довільну первісну, бо константа при відніманні скорочується. Тому, константа не використовується при обчисленні означеного інтеграла.

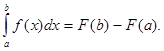Отже, якщо f позначає функцію, визначену на інтервалі [a,b], то означений інтеграл, що виражає загальну зміну первісної для функції f(x) на проміжку, дорівнює

Числа a і b називають межі інтегрування (відповідно нижня і верхня).

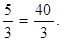Приклад 21. Обчислимо означений інтеграл

Приклад 22. Функція граничних витрат фірми задана рівнянням

MC(x)=2x²-8x+30.

Зараз фірма випускає 6 одиниць на день. Які будуть додаткові витрати, якщо фірма вирішить виготовляти 10 одиниць на день?

Оскільки граничні витрати це показник зміни витрат, то загальна зміна витрат від збільшення виробництва від x=6 до x=10 одиниць рівна

Отже, змінивши обсяги виробництва з 6 одиниць до 10 одиниць, фірма матиме додаткові витрати $386, 67.

Розглянемо одне з найважливіших застосувань означеного інтеграла – обчислення площ заданих фігур. Нехай f позначає неперервну і невід’ємну на проміжку [a,b] функцію. Графік даної функції зображено на мал.22.

Розглянемо область, обмежену графіком функції f, вісю x, прямими x=a та x=b. Ця область має площу, яку називають площа під функцією f(x) на проміжку [a,b]. Між площею та означеним інтегралом існує зв’язок, виражений формулою

Приклад 23. Нехай f(x)=x. Знайдемо площу під f(x) на проміжку [0,1]. Як видно з мал. 23, фігурою, площу якої треба знайти, є трикутник.

Знайдемо площу за допомогою означеного інтеграла:

Отже, площа трикутника дорівнює ½.

Якщо графік функції f лежить під вісю x на проміжку [a,b], то означений інтеграл

буде від’ємним числом. У цьому випадку площа області, що лежить між графіком функції, вісю x, прямими x=a та x=b, дорівнює абсолютному значенню означеного інтеграла.

На мал.24 показано ситуацію, коли f(x) на проміжку [a,b] є від’ємною. Тому, площа між графіком функції f(x), вісю х, прямими x=a та x=b, знаходимо за формулою

Вважаючи, що означений інтеграл є площею, розглянемо

властивості означеного інтеграла:

(бо площа під графіком функції f(х) на проміжку [a,a] дорівнює 0);

(бо площа під графіком функції f(x) на проміжку [a,b] дорівнює сумі площ під f(x) на відрізку [a,c] та на проміжку [c,b], де a<c<b).

На мал.25 зображено область, обмежена графіками двох функцй f(x) та g(x). Площу такої області визначають, як площу між кривими f та g.

Для визначення площі між двома кривими f(x) та g(x) треба:

- прирівняти f(x)=g(x), розв’язати рівняння, щоб знайти x=a та x=b;

- площу знаходимо за формулою

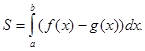Приклад 25. Знайдемо площу області, обмежену прямими y=2-x, y=x-2, x=0. Для знаходження потрібної площі, намалюємо графіки потрібних функцій

На мал.26 зображено графіки функцій, що обмежують область. Як видно з малюнка, потрібно визначити площу виділеного трикутника. Ліва межа області – це відрізок АС, а права – точка В. Знайдемо координати точки В, як точки перетину прямих y=x-2 та y=2-х. Для цього прирівняємо праві частини цих функцій

x-2=2-x.

Звідки,

х=2.

Оскільки відрізок АС є частиною прямої х=0, а точка В має першу координату х=2, то площу області знаходимо на відрізку [0,2]. Верхня межа трикутника – це відрізок АВ, що є частиною прямої y=2-x, а нижня межа – відрізок ВС, частина прямої y=x-2. Тому площу виділеного трикутника знайдемо за формулою

Отже, шукана площа рівна 4 кв.од.

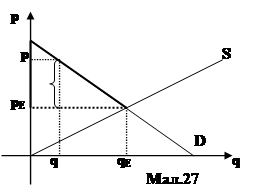За допомогою означеного інтеграла дуже зручно обчислювати такі економічні поняття, як споживчий та виробничий надлишок. Для визначення цих понять розглянемо функції попиту та пропозиції на мал.27.

На ринку встановилася ринкова рівновага. Тобто, при ціні p_E за одиницю продукції виробники продають q_E одиниць продукції. Припустимо, що покупець хоче купити q одиниць по ціні p. Але на ринку вже встановлена ціна p_E<p. Отже, покупець отримає додаткову вигоду розміром (p-p_E)q. Сукупний споживчий надлишок буде рівна площі виділеного трикутника на мал.27, яку обчислюємо за формулою

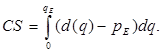Аналогічно встановлюємо формулу для обчислюємо сукупного виробничого надлишку

Приклад 26. Припустимо, що функція пропозиції на продукцію задана формулою

s(q)=0,009q²,

а функція попиту – рівнянням

d(q)=30-0,003q².

Для обчислення споживчого та виробничого надлишку треба знайти ціну та кількість ринкової рівноваги. Для цього прирівняємо функції попиту та пропозиції і розв’яжемо рівняння

0,009q²=30-0,003q²,

або

0,012q²=30

і

q²=30/0,012=2500.

Звідси,

q=q_E=50,

а p_E=s(q_E)=d(q_E)=0,009*50²=22,50. Тому,

Дата добавления: 2014-01-11