Тема 5. Фінансова математика

У цій темі розглянемо застосування математики в фінансах, а саме поняття простого та складного процента, процента, що нараховується кілька разів на рік, визначення теперішньої та майбутньої вартості інвестицій.

Нехай P₀ позначає початкову суму інвестиції, r – річну процентну ставку (r=i/100), P – кінцеву суму інвестиції. Простий процент нараховується від початкової суми, а складний – від тої, яка є на даний момент. Розглянемо формули нарахування простого та складного процентів.

	Простий процент	Складний процент
Кінець першого року	P1=P0+P0r або P1=P0(1+r)	P1=P0+P0r або P1=P0(1+r)
Кінець другого року	P2=P1+P0r або P2=P0(1+2r)	P2=P1+P1r або P2=P0(1+r)^2
........	........	.......
Кінець n-ого року	Pn=P0(1+nr)	Pn=P0(1+r)^n

Приклад 27. Припустимо, що ви інвестуєте $100 на 5 років під 12% річних (простий процент нарахування). Яка сума буде на рахунку в кінці терміну?

За формулою нарахування простого процента P₅=P₀(1+5r) =100(1+5*0,12)=$160. Отже, інвестиція в $100 зросте через 5 років до $160.

Приклад 28. Припустимо, що ви інвестуєте $100 на 5 років з простим процентом нарахування, і плануєте отримати кінцеву суму $130. Якою в цьому випадку повинна бути річна процентна ставка?

В цій задачі P₀=$100, n=5, P₅=$130, а потрібно знайти коефіцієнт r. З формули нарахування простого процента

r=(P_n/P₀-1)/n.

Тому, коефіцієнт r в даній задачі дорівнює

r=(130/100-1)/5=0,3/5=0,06,

або 6%.

Приклад 29. Річна процентна ставка становить 8,25%. Скільки потрібно інвестувати сьогодні, щоб через один рік отримати $411,350?

Оскільки інвестиція терміном на один рік, то не має значення який процент нарахування – простий чи складний. В задачі відомі r=0,0825, n=1, P₁=$411,350, а потрібно знайти P₀. З формули нарахування процента

P₀=P₁/(1+r).

Тому, початкова сума дорівнює

P₀=411,350/(1+0,0825), або $380.

Іноді процент нараховується кілька разів на рік. Такий процент називається компанований. Нехай, для прикладу, процент нараховується щоквартально (4 рази на рік). Річна процентна ставка r ділиться на чотири частини і щокварталу процентна ставка нарахування становить r/4. Тоді розподіл кінцевих сум в залежності від кварталу та процента нарахування отримаємо з таблиці

	Простий процент	Складний процент
Перший квартал	P1/4=P0(1+r/4)	P1/4=P0(1+r/4)
Другий квартал	P2/4=P0(1+2r/4)	P2/4=P0(1+r/4)^2
Третій квартал	P3/4=P0(1+3r/4)	P1/4=P0(1+r/4)^3
Четвертий квартал (кінець першого року)	P4/4=P0(1+4r/4)=P0(1+r)	P4/4=P0(1+r/4)^4

Як видно з таблиці, що для простого процента не має значення скільки разів на рік нараховується процент. Сума в кінці року залишається одинаковою P₀(1+r). Іншу ситуацію маємо для складного процента. В цьому випадку кінцева сума, якщо процент нараховується один раз на рік, становить P₀(1+r), і не дорівнює кінцевій сумі у випадку, якщо процент нараховується чотири рази на рік, яка рівна P₀(1+r/4)⁴.

Визначимо загальну формулу знаходження кінцевої суми, якщо інвестовано P₀ з річною процентною ставкою r і проценти нараховуються m разів на рік. При таких умовах в кінці першого року ми отримаємо на рахунку

P₁=P₀(1+r/m)^m.

Для визначення кінцевої суми через t років маємо формулу

P_t=P₀(1+r/m)^mt,

бо t років містять mt періодів нарахування процентів.

Приклад 30. Чотири банки мають одинакову річну процентну ставку 8%, але нарахування проходить по-різному: перший банк нараховує проценти щоквартально, другий банк – щомісячно, третій – щотижнево, а четвертий – щоденно (360 днів на рік). Визначити, яка сума буде на рахунку в кінці року в кожному банку, якщо на початку року інвестувати $1000.

Оскільки перший банк нараховує 4 рази на рік проценти, то в кінці першого року на рахунку буде сума розміром

P_4/4=$1000(1+0,08/4)⁴=$1082,43.

Аналогічно на рахунку в другому банку буде сума

P_12/12=$1000(1+0,08/12)¹²=$1083,

в третьому банку

P_52/52=$1000(1+0,08/52)⁵²=$1083,22,

в четвертому банку

P_360/360=$1000(1+0,08/360)³⁶⁰=$1083,28.

Як видно з розв’язку задачі, що при однаковій процентній ставці кінцева сума на рахунку зростає зі зростанням кількості нарахувань процентів на рік. Тобто, чим частіше на рік нараховуються проценти, тим більшою буде кінцева сума.

Попередні приклади наводилися у випадку, коли інвестиції розраховані на один рік. Загальна формула нарахування кінцевої суми після k компанованих періодів має вигляд

P_k/m=P₀(1+r/m)^k.

Ця формула справедлива як для k<m, так і для k≥m.

Приклад 31. Обчислити кінцеву суму на рахунку, якщо інвестувати $100 на 2,5 роки під 12% річних, що нараховуються щоквартально.

Кінцеву суму знайдемо з формули

P=P₀(1+r/4)^4*2,5=$100(1+0,12/4)¹⁰=$134,39.

Приклад 32. Розглянемо річну процентну ставку 12%, що нараховується щопіврічно. Скільки треба інвестувати сьогодні, щоб через 5 років отримати $1000.

Шукану cуму знайдемо з формули

P₀=P/((1+r/2)^2*5)=$1000/((1+0,12/2)¹⁰)=$558,39.

Cуму P=P₀(1+r/m)^mt називають майбутньою вартістю (через t років) інвестиції розміром P₀. Подібно, суму P₀=P/(1+r/m)^mt називають теперішньою вартістю грошей розміром P (через t років). Можна ввести наступні поняття: майбутньою вартістю грошей (FV) називають суму, яку отримаємо на рахунку через t років, інвестувавши сьогодні cуму розміром P₀; теперішньою вартістю грошей (PV) називають суму, яку треба інвестувати сьогодні, щоб через t років отримати суму розміром P. У прикладі 31 ми знайшли майбутню вартість інвестованих $100 через 2,5 роки. В прикладі 32 знайдено було теперішню вартість $1000 (протягом 5 років).

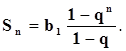До сих пір ми розглядали випадки разових інвестицій. Однак, часто інвестори роблять кілька депозитів, або отримують кілька виплат – через рівні проміжки часу. Таке поняття визначене в фінансах, як анюїтет. Анюїтет – це регулярні одинакові платежі або виплати. В цьому випадку кінцева сума буде складатися з кількох частин, кожна є яких відноситься до одного депозиту. Утворена сума являє собою суму геометричної прогресії і для її визначення використовують формулу (b₁ – перший елемент прогресії, q – знаменник прогресії, S_n – сума n перших членів геометричної прогресії)

Приклад 33. Припустимо, що в кінці кожного місяця протягом року ви інвестуєте $1000 під 6% річних, що нараховуються щомісячно. Яка сума буде на рахунку в кінці року?

Оскільки в кінці кожного місяця інвестується сума розміром $1000, то кожна така сума приносить певний дохід (в залежності від того скільки разів нараховувалися проценти на цю суму). Розподіл початкових інвестицій та їх кінцеві суми по окремих місяцях видно з таблиці

Дата інвестиції	Інвестована сума	Кількість нарахувань процентів протягом року	Кінцева сума окремої інвестиції
31 січня	$1000		$1000(1+0,06/12)^11
28 лютого	$1000		$1000(1+0,06/12)^10
......	.......	..........	............
31 грудня	$1000		$1000(1+0,06/12)^0

Загальна кінцева сума таких інвестицій становить суму кінцевих рахунків по всіх місяцях

P=$1000(1+0,005)⁰+…+$1000(1+0,005)¹⁰+$1000(1+0,005)¹¹.

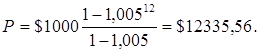Ця сума є сумою 12 членів геометричної прогресії з першим елементом b₁=$1000, знаменником q=1+0,005=1,005. За формулою суми геометричної прогресії

Отже, інвестуючи щомісяця $1000 під 6% річних, що нараховуються щомісячно, в кінці року ми отримаємо $12335,56, що є на $335,56 більше, ніж ми б просто складали гроші, не інвестуючи їх.

Подібно можна визначити теперішню вартість всіх 12 депозитів.

Приклад 34. Розглянемо умову прикладу 33. Але тут знайдемо теперішню вартість.

Теперішня вартість k-ого депозиту становить 1000/(1,005)^k. Отже, загальна теперішня вартість 12 депозитів становить

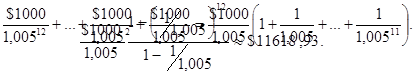Cума в дужках теж є сумою 12 елементів геометричної прогресії з b₁=1, q=1/1,005 і тому рівна

Отже, щоб отримувати в кінці кожного місяця протягом року по $1000 треба на початку року внести $11618,93.

Іноді потрібно визначити величину анюїтету при відомих теперішній та майбутній вартостях та терміну інвестиції. Розглянемо приклад, в якому показано як визначити невідомий анюїтет.

Приклад 35. Припустимо, що ви купляєте будинок, вартістю $250000, в кредит на 30 років під 12% річних, що нараховуються щомісячно. Яку суму вам потрібно виплачувати в кінці кожного місяця, щоб виплатити вартість кредиту та нараховані на нього проценти?

Знайти місячні виплати можна, прирівнявши вартість кредиту, в цьому прикладі $250000, і теперішню вартість всіх місячних виплат. Для зручності позначимо ще не відому величину щомісячних виплат через p. Тоді

$250000=теперішній вартості всіх 360 (30 років по 12 місяців) місячних виплат р

Взявши до уваги початок та кінець рівності, отримаємо

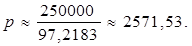
Тобто, місячні виплати становлять $2571,53.

Дата добавления: 2014-01-11