
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные понятия теории кодирования
|
|
|
|
Вообще говоря, кодирование - любое преобразование сообщения в сигнал путем установления взаимного соответствия между ними. В узком смысле кодирование – преобразование дискретного сообщения в последовательность кодовых символов по заданному правилу. Множество всех кодовых последовательностей (кодовых комбинаций или слов), возможных при данном правиле кодирования, образует код. Правило кодирования можно выразить кодовой таблицей с алфавитом кодируемых сообщений и соответствующими им кодовыми комбинациями. Совокупность символов, из которых составляют кодовые последовательности, называют кодовым алфавитом, а их число 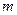 (объем кодового алфавита) – основанием кода.
(объем кодового алфавита) – основанием кода.
Правила кодирования 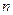 элементов сообщения - правила записи
элементов сообщения - правила записи 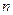 различных чисел в
различных чисел в 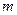 -ичной системе счисления. Различают двоичные (
-ичной системе счисления. Различают двоичные (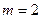 ) и многопозиционные (
) и многопозиционные (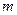 -ичные,
-ичные, 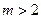 ) коды. Длина кодового слова
) коды. Длина кодового слова 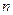 - число разрядов в нем. Для передачи сообщений в двоичном коде достаточно иметь лишь два разных сигнала. Так, символы
- число разрядов в нем. Для передачи сообщений в двоичном коде достаточно иметь лишь два разных сигнала. Так, символы 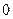 и
и 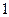 можно передать колебаниями разных частот или импульсами тока разной полярности. Расстояние Хэмминга
можно передать колебаниями разных частот или импульсами тока разной полярности. Расстояние Хэмминга 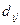 между двумя кодовыми словами
между двумя кодовыми словами 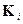 и
и 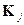 находят в два этапа. Складывают поразрядно искомые слова в
находят в два этапа. Складывают поразрядно искомые слова в 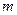 -ичной системе счисления без переноса в старший разряд (сложение по модулю основания кода
-ичной системе счисления без переноса в старший разряд (сложение по модулю основания кода 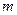 , обозначаемое символом ²
, обозначаемое символом ² ²). Полученные значения складывают в
²). Полученные значения складывают в 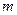 -ичной системе счисления:
-ичной системе счисления:
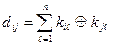 , (1.1)
, (1.1)
где  и
и 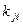 - одноименные (
- одноименные (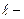 ые) разряды кодовых слов
ые) разряды кодовых слов 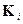 и
и 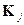 , соответственно. Так,
, соответственно. Так, 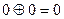 ,
, 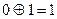 ,
, 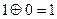 и
и 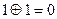 при
при 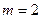 . Для двоичного кода расстояние
. Для двоичного кода расстояние 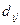 равно числу разрядов, в которых слова
равно числу разрядов, в которых слова 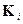 и
и 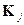 различны. Кодовое расстояние
различны. Кодовое расстояние 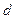 - наименьшее для данного кода значение
- наименьшее для данного кода значение 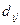 . В эквидистантном коде расстояния между двумя любыми его словами одинаковы. Число ненулевых элементов кодового слова равно его весу
. В эквидистантном коде расстояния между двумя любыми его словами одинаковы. Число ненулевых элементов кодового слова равно его весу 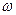 .
.
1.2. Классификация методов кодирования
На рис. 1.1 дана классификация методов кодирования  . Одна из его задач - согласование алфавита сообщения с алфавитом канала. Каждый ансамбль сообщений можно кодировать разными способами. Лучший код удовлетворяет требованиям:
. Одна из его задач - согласование алфавита сообщения с алфавитом канала. Каждый ансамбль сообщений можно кодировать разными способами. Лучший код удовлетворяет требованиям:
1) приемник может восстановить сообщение источника, посланное по линии связи;
2) для представления одного сообщения в среднем нужно минимальное число символов.
Первому требованию удовлетворяют обратимые коды. В них все кодовые слова различны и однозначно связаны с соответствующими сообщениями. Экономные коды удовлетворяют второму требованию.
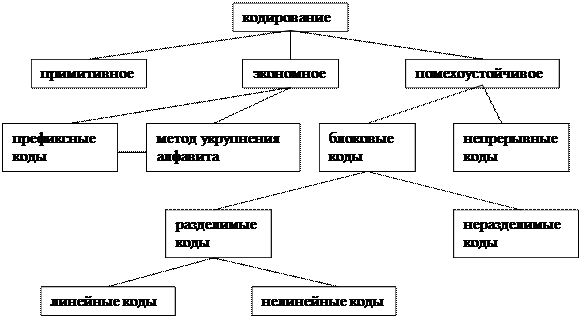 |
Рис. 1.1. Классификация методов кодирования
Целью эффективного (статистического) кодирования является повышение скорости передачи информации и приближение этой скорости к максимально возможной - пропускной способности канала связи. Согласование производительности источника сообщений с пропускной способностью канала – одна из наиболее важных задач кодирования.
Коды бывают первичные (простые или примитивные) и помехоустойчивые. Простые коды состоят из всех кодовых слов, возможных при данном способе кодирования. Превращение одного символа кодового слова в другое из-за действия помех дает новое кодовое слово. Возникает ошибка, которую нельзя обнаружить. В помехоустойчивых кодах применяют лишь часть из общего числа возможных кодовых слов. Применяемые слова называют разрешенными, остальные – запрещенными. Помехоустойчивое кодирование позволяет повысить верность передачи сообщений.
Различают кодирующие устройства (кодеры) для источника информации и для канала связи. Задачей первого является экономное (в смысле минимума среднего числа символов) представление сообщений, а задачей второго – обеспечение достоверной передачи сообщений.
Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Декодирующее устройство (декодер) вместе с кодером образует кодек. Обычно кодек – логическое устройство.
Примитивное (безизбыточное) кодирование применяют для согласования алфавита источника с алфавитом канала. Тогда избыточность источников (см. п. 2.1), образованных выходом и входом кодера, одинакова. Это кодирование применяют также для шифрования передаваемой информации и повышения устойчивости работы системы синхронизации. В последнем случае правило кодирования выбирают так, чтобы вероятность появления на выходе кодера длинной последовательности, состоящей только из 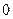 или только из
или только из 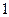 , была минимальна. Подобный кодер называют скремблером (от английского слова ²scramble² - перемешивать).
, была минимальна. Подобный кодер называют скремблером (от английского слова ²scramble² - перемешивать).
Восстановление переданного сообщения в приемнике - всегда приближенное. Часть информации, необходимая для обеспечения требуемой точности восстановления, называется существенной. Сжатие (компрессирование) сообщения (данных) - полное или частичное удаление из него (них) избыточной информации. Решение этой задачи достигается экономным кодированием. Сжатие данных дает экономию памяти запоминающих устройств и пропускной способности каналов. При экономном кодировании избыточность источника, образованного выходом кодера, меньше, чем на входе кодера. Экономное кодирование применяется в ЭВМ. Операционные системы содержат в своем составе программы сжатия данных (динамические компрессоры и архиваторы). Так, стандарт 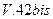 на модемы для связи между ЭВМ по телефонным сетям общего пользования включает сжатие в число процедур обработки данных (см. Приложение).
на модемы для связи между ЭВМ по телефонным сетям общего пользования включает сжатие в число процедур обработки данных (см. Приложение).
Помехоустойчивое (избыточное) кодирование применяют для обнаружения и исправления ошибок, возникающих при передаче сообщения по каналу. Тогда избыточность источника, образованного выходом кодера, больше избыточности источника на входе кодера. Это кодирование распространено в разных системах связи, при хранении и передаче данных в сетях ЭВМ, в цифровой аудио- и видеотехнике.
Число разрядов в различных кодовых словах кода может быть одинаковым или разным. Соответственно, различают равномерные и неравномерные коды. Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми словами. Число разрядов 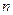 в любом кодовом слове равномерного кода - разрядность кода. Для равномерного кода число возможных комбинаций
в любом кодовом слове равномерного кода - разрядность кода. Для равномерного кода число возможных комбинаций 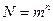 .
.
Пример 1.2.1. Примитивным равномерным кодом, используемым в телеграфии, является код Бодо с 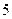 двоичными элементами в каждом слове (
двоичными элементами в каждом слове (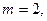
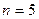 ). Полное число слов
). Полное число слов 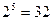 . Этого достаточно для кодирования
. Этого достаточно для кодирования 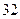 букв русского алфавита, но недостаточно для передачи сообщения, содержащего буквы, цифры и разные условные знаки (точка, запятая, сложение, умножение и т.п.). Тогда можно применить ²Международный код №2² (МТК-2) с регистровым принципом. В нем одно и то же
букв русского алфавита, но недостаточно для передачи сообщения, содержащего буквы, цифры и разные условные знаки (точка, запятая, сложение, умножение и т.п.). Тогда можно применить ²Международный код №2² (МТК-2) с регистровым принципом. В нем одно и то же 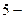 элементное кодовое слово можно использовать до трех раз в зависимости от положения регистра: русский, латинский и цифровой. Общее число разных знаков равно
элементное кодовое слово можно использовать до трех раз в зависимости от положения регистра: русский, латинский и цифровой. Общее число разных знаков равно 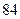 , что достаточно для кодирования телеграммы. Для передачи данных рекомендован
, что достаточно для кодирования телеграммы. Для передачи данных рекомендован 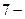 элементный код МТК-5
элементный код МТК-5 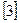 .
.
В неравномерных кодах кодовые слова различаются не только расположением символов, но и их числом. Эти коды требуют либо специальных разделительных знаков, указывающих конец одного и начало другого кодового слова, либо строятся так, чтобы никакое кодовое слово не было началом другого. Префиксные (неприводимые) коды удовлетворяют последнему условию. Заметим, что равномерный код является неприводимым.
Строение кода удобно представить в виде графа (кодового дерева), в котором из каждого узла исходит число ветвей, равное основанию кода (для двоичного кода, например, шаг вверх означает 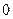 , шаг вниз -
, шаг вниз - 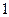 ).
).
Пример 1.2.2. Код Морзе - типичный пример неравномерного двоичного кода 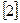 . В нем символы
. В нем символы 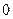 и
и 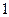 применяются лишь в двух сочетаниях – как одиночные (
применяются лишь в двух сочетаниях – как одиночные (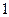 и
и 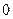 ) или как тройные (
) или как тройные (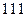 и
и 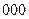 ). Сигнал, соответствующий
). Сигнал, соответствующий 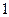 , называется точкой, а
, называется точкой, а 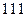 – тире. Символ
– тире. Символ 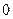 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность
используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 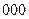 применяется как знак разделения кодовых слов.
применяется как знак разделения кодовых слов.
Простой алгоритм получения неравномерных префиксных кодов предложили Шеннон и Фано. Алгоритм Шеннона-Фано для двоичного кода – следующий. Символы алфавита источника записывают в порядке без увеличения вероятностей их появления. Затем символы разделяют на 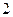 части так, чтобы суммы вероятностей символов в каждой из этих частей были примерно одинаковы. Всем символам
части так, чтобы суммы вероятностей символов в каждой из этих частей были примерно одинаковы. Всем символам 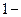 ой (
ой (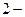 ой) части приписывают
ой) части приписывают 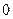 (
(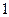 ) в качестве
) в качестве 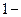 ого символа слова кода. Каждую из
ого символа слова кода. Каждую из 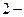 х частей (если в ней больше
х частей (если в ней больше 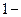 го символа) делят еще на две, по возможности, равновероятные части. К ним применяют то же правило кодирования. Процесс повторяют, пока в каждой из полученных частей не останется по
го символа) делят еще на две, по возможности, равновероятные части. К ним применяют то же правило кодирования. Процесс повторяют, пока в каждой из полученных частей не останется по 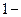 му символу. Деление на части с ²примерно равными вероятностями² - не всегда однозначная процедура. Погрешности кодирования можно уменьшить, а код сделать более эффективным, перейдя от посимвольного кодирования к кодированию последовательностей символов сообщения методом укрупнения алфавита (см. п. 4.2).
му символу. Деление на части с ²примерно равными вероятностями² - не всегда однозначная процедура. Погрешности кодирования можно уменьшить, а код сделать более эффективным, перейдя от посимвольного кодирования к кодированию последовательностей символов сообщения методом укрупнения алфавита (см. п. 4.2).
Пример 1.2.3. Пусть алфавит 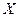 источника состоит из символов
источника состоит из символов 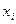 ,
, 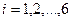 . Вероятности появления символов на выходе источника, соответственно, равны
. Вероятности появления символов на выходе источника, соответственно, равны  ,
, 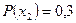 ,
, 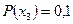 ,
, 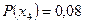 ,
, 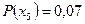 и
и 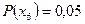 . Процедура Шеннона-Фано построения неравномерного кода без укрупнения алфавита источника задается табл. 1.1
. Процедура Шеннона-Фано построения неравномерного кода без укрупнения алфавита источника задается табл. 1.1 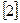 .
.
Таблица 1.1. Кодирование источника по методу Шеннона-Фано
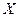
|
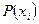
| Выбор символов неравномерного кода |
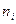
| |||
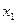
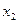

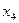
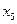

| 0,4 0,3 0,1 0,08 0,07 0,05 |
На 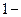 ом этапе множество символов делим на
ом этапе множество символов делим на 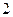 части:
части: 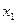 и
и 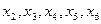 ; на
; на 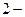 ом -
ом - 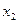 и
и 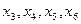 ; на
; на 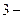 ем -
ем - 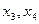 и
и 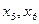 ; на
; на 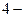 ом -
ом -  и
и 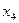 ,
, 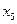 и
и  . Более вероятным символам источника присвоим кодовые слова меньшей длины
. Более вероятным символам источника присвоим кодовые слова меньшей длины 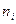 . Построили префиксный код. Средняя длина кодового слова (среднее число символов кода на один символ источника)
. Построили префиксный код. Средняя длина кодового слова (среднее число символов кода на один символ источника) 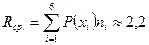 .
.
Помехоустойчивые коды бывают блоковые и непрерывные. При блоковом кодировании последовательность символов источника разбивают на отрезки. Каждому отрезку соответствует определенная последовательность (блок) кодовых символов - кодовое слово. Множество кодовых слов, возможных при данном способе кодирования, образует блоковый код. В равномерном (неравномерном) коде длина блока - постоянная (переменная). Помехоустойчивые коды - обычно равномерные.
Блоковые коды бывают разделимые и неразделимые. В разделимом коде 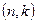 длины
длины 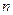 символы можно разделить по назначению на
символы можно разделить по назначению на 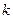 информационных (несущих информацию о сообщении) и
информационных (несущих информацию о сообщении) и 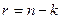 проверочных. Скорость кода
проверочных. Скорость кода 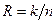 . Полное число слов в коде равно
. Полное число слов в коде равно 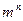 , а
, а 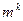 - число разрешенных слов. В неразделимых кодах нельзя выделить информационные и проверочные символы. Например, - это коды с постоянным весом и коды на основе матриц Адамара (см. п. 6.3). В двоичном коде с постоянным весом кодовые слова содержат одинаковое число
- число разрешенных слов. В неразделимых кодах нельзя выделить информационные и проверочные символы. Например, - это коды с постоянным весом и коды на основе матриц Адамара (см. п. 6.3). В двоичном коде с постоянным весом кодовые слова содержат одинаковое число 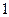 . В стандартном телеграфном коде № 3 любое из них содержит три
. В стандартном телеграфном коде № 3 любое из них содержит три 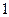 и четыре
и четыре 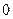
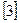 .
.
Разделимые коды бывают линейные и нелинейные. В линейных кодах сумма по 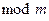 (см. (1.1))
(см. (1.1)) 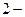 х любых кодовых слов образует кодовое слово того же кода. Линейный код называется систематическим, если первые
х любых кодовых слов образует кодовое слово того же кода. Линейный код называется систематическим, если первые 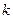 символов любого его кодового слова являются информационными, а остальные
символов любого его кодового слова являются информационными, а остальные 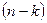 - проверочными. Подкласс линейных кодов - циклические коды (см. п. 6.5). В них все наборы, образованные циклической перестановкой символов в любом кодовом слове, являются кодовыми словами того же кода. Это свойство упрощает построение кодека, особенно – при обнаружении и исправлении одиночных ошибок. Примеры циклических кодов - коды Хэмминга, коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) и другие. Пример нелинейного двоичного кода - код Бергера (см. п. 1.4). В нем проверочные символы образованы двоичной записью числа
- проверочными. Подкласс линейных кодов - циклические коды (см. п. 6.5). В них все наборы, образованные циклической перестановкой символов в любом кодовом слове, являются кодовыми словами того же кода. Это свойство упрощает построение кодека, особенно – при обнаружении и исправлении одиночных ошибок. Примеры циклических кодов - коды Хэмминга, коды Боуза-Чоудхури-Хоквингема (БЧХ-коды) и другие. Пример нелинейного двоичного кода - код Бергера (см. п. 1.4). В нем проверочные символы образованы двоичной записью числа 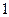 в последовательности информационных символов.
в последовательности информационных символов.
Непрерывное кодирование и декодирование делают над непрерывной последовательностью символов без разбиения ее на блоки. Среди непрерывных наиболее часто применяют сверточные коды (см. п. 6.8).
Различают каналы связи с независимыми и группирующимися ошибками. Соответственно, помехоустойчивые коды можно разбить на 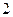 класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Для исправления последних есть много эффективных кодов. На практике целесообразнее применять коды, исправляющие независимые ошибки, вместе с устройством перемежения символов (декорреляции ошибок). Тогда символы кодового слова не передаются последовательно, а перемешиваются с символами других кодовых слов. Если интервал между символами каждого кодового слова сделать больше ²памяти² канала, ошибки в пределах одного слова станут независимыми. Это и позволяет применять коды, исправляющие независимые ошибки.
класса: исправляющие независимые ошибки и исправляющие пакеты ошибок. Для исправления последних есть много эффективных кодов. На практике целесообразнее применять коды, исправляющие независимые ошибки, вместе с устройством перемежения символов (декорреляции ошибок). Тогда символы кодового слова не передаются последовательно, а перемешиваются с символами других кодовых слов. Если интервал между символами каждого кодового слова сделать больше ²памяти² канала, ошибки в пределах одного слова станут независимыми. Это и позволяет применять коды, исправляющие независимые ошибки.
В Приложении проиллюстрированы принципы построения кодов и сжатия данных на примере компьютерных сетей.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 2639; Нарушение авторских прав?; Мы поможем в написании вашей работы!