
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обнаружение и исправление ошибок корректирующими кодами
|
|
|
|
Декодирование сообщения в приемнике – это не просто операция, обратная кодированию сообщения в передатчике. Из-за разных искажений и воздействия помех пришедший сигнал может существенно отличаться от переданного. Можно высказать ряд предположений о том, какое сообщение передавалось. Задачей приемного устройства является принятие решения о том, какое из возможных сообщений действительно передавалось источником. Принятие решения о принятом слове, вообще говоря, предполагает анализ всех сведений об источнике и канале связи. Из-за введения избыточности помехоустойчивый код может обнаружить и исправить ошибки в принятых словах. Это способствует повышению достоверности передачи информации. При передаче сообщений ошибки возникают из-за действия помех и обнаруживаются при приеме запрещенных слов приемником. Долю обнаруживаемых ошибок оценим как 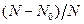 , где
, где 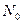 (
(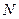 ) - число разрешенных слов (их полное число) в коде. Избыточность корректирующего кода
) - число разрешенных слов (их полное число) в коде. Избыточность корректирующего кода
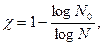 . (1.3)
. (1.3)
где для простого кода 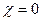 , так как
, так как 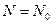 .
.
Множество запрещенных кодовых слов числом  разобьем на
разобьем на 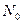 подмножеств
подмножеств  , где
, где 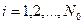 . Каждому подмножеству
. Каждому подмножеству  сопоставим разрешенное кодовое слово
сопоставим разрешенное кодовое слово 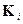 . Зададим правило приема. Если принято кодовое слово
. Зададим правило приема. Если принято кодовое слово 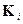 или любое слово из подмножества
или любое слово из подмножества  , то считаем, что было передано кодовое слово
, то считаем, что было передано кодовое слово 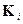 . Тогда исправляются все ошибки, не выводящие передаваемое кодовое слово за пределы подмножества
. Тогда исправляются все ошибки, не выводящие передаваемое кодовое слово за пределы подмножества  . В подмножество
. В подмножество  входят запрещенные слова
входят запрещенные слова 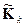 , при приеме которых наиболее вероятна передача слова
, при приеме которых наиболее вероятна передача слова 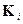 , то есть удовлетворяющие условию
, то есть удовлетворяющие условию
 (1.4)
(1.4)
где 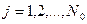 ,
, 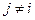 ,
, 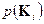 (
(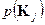 ) - априорная вероятность передачи кодового слова
) - априорная вероятность передачи кодового слова 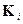 (
(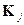 ),
), 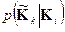 (
(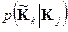 ) - переходная вероятность приема кодового слова
) - переходная вероятность приема кодового слова 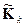 при условии передачи слова
при условии передачи слова 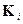 (
(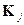 ).
).
Вектор ошибок 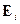 определяет различие между принятым словом
определяет различие между принятым словом 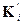 и переданным
и переданным 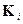 :
:
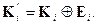 (1.5)
(1.5)

Если нет ошибок при передаче двоичного кодового слова 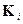 , принятое кодовое слово
, принятое кодовое слово 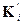 совпадает с
совпадает с 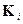 , и вектор ошибок
, и вектор ошибок 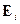 во всех разрядах содержит
во всех разрядах содержит 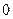 . Число ненулевых символов в векторе ошибок дает его вес
. Число ненулевых символов в векторе ошибок дает его вес 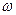 .
.
Рассмотрим канал с независимо возникающими ошибками. Пусть вероятности 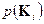 передачи разных сообщений
передачи разных сообщений 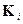 из их ансамбля
из их ансамбля 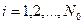 одинаковы. Тогда вероятность появления ошибки уменьшается с увеличением кратности ошибки. В первую очередь надо исправлять однократные ошибки – они встречаются наиболее часто, затем – двукратные и т.д.
одинаковы. Тогда вероятность появления ошибки уменьшается с увеличением кратности ошибки. В первую очередь надо исправлять однократные ошибки – они встречаются наиболее часто, затем – двукратные и т.д.
Пусть в каждое из подмножеств  включены запрещенные слова
включены запрещенные слова 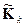 , отличные от соответствующего разрешенного слова
, отличные от соответствующего разрешенного слова 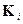 в меньшем числе символов, чем от других разрешенных слов
в меньшем числе символов, чем от других разрешенных слов 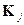 ,
, 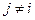 . Такой подход к формированию подмножеств
. Такой подход к формированию подмножеств  соответствует декодеру, принимающему решение о каждом переданном символе на основании принятого символа, оптимальное по критерию максимума правдоподобия.
соответствует декодеру, принимающему решение о каждом переданном символе на основании принятого символа, оптимальное по критерию максимума правдоподобия.
Пример 1.4.1. В симметричном стационарном двоичном канале без памяти ошибки независимы друг от друга, так как между ними нет статистических связей. Кроме того, алфавиты на входе и выходе канала содержат одинаковое число символов. Вероятность ошибки 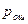 при передаче любого символа одинакова и не меняется во времени.
при передаче любого символа одинакова и не меняется во времени.
Пример 1.4.2. Пусть число 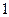 , перешедших в
, перешедших в 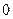 в каждом кодовом слове из-за действия помех, не равно числу
в каждом кодовом слове из-за действия помех, не равно числу 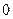 , перешедших в
, перешедших в 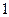 . Тогда двоичные коды с постоянным весом
. Тогда двоичные коды с постоянным весом 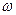 обнаруживают все ошибки кратности
обнаруживают все ошибки кратности 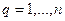 . В полностью асимметричном канале связи возможен лишь один вид ошибок - преобразование
. В полностью асимметричном канале связи возможен лишь один вид ошибок - преобразование 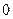 в
в 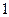 или
или 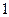 в
в 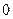 . В нем такой код находит все ошибки. В симметричном канале с вероятностью искажения символа
. В нем такой код находит все ошибки. В симметричном канале с вероятностью искажения символа 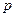 вероятность пропуска ошибки
вероятность пропуска ошибки 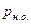 в первом приближении определяется как вероятность одновременного искажения одной
в первом приближении определяется как вероятность одновременного искажения одной 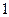 и одного
и одного 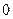 . Для телеграфного кода № 3
. Для телеграфного кода № 3 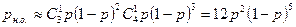 , где
, где 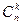 - число сочетаний из
- число сочетаний из 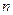 элементов по
элементов по 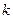 ,
, 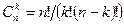 .
.
Пример 1.4.3. Каждое кодовое слово наиболее простого из линейных систематических двоичных кодов 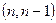 содержит
содержит 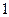 проверочный символ, равный сумме по
проверочный символ, равный сумме по 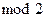 всех информационных символов. Это - код с проверкой на четность. Для него кодовое расстояние
всех информационных символов. Это - код с проверкой на четность. Для него кодовое расстояние 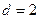 , что позволяет гарантированно обнаружить лишь однократные ошибки. Слова такого кода имеют только четные веса. Вероятность пропуска ошибки в
, что позволяет гарантированно обнаружить лишь однократные ошибки. Слова такого кода имеют только четные веса. Вероятность пропуска ошибки в 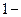 ом приближении равна вероятности искажения
ом приближении равна вероятности искажения 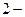 х символов:
х символов: 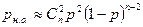 .
.
Есть видоизмененный способ контроля на четность. Последовательность информационных символов 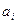 , где
, где 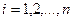 , разбивается на
, разбивается на 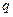 строк по
строк по 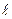 символов в каждой так, что
символов в каждой так, что 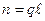 . Контрольные разряды
. Контрольные разряды 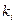 , где
, где 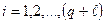 , выделены каждой строке и каждому столбцу по следующей схеме:
, выделены каждой строке и каждому столбцу по следующей схеме:
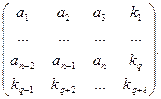
Контроль на четность делается по строкам и по столбцам. Если, например, нарушение четности обнаружено для 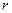 -ой строки и
-ой строки и 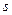 -ого столбца, то символ
-ого столбца, то символ 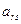 матрицы - ошибочный. Исправление обнаруженной ошибки достигается заменой этого символа (
матрицы - ошибочный. Исправление обнаруженной ошибки достигается заменой этого символа (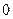 - на
- на 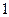 или
или 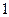 - на
- на 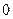 ).
).
Контроль по методу четности (или нечетности) применяют при записи-считывании информации в запоминающих устройствах и при выполнении арифметических операций на ЭВМ (см. Приложение).
Пример 1.4.4. Нелинейные коды Бергера, например, - 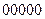 ,
, 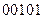 ,
, 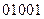 ,
, 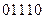 ,
, 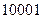 ,
, 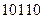 ,
,  ,
, 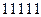 , применяются, как правило, в асимметричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных.
, применяются, как правило, в асимметричных каналах. В симметричных каналах они обнаруживают все одиночные ошибки и некоторую часть многократных.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 394; Нарушение авторских прав?; Мы поможем в написании вашей работы!