И контекстно-свободных языков

Форме

Обобщенные КС-грамматики и приведение их к удлиняющей

КС-грамматика называется обобщенной, если она содержит аннулирующие правила (e - правила), то есть правила вида A® e, где e - пустая цепочка. Обобщенная грамматика зачастую более проста и наглядна. Тем не менее следует помнить, что для любой обобщенной КС-грамматики существует эквивалентная неукорачивающая КС-грамматика.

Теорема 4.6. Каждая КС-грамматика приводима к виду с не более чем одним аннулирующим правилом S® e, которого может и не быть.

Доказательство. Проведем его, как обычно, конструктивно, построением неукорачивающей грамматики.

Во-первых, нужно определить, порождает ли исходная грамматика пустую цепочку. Пусть S - начальный символ исходной грамматики G. Определим в G множество нетерминалов X _i, из которых пустую цепочку можно получить за i шагов, и множество новых нетерминалов Z_i. Таким образом, мы определим аннулирующие нетерминалы.

X₀ = { A | $ A® e }, Z₀ = X₀

X₁ = { A | $ A® x, где xÎ X₀ }, Z₁ = X₁\ X₀

....................................................................

X _i = { A | $ A® x, где xÎ 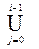X _j }, Z _i = X _i\ X _i-1

На каком-то шаге Z _i станет равным Æ и процесс формирования аннулирующих нетерминалов можно закончить. Если S Ï X _j, где 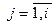, то e Ï L(G) и правила S® e добавлять не надо. В противном случае, заменим в исходной грамматике во всех правилах S на S₁, введем новый исходный нетерминал S и к правилам грамматики G добавим правила

S® e ½ S₁.

Все остальные правила вида A® e можно удалить. Для этого заменим каждое из правил, правые части которых содержат хотя бы по одному аннулирующему нетерминалу, множеством новых правил. Если правая часть правила содержит k вхождений аннулирующих нетерминалов, то множество, заменяющее это правило, будет состоять из 2^k правил, соответствующих всем возможным способам удаления некоторых (или всех) из этих вхождений.

Пусть имеется правило

B® j ₁ A ₁ j ₂ A ₂ j ₃ ... j _k A _k j _k+1,

где A _i () - аннулирующие нетерминалы. Добавим к этому правилу следующие правила:

B® j ₁ j ₂ A ₂ j ₃ ... j _k A _k j _k+1, удалено A ₁

B® j ₁ A ₁ j ₂ j ₃ ... j _k A _k j _k+1, удалено A ₂

..................................

B® j ₁ A ₁ j ₂ A ₂ j ₃ ... j _k j _k+1, удалено A _k

B® j ₁ j ₂ j ₃ ... j _k A _k j _k+1, удалены A ₁, A ₂

..................................

B® j ₁ j ₂ j ₃ ... j _k j _k+1, удалены A ₁, A ₂,... A _k

Заметим, что в случае неоднозначности на этом шаге может получиться меньше чем 2^k правил. Так, для аннулирующего нетерминала A правило

B® aAA будет заменяться тремя правилами B® aAA ½ aA ½ a, так как в данном случае безразлично первое или второе вхождение A мы рассматриваем.

После такой замены правил для всех правых частей исходной грамматики, содержащих аннулирующие нетерминалы, исключим из грамматики все e - правила, включая те, которые могли появиться при замене.

В результате мы получим грамматику, эквивалентную исходной, что доказывается с использованием теорем 4.1 и 4.3.

Отметим, что мы рассматривали случай, когда аннулирующие нетерминалы имеют и другие альтернативы, кроме перехода в пустую цепочку. Если A ® e единственная альтернатива нетерминала A, то правые части правил, содержащие его вхождение, можно просто исключить. ƒ

В результате применения рассмотренного алгоритма можно получить КС-грамматику, по которой вывод любой непустой цепочки характеризуется тем, что сентенциальная форма, получаемая на каждом шаге вывода, будет не короче предыдущей. Не случайно полученная грамматика носит название неукорачивающей КС-грамматики (НКС-грамматики).

Пример 4.5. Рассмотрим обобщенную КС-грамматику с аксиомой <число>

<число> ® <знак> <цел.часть>. <др.часть>

<знак> ® + ½ - ½ e

<цел.часть> ® <цел.часть><цифра> ½ e

<др.часть> ® <цел.часть>

<цифра> ® 0 ½ 1 ½...½ 8 ½ 9

и приведем ее к неукорачивающей форме.

Вначале покажем, что данная грамматика не порождает пустой цепочки. Здесь

X₀ = { <знак>, <цел.часть> },

X₁ = { <др.часть> },

X₂ = Æ и Z₂ = Æ.

Среди множеств X - нет нетерминала <число> и, следовательно, правила

<число> ® e

добавлять не надо.

Проведем замены правил, правые части которых содержат аннулирующие нетерминалы, а затем удалим e - правила.

В результате получим грамматику

<число> ® <знак> <цел.часть>. <др.часть> ½ <цел.часть>. <др.часть> ½

<знак>. <др.часть> ½ <знак> <цел.часть>. ½. <др.часть> ½

<цел.часть>. ½ <знак>. ½.

<цел.часть> ® <цел.часть><цифра> ½ <цифра>

<др.часть> ® <цел.часть>

<цифра> ® 0 ½ 1 ½...½ 8 ½ 9

На рис. 4.2 представлены деревья вывода цепочки +.9 по исходной (рис. 4.2 (а)) и результирующей (рис. 4.2 (б)) грамматикам.

š

Для приведения грамматики к удлиняющей форме необходимо кроме аннулирующих правил исключить и цепные правила. Цепное правило - это правило вида A® B, где A, B Î N.

Теорема 4.7. Для любой КС-грамматики существует эквивалентная ей грамматика без цепных правил.

Доказательство. Пусть в грамматике имеется правило A ® B и A ¹ S (A - не начальный символ грамматики). Тогда все правила вида C ® aAb заменим на правила C ® aBb, а правила A ® B удалим. Если A = S и для B существуют правила B ® j ₁ ½ ... ½ j _n, то заменим их на S ® j ₁ ½ ... ½ j _n , после чего S ® B удалим.

Любое такое преобразование правил допустимо исходя из теорем 4.1 - 4.3 и устраняет правила вида A ® B. Повторяем такие преобразования до тех пор, пока в грамматике не останется цепных правил. š

В результате устранения аннулирующих и цепных правил получается грамматика в удлиняющей форме, где сентенциальная форма на каждом шаге вывода будет длиннее сентенциальной формы на предыдущем шаге. Напомним, что эта форма грамматики использовалась для доказательства теоремы о разрешимости контекстных языков (теорема 1.1).

Пример 4.6. Пусть дана КС-грамматика с правилами

S ® aBa

B ® A ½ Bc

A ® aA ½ bb.

Правило B ® A можно устранить, воспользовавшись результатами теоремы 4.2, и получить грамматику

S ® aBa

B ® aA ½ bb ½ Bc

A ® aA ½ bb š

КС-грамматика G=(N,S,P,S) называется грамматикой без циклов, если в ней нет выводов A Þ⁺ A для AÎ N. КС-грамматика G называется приведенной, если она без циклов, без аннулирующих правил и без тупиков.

Грамматики с e - правилами и циклами иногда труднее анализировать, чем грамматики без таковых. Кроме того, в любой практической ситуации тупики (бесполезные символы) без необходимости увеличивают объем анализатора. Поэтому для некоторых алгоритмов синтаксического анализа, рассматриваемых во второй части пособия, мы будем требовать, чтобы грамматики, фигурирующие в них, были приведенными. Это требование позволяет рассматривать все КС-языки.

Теорема 4.8. Если L - КС-язык, то L=L(G) для некоторой приведенной КС-грамматики G.

Доказательство. Применить к КС-грамматике, определяющей язык L, эквивалентные преобразования по теоремам 4.5 - 4.7.?

4.4. Устранение левой рекурсии и левая факторизация

В целом ряде приложений требуется, чтобы грамматика рассматриваемого языка не содержала левой рекурсии. Наличие леворекурсивных правил в исходной грамматике не фатально, так как для любой КС-грамматики существует эквивалентная грамматика без левой рекурсии.

Рассмотрим случай когда правила грамматики саморекурсивны, то есть левая часть правила и край правой части совпадают. Пусть нетерминал A имеет m леворекурсивных правил

A ® Aa _i для 1 £ i £ m

и n правил

A ® b _j для 1 £ j £ n,

которые не являются леворекурсивными (отметим, что отсутствие последних делает A тупиком).

Заменив эти правила на правила

A ® b_j <список A> для 1 £ j £ n

<список A> ® a _i <список A> для 1 £ i £ m

<список A> ® e,

где <список A> - новый нетерминал, мы получим эквивалентную группу правил без левой рекурсии.

Пример 4.7. Самой короткой грамматикой для представления идентификатора является леворекурсивная грамматика

<И> ® б ½ <И>б ½ <И>ц,

где б - любая буква, а ц - любая цифра. В данной грамматике два леворекурсивных правила и одно правило без левой рекурсии. Заменяя их на правила

<И> ® б<И₁>

<И₁> ® б<И₁> ½ ц<И₁> ½ e,

мы получим обобщенную праворекурсивную грамматику идентификатора. Заметим, что исключение аннулирующего правила приведет нас к грамматике из примера 4.3. š

Если в грамматике имеется группа правил вида

A ® ab ₁ ½ ... ½ ab _n,

то цепочку a можно “вынести за скобку” и преобразовать данную группу правил к виду

A ® a B

B ® b ₁ ½ ... ½ b _n.

Этот прием носит название левой факторизации и его необходимо знать для ряда приложений.

Упражнения

4.1. В грамматике

S ® abAcDkY

A ® nmDky ½ vaxYe ½ jab

D ® ghYo ½ kh

Y ® f ½ d

устраните правила

A ® nmDky ½ vaxYe ½ jab

D ® ghYo ½ kh

и проведите декомпозицию относительно Y. Подсчитайте количество правил результирующей грамматики и грамматики до проведения преобразований.

4.2. Исключите тупики из следующих грамматик:

(а)

S ® aBcD ½ kLMp L ® f M

B ® cLpDq ½ pDc ½ f M ® Lk ½ pMLc

D ® f Dr ½ f pq K ® r F

F ® abc ½ ab

(б)

S ® AB ½ BC ½ kL A ® aA ½ bL ½ c

B ® BS ½ AL L ® cB ½ j ½ p

C ® QS ½ dC Q ® qQ ½ aC

M ® xN ½ yM ½ zS ½ h N ® xC ½ v ½ wM

(в)

S ® BA ½ CB ½ AL C ® QS ½ dC

A ® aA ½ bB ½ cC Q ® qQ ½ aC

B ® BS ½ AL ½ g M ® xN ½ yM ½ zS ½ h

L ® cB ½ jC ½ p N ® xC ½ v ½ wM

4.3. Устраните аннулирующие правила из следующих грамматик:

(а)

S ® abCDe ½ Kp

C ® dSde ½ e

D ® dD ½ DD ½ e ½ f K ½ e

K ® e ½ mcf

(б)

S ® aSbS ½ bSaS ½ e

(в)

S ® ABC A ® BB ½ e

B ® CC ½ a C ® AA ½ b

4.4. Устраните цепные правила из грамматики

E ® E+T ½ T

T ® T * F ½ F

F ® (E) ½ a

4.5. Найдите приведенную грамматику, эквивалентную грамматике

S ® A ½ B A ® C ½ D

B ® D ½ E C ® S ½ a ½ e

D ® S ½ b E ® S ½ c ½ e

4.6. Устраните левую рекурсию в следующих грамматиках:

(а)

E ® E+T ½ E-T ½ T ½ -T

T ® T * F ½ T / F ½ F

F ® (E) ½ a

(б)

S ® AB

A ® Aa ½ Ab ½ d ½ e

B ® qK ½ rB ½ Bf ½ Bg

K ® vS ½ w

Глава 5. СВОЙСТВА АВТОМАТНЫХ

5.1. Общий вид цепочек А-языков и КС-языков.

5.2. Операции над языками.

5.2.1. Операции над КС-языками.

5.2.2. Операции над А-языками.

5.2.3. Операции над К-языками.

5.3. Выводы для практики.

5.4. Неоднозначность КС-грамматик и языков.

Упражнения

В этой главе мы исследуем некоторые из основных свойств А- и КС-языков. Упомянутые здесь результаты образуют малую долю огромного богатства знаний об этих языках. Часть свойств этих языков уже были рассмотрены в главах 1-4. Ниже мы обсудим общий вид цепочек этих языков, неоднозначность КС-грамматик и КС-языков, некоторые операции, относительно которых замкнуты классы А- и КС-языков.

5.1. Общий вид цепочек А-языков и КС-языков

Мы хотим получить характеристику цепочек А-языков, которая будет полезна для доказательства того, что некоторые языки не являются автоматными. Следующую теорему об общем виде цепочек А-языков называют теоремой о “разрастании”, потому что она в сущности говорит о том, что если даны А-язык и достаточно длинная цепочка в нем, то в этой цепочке можно найти непустую подцепочку, которую можно повторить сколько угодно раз (т.е. она “разрастается”), и все полученные таким образом “новые” цепочки будут принадлежать тому же А-языку. С помощью этой теоремы часто приводят к противоречию предположение о том, что некоторый язык является автоматным.

Теорема 5.1. Пусть L - А-язык. Существует такая константа p, что если y Î L и ½y½³ p, то цепочку y можно записать в виде abg, где 0 <½b½£ p и ab ⁱg Î L, для всех i ³ 0.

Доказательство. Если L - конечный язык, то положим константу p больше длины самой длинной цепочки языка L, тогда ни одна из цепочек языка не удовлетворяет условиям теоремы и она верна. В противном случае, пусть

M = (Q, S, d, q₀, F) - конечный автомат с n состояниями и L(M) = L. Пусть p = n. Если y Î L и ½ y ½ ³ n, рассмотрим последовательность конфигураций, которую проходит автомат M, допуская цепочку y. Так как в этой последовательности, по крайней мере, n+1 конфигурация, то найдутся две конфигурации с одинаковыми состояниями. Поэтому должна быть такая последовательность тактов, что

(q ₀, abg) ú¾^* (q ₁, bg) ú¾ ^k (q ₁, g) ú¾^* (q ₂, e)

для некоторого q ₁ и 0 < k £ n. Отсюда 0 <½b½£ n.

Но тогда для любого i > 0 автомат может проделать следующую последовательность тактов:

(q ₀, ab ⁱ g) ú¾^* (q ₁, b ⁱ g)

(q ₁, b ⁱ g) ú¾ ⁺ (q ₁, b ^i-1 g)

..............

(q ₁, b ² g) ú¾ ⁺ (q ₁, bg)

(q ₁, bg) ú¾ ⁺ (q ₁, g)

(q ₁, g) ú¾^* (q ₂, e).

Для случая i = 0 все еще очевиднее:

(q ₀, ag) ú¾^* (q ₁, g) ú¾^* (q ₂, e).

Так как abg Î L, то и ab ⁱ g Î L, для всех i ³ 0. š

Эта теорема обычно используется для доказательства того, что некоторые выбранные цепочки не являются цепочками А-языка и, следовательно, не могут быть определены А-грамматиками.

Следствие 5.1. Язык L, состоящий из цепочек x ⁿ y ⁿ, не является автоматным языком.

Допустим, что он автоматный. Тогда для достаточно большого n цепочка x ⁿ y ⁿ может быть представлена в виде abg, причем b ¹ e и ab ⁱ g Î L для всех i ³ 0.

Если b = x...x или b = y...y, то ag = ab ⁰ g Ï L, так как количество символов x и y в цепочке ag различно. Если b = x...xy...y, то abbg = ab ²g Ï L, так как в цепочке abbg символы x и y будут перемешаны. Полученное противоречие доказывает, что L - не является А-языком. š

Следствие 5.2. Язык арифметических выражений не является А-языком, так как он может содержать произвольное количество вложенных скобок, причем количество открывающих скобок совпадает с количеством закрывающих. Аналогично не является А-языком любой язык, содержащий вложенные конструкции типа фигурных скобок в языке C, begin - end, repeat - until и т.п. Каждая конечная А-грамматика, порождающая подобные конструкции, будет выводить и цепочки с неравным количеством открывающих и закрывающих скобок. Тем не менее, анализировать подобные цепочки можно и с помощью автоматного подхода. При этом, в синтаксисе языка допускается произвольное количество открывающих и закрывающих скобок, а контроль их парности возлагается на семантические подпрограммы. š

Прежде чем рассматривать теорему о разрастании КС-языков, примем без доказательств следующую теорему.

Теорема 5.2. Для любой КС-грамматики, которая не допускает вывода вида А Þ⁺ aАb,

где ½a½> 0 и ½b½> 0, можно построить эквивалентную А-грамматику. š

Иными словами, любой язык, который при описании КС-грамматикой не содержит самовставляемых нетерминалов, включает только одностороннюю рекурсию, при выводе наращивает цепочку в одну сторону, неважно, влево или вправо, является автоматным языком.

Теорема 5.3. Для любого КС-языка L существует постоянная p такая, что если y Î L и ½y½ > p, то y = abgjl, где b¹e, j¹e и ab ⁱgj ⁱl Î L для любого i³0.

Доказательство. Аналогично с теоремой 5.1 рассмотрим только случай бесконечных языков.

Рассмотрим в бесконечном КС-языке L бесповторные деревья вывода, то есть такие, у которых ни на одной ветви нет повторяющихся нетерминалов. Таких деревьев конечное число. Максимальная высота бесповторного дерева

v - равна количеству нетерминалов грамматики. Если максимальная длина правых частей правил грамматики равна b, то максимальная длина цепочки, выводимой бесповторными деревьями, будет не более b^v. Положим p = b^v. Рассмотрим цепочку с длиной больше p и ту ветвь ее дерева вывода, в которой нетерминалы повторяются.

Рассмотрим поддеревья D₁ и D₂, начинающиеся с повторяющегося нетерминала A. Если D₁ заменить на D₂, то получим дерево вывода цепочки agl. Подвеска дерева D₂ к корню D₁ возможна, так как после нее корень дерева D₁ соответствует применению того же правила, что и корень дерева D₂. Таким образом, полученное дерево вывода является деревом вывода в той же грамматике.

Если D₂ заменить на D₁, то получим дерево вывода цепочки ab ²gj ²l. Дерево D₁, которым заменяется D₂, содержит в себе D₂ в качестве поддерева. Заменив его на D₁, получим дерево вывода цепочки ab ³gj ³l. Продолжая такие замены, можно получить любую из цепочек ab ⁱgj ⁱl. š

Пример 5.1. Пусть дана КС-грамматика с правилами:

S ® aAp

A ® cAc ½ cbAb ½ d.

Максимальная высота бесповторного дерева здесь равна 2, а максимальная длина цепочки, выводимая бесповторным деревом, равна 3 (бесповторно выводится только цепочка adp). На рис. 5.1 (а) показано дерево вывода цепочки acbdbp. Здесь принято следующее: a = a, b = cb, g = d, j = b, l = p. На рис. 5.1 (б) показана замена поддерева D₁ на D₂, а на рис. 5.1 (в) замена D₂ на D₁. †

Теорема 5.3, как и теорема 5.1, чаще всего используется для доказательства того, что некоторые цепочки не принадлежат КС-языкам.

Следствие 5.3. Язык L, состоящий из цепочек x ⁿy ⁿz ⁿ, не является КС-языком.

Действительно, разделяя эту цепочку на пять частей abgjl любым возможным способом, мы увидим, что либо agl Ï L из-за неравного количества символов x, y и z, либо ab ²gj ²l Ï L из-за перемешивания символов внутри цепочки.

Следствие 5.4. Языки программирования в общем случае не являются КС-языками.

Например, в языках программирования каждая конкретная процедура имеет одно и то же число аргументов в каждом месте, где она упоминается. Можно показать, что такой язык не контекстно-свободен, отобразив множество программ с тремя вызовами одной и той же процедуры на не контекстно-свободный язык { 0 ⁿ 10 ⁿ 10 ⁿ | n³0 }.

В этих языках встречаются и другие явления, характерные для не КС-языков. Так язык, требующий описания идентификаторов, длина которых может быть произвольно большой до их использования, не контекстно-свободен. Правил КС-грамматик для описания таких явлений явно недостаточно.

Однако на практике все языки программирования считаются КС-языками. В компиляторах идентификаторы обычно обрабатываются лексическим анализатором и свертываются в лексемы прежде, чем достигают синтаксического анализатора. Контроль за их описанием до использования, так же как и подсчет числа параметров в процедуре и т.п., возлагается на семантические подпрограммы, не входящие в собственно синтаксический анализ. Это позволяет существенно упростить синтаксис языков программирования.

5.2. Операции над языками

По определению язык - это множество цепочек, следовательно, над языками можно выполнять операции, правомерные как для множеств, так и для цепочек (строк символов). Определим некоторые из них.

Язык L называется объединением языков L₁ и L₂ (L= L₁ È L₂), если он содержит все цепочки из L₁ вместе со всеми цепочками из L₂. Формально

L = {a½a Î L₁ или a Î L₂}.

Язык L называется пересечением языков L₁ и L₂ (L= L₁ Ç L₂), если он содержит все цепочки, принадлежащие как L_1, так и L₂. Формально L={a½a Î L₁ и a Î L₂}.

Язык L называется разностью языков L₁ и L₂ (L= L₁ \ L₂), если он содержит все цепочки из L_1, которые не принадлежат L₂. Формально L={a½aÎL₁ и aÏL₂}.

Язык L называется дополнением языка L₁ (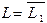), если он содержит все цепочки из некоторого универсального языка L_2, которые не принадлежат L₁. Формально L={a½a Ï L₁}.

Язык L называется конкатенацией (сцеплением) языков L₁ и L₂ (L= L₁ L₂), если он содержит попарные конкатенации всех возможных цепочек из L₁ и L₂. Формально L={ab½a Î L₁ и b Î L₂}.

Итерация языка L, обозначаемая L ^*, определяется следующим образом:

(1) L⁰ = { e },

(2) Lⁿ = LL^n-1 для n ³ 0

(3) L 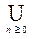^* =Lⁿ.

Позитивная итерация языка L, обозначаемая через L⁺, - это язык 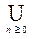Lⁿ. Заметим, что L⁺ = LL ^* = L ^* L и L ^* = L⁺ È { e }.

Язык L называется подстановкой языка L₂ в язык L₁ вместо терминала a (L=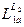), если он содержит все цепочки языка L₁, в которых терминал a заменен на все возможные цепочки языка L₂.

Обращение языка L, обозначаемое L^R, - это язык, содержащий все обращенные цепочки исходного языка. Формально L = {w ^R ½w Î L}.

Прежде чем обсуждать практические аспекты данных определений, поговорим о том, как построить грамматику языка, полученного в результате операций над языками, и как определить ее тип.

5.2.1. Операции над КС-языками

Нетрудно показать, что целый ряд операций над КС-языками дает в результате также КС-язык.

Теорема 5.4. КС-языки замкнуты относительно операций объединения, конкатенации, итерации, подстановки и обращения.

Доказательство. Пусть L₁=L(G₁) и L₂=L(G₂) два контекстно - свободных языка, определяемых КС-грамматиками G₁=( V_T1,V_N1,R₁,S₁ ) и G₂=( V_T2,V_N2,R₂,S₂ ) соответственно. Проиндексируем нетерминалы грамматики G₁ индексом 1, а нетерминалы G₂ - 2, с тем чтобы никакие имена различных грамматик не совпадали.

Если объединить нетерминалы, терминалы, правила исходных грамматик и добавить к последнему объединению правило

S ® S₁ ½ S₂,

где S - аксиома новой результирующей грамматики, то мы, очевидно, получим КС-грамматику, определяющую объединение языков L₁ и L₂. Действительно, индексирование нетерминалов не изменяет класса исходных грамматик, точно так же как и объединение их правил и добавление контекстно-свободной продукции

S ® S₁ ½ S₂.

Последняя продукция и обеспечивает порождение всех цепочек языка L₁ по первой альтернативе правила и всех цепочек языка L₂ по второй его альтернативе.

Таким образом, L= L₁ È L₂ = L(G), где

G=(V_T1 ÈV_T2,V_N1ÈV_N2,R=R₁ÈR₂È{S®S₁|S₂},S ) -

КС-грамматика, определяющая объединение языков L₁ и L₂.

Точно так же можно показать, что КС-грамматика

G=(V_T1 ÈV_T2,V_N1ÈV_N2,R=R₁ÈR₂È{S®S₁S₂},S )

определяет конкатенацию языков L₁ и L₂ (L(G)= L₁ L₂).

Если к правилам P₁ исходной грамматики G₁ добавить правило

S ® SS₁ ½ e,

считая S начальным символом новой КС-грамматики G, то грамматика G будет определять итерацию языка L₁ - L₁ ^*. Если же к R₁ добавить правило

S ® SS₁ ½ S₁ или правило S ® S₁S ½ S₁, или правило S ® SS ½ S₁,

то полученная КС-грамматика G будет определять позитивную итерацию L₁ ⁺.

Если во всех правилах грамматики G₁ вида A ® j ay заменить терминал a на S₂ - аксиому грамматики G₂, то полученная в результате таких преобразований КС-грамматика G будет определять не что иное, как язык L - подстановку языка L₂ в язык L₁ вместо терминала a: , при этом

G=<(V_T1 \{a})ÈV_T2,V_N1ÈV_N2,R=R₁ÈR₂È{S®aS₂b}\{S₁®a a b },S>.

Для того чтобы получить грамматику, определяющую обращение L^R для исходного языка L(G), достаточно обратить левые и правые части правил исходной грамматики G, то есть правила a ® b заменить на правила a ^R ® b ^R (в КС-грамматиках правила A ® b заменяются на правила A ® b ^R). Такие преобразования не изменяют класса КС-грамматик. †

Все рассмотренные преобразования КС-грамматик достаточно очевидны. Рассмотрим на примере только формирование грамматики для обращения языка.

Пример 5.2. Пусть задана грамматика с правилами

S ® aS ½ bB

B ® cB ½ d

Для простоты здесь взята А-грамматика, но ничто не мешает рассматривать ее как КС-грамматику. Цепочки, порождаемые данной грамматикой, состоят из необязательных символов “ а ” в начале цепочки, символа “ b ”, затем необязательных символов “ c ” и символа “ d ” в конце, т.е. цепочка имеет вид

[aaa...]b[ccc...]d,

где квадратные скобки традиционно обозначают необязательный элемент.

Обратим правила заданной грамматики и в результате получим:

S ® Sa ½ Bb

B ® Bc ½ d

Если правила исходной грамматики обеспечивали вывод цепочки слева направо, то полученные правила выводят ее справа налево. Цепочка, порождаемая последней грамматикой, имеет вид d[ccc...]b[aaa...]. †

Теорема 5.5. КС-языки не замкнуты относительно операций пересечения, дополнения и разности.

Доказательство. Языки L₁={a ⁿ b ⁿ c ^j ½ n ³ 1, j ³ 1} и L₂={a ^j b ⁿc ⁿ ½ n ³ 1, j ³ 1} - КС-языки. Первый из них можно определить правилами

S ® XY

X ® aXb ½ ab

Y ® cY ½ c,

а второй

S ® XY

X ® aX ½ a

Y ® bYc ½ bc.

Однако L₁Ç L₂= {aⁿbⁿcⁿ½n ³ 1} - не КС-язык (см. следствие теоремы 5.3). Таким образом, класс КС-языков не замкнут относительно пересечения.

Отсюда можно также заключить, что класс КС-языков не замкнут относительно дополнения. В силу закона де Моргана () любой класс языков, замкнутый относительно объединения и дополнения, должен быть замкнут относительно пересечения. Из теоремы 5.4 известно, что КС-языки замкнуты относительно объединения и предположение об их замкнутости относительно дополнения приводит нас к противоречию с первым доказанным положением данной теоремы.

Для доказательства последнего положения достаточно вспомнить, что дополнение - это, по сути дела, разность множеств. †

5.2.2. Операции над А-языками

Теорема 5.6. Автоматные языки замкнуты относительно операций объединения, конкатенации, итерации, обращения, подстановки, пересечения, дополнения и разности.

Доказательство. Проведем его конструктивно, так же как и в теореме 5.4. Для представления А-грамматик используем графы состояний и в случае операций над двумя языками индексируем нетерминалы исходных грамматик.

Объединение. Пусть даны два А-языка L₁=L(G₁) и L₂=L(G₂) и графы состояний грамматик G₁ и G₂ схематично представлены на рисунках 5.2 (а) и (б), соответственно.

На рис. 5.2 (в) представлена грамматика G, определяющая объединение исходных языков. Для ее построения вводим новый начальный символ S. Если в исходных грамматиках из S _i в A _i ведет ребро, помеченное терминалом a, то проведем ребро из S в A _i и пометим его тем же терминалом a. Выберем новый конечный символ F и все ребра, шедшие в F₁ и F₂ проведем в F, а F₁ и F₂ удалим. Вершины S₁ и S₂ в общем случае удалять нельзя, так как к ним могут идти ребра, но если в S _i возвратов нет, то эту вершину (нетерминал) можно удалить (в нашем примере можно удалить вершину S₂ вместе с выходящими из нее дугами).

Очевидно, что результирующая грамматика G является А-грамматикой. Зачастую она может быть недетерминированной, но перевод А-грамматики из недетерминированной формы в детерминированную уже был рассмотрен ранее.

Конкатенация. В этом случае, получение грамматики-результата сводится к склеиванию начальной вершины S₂ языка-суффикса с заключительной вершиной F₁ языка-префикса, т.е. все ребра, шедшие в F₁, направляются в S₂, а F₁ удаляется (см. рис. 5.3 (а)).

Итерация. Для каждого ребра,идущего из некоторой вершины A исходной грамматики в заключительную вершину F, строится дублирующее его ребро, ведущее из A в начальную вершину S. На рис. 5.3 (б) добавляемые ребра выделены жирной линией.

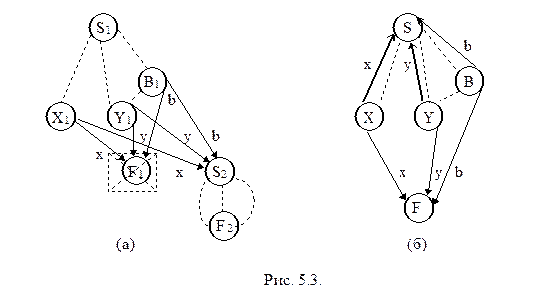
Обращение. На рис. 5.4 (а) представлен граф исходной грамматики. Изменим имя начальной вершины S на S₁ и добавим вершину S₂. Для всех ребер, выходящих из S₁ и входящих в A, добавим дуги, выходящие из S₂ и входящие в A (см. рис. 5.4 (б)). Заменим имя заключительной вершины F на имя начальной S, а имя вершины S₂ на имя заключительной F и изменим ориентацию ребер. В результате мы получим А-грамматику, определяющую обращение исходного языка. Граф этой грамматики представлен на рис. 5.4 (в).

Заметим, что добавление вершины необходимо только в случае возвратов в начальную вершину исходной грамматики. Если возвратов нет, то достаточно изменить ориентацию ребер и сделать перестановку имен начального и заключительного состояний.

Подстановка. На рис 5.5 (а) представлена грамматика G₂ языка L₂, который мы хотим подставить вместо терминала a в язык L₁ с грамматикой G₁, приведенной на рис. 5.5 (б). Возьмем столько экземпляров G₂, сколько в G₁ имеется ребер, помеченных терминалом a. Нетерминалы в G₁ отметим индексом 0, а нетерминалы в i - ом экземпляре G₂ индексом i. На место каждого ребра G₁, помеченного терминалом a и идущего из A₀ в B₀, подставим экземпляр G₂, т.е. вершину A₀ из G₂ совместим с вершиной S_i, а вершину B₀ - с вершиной F_i. Отметим, что при наличии возвратов в начальную вершину грамматики G₂ и других ребер, идущих из A₀ грамматики G₁ и помеченных терминалами, отличными от a, необходимо расщеплять начальную вершину грамматики G₂ на две вершины. Одна из них в точности совпадает с исходной, а другая повторяет все выходы исходной начальной вершины, но возвраты в нее опускаются. Именно эту вторую начальную вершину без возвратов и совмещают с A₀. Результаты этих преобразований приведены на рис. 5.5 (в), отражающем грамматику языка, полученного в результате указанной подстановки.

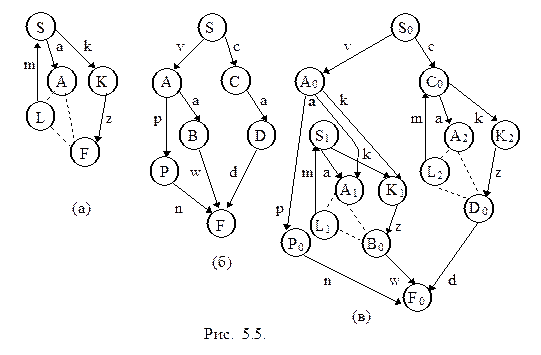
Пересечение. Здесь мы отойдем от принятого выше представления А-грамматик в виде графов состояний и рассмотрим построение грамматики, определяющей пересечение двух А-языков на конкретном примере.

Пример 5.3. Пусть А-язык L₁ определяется А-грамматикой

G₁=( V_T1,V_N1,R₁,S₁ ) и множество R₁ - это группа модифицированных правил

S ® aS ½ bC ½ dC

C ® bC ½ cC ½ûë F,

где F - заключительный нетерминал,

и А-язык L₂ определяется А-грамматикой G₂=( V_T2,V_N2,R₂,S₂ ) и

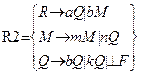
Выполним формальную процедуру операции пересечения.

Определим грамматику G=( V_N, V_T, R, <SR>) языка L = L₁Ç L₂. Для того чтобы проконтролировать наше решение, вначале определим вид цепочек как заданных языков, так и языка - результата, благо простота выбранных грамматик позволяет легко это сделать. Цепочки языка L₁ могут содержать в начале произвольное количество символов a, обязательный символ b или d, затем, возможно, серию символов b и (или) c и в завершении символ ûë. Схематично цепочку языка L₁ можно представить в виде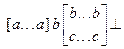, где квадратные скобки ограничивают необязательные части строки, многоточие обозначает произвольное количество символов, а две строки - произвол в выборе символов. Цепочки языка L₂ имеют вид или , а цепочка результирующего языка - .

Заметим, что S Í S₁Ç S₂. Построение грамматики-пересечения напоминает построение детерминированной формы А-грамматики. В качестве элементов нового множества нетерминалов выбираются пары нетерминалов исходных грамматик типа <SR>, <SQ>, <SM>, <CM>, <CQ> и т.п. В результате построения правил грамматики-пересечения часть этих нетерминалов может быть исключена как внутренние или внешние тупики. Схема построения правил новой грамматики состоит в том, что рассматриваются только те пары нетерминалов и те их альтернативы, которые имеют одни и те же терминалы в качестве продолжения цепочки. В результате мы получим грамматику

<SR> ® a<SQ> ½ b<CM>

<SQ> ® b<CQ>

<CQ> ® b<CQ> ½ûë <FF>

Заметим, что нетерминал <CM> не имеет общего продолжения, является внешним тупиком и его можно исключить вместе с правилом <SR> ® b<CM>. †

То есть операция пересечения L=L₁ÇL₂ определяется следующим образом:

G=<V_T1ÇV_T2,V_N={<A₁A₂>,A₁ÎV_N1,A₂ÎV_N2},<S₁S₂>,R={<AB>®a<CD>, если в исходных грамматиках G₁ присутствует правило вида A®aC: A,CÎV_N1, в грамматике G₂ B®aD, B,DÎV_N2} >.

В результате такого построения получается язык, включающий множество цепочек, принадлежащих языку L₁ и L₂. Действительно:

а) если jÎL₁,L₂ и j=ab…f, то отсюда следует, что существует вывод в L₁ и L₂: S₁aA₁bB₁…fF₁ в G₁ и вывод в G₂: S₂aA₂bB₂…fF₂.

По построению, если существуют такие правила вывода, то в L появится правило вида <S₁S₂>a<A₁A₂>…f<F₁F₂>. Если есть такой вывод, то цепочка j принадлежит языку L.

б) Проводя аналогичные рассуждения в обратном порядке, получим, что любая цепочка, принадлежащая языку L, принадлежит языкам L₁ и L₂. †

Рассмотрим еще один пример:

В результате выполнения операции пересечения получим:

– тупик

Дата добавления: 2014-01-11