
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Операции над контекстными языками
|
|
|
|
Теорема. К-языки, так же как и КС-языки, замкнуты относительно операций объединения, конкатенации, итерации, обращения, подстановки и не замкнуты относительно операций пересечения, дополнения и разности.
Доказательство:
Алгоритмы выполнения перечисленных операций аналогичны алгоритмам для КС-языков, кроме операции конкатенации и подстановки.
До выполнения операций конкатенации и подстановки в К-языках выполняется преобразование полутерминалов. Суть этого преобразования состоит в следующем. Каждый из терминальных символов исходных грамматик заменяется на нетерминал, помеченный соответствующим терминальным символом: например, a заменяется на Aa и добавляются правила вида Aa®a. После этого осуществляется индексация нетерминалов исходных грамматик, что приводит к тому, что терминальные символы в разных грамматиках помечаются разными индексами и могут быть получены только в самом конце вывода цепочки, в результате этого контекст исходных грамматик не может привести к выводу цепочек, не принадлежащих результирующему языку.
Например:
G2: S®b G1: S®aA
Ab®cb
A®a
Выполним операцию конкатенации без преобразования полутерминалов, проиндексировав нетерминалы исходных грамматик:
S®S1S2
S2®ab
S1®aA1
A1b®cb
A1®a.
В результате может быть выведена цепочка – acb, не принадлежащая языку. Теперь выполним преобразование полутерминалов и только затем проиндексируем грамматики, в результате чего цепочки, не принадлежащие языку, в грамматике не выводимы:
S®S1S2
S2®Bb2 S1®Aa1A1
A1®a1; A1Bb1®Cc1Bb1
Bb2®b Aa1®a; Bb1®b; Cc1®c
5.3. Выводы для практики
В результате операций над языками получается новое множество цепочек, то есть новый язык, который “собран из кусков”, состоит из частей исходных языков. С практической точки зрения очень важно, что язык можно разложить на более простые языки и формировать сложный язык на базе простых языков и операций над ними. Так, если нам известен язык букв Lб (любая латинская буква) и язык цифр Lц, то можно совершенно тривиально определить язык идентификаторов Lи конкатенацию языка букв и итерацию объединения языка букв и языка цифр:
Lи = Lб (LбÈ Lц ) *.
Отметим, что при реализации на ЭВМ программы синтаксического анализа различных языков лучше всего представлять в виде логических процедур-функций, дающих положительный ответ в случае принадлежности цепочки или ее фрагмента рассматриваемому языку и отрицательный при обнаружении ошибок. При таком построении итерация языка подменяется вызовом соответствующей процедуры внутри цикла; конкатенация - последовательным вызовом процедур анализа составляющих языков; объединение - альтернативным вызовом процедур; подстановка - заменой анализа терминала на процедуру анализа подставляемого языка.
Пример 5.4. Рассмотри простейший язык записи результатов шахматного матча для одного из его участников, цепочки которого имеют вид:
+ победы = ничьи – поражения,
где победы, ничьи и поражения представляются в виде целых констант без знака или имен переменных (идентификаторов). Данный язык
L = L+ Lблок L= Lблок L - Lблок L,
где L + = {+}, L = = {=}, L - = {-}, L блок = L и È L к, Lи = Lб (LбÈ Lц ) *,
L к = Lц+, Lб = {a,b,...,y,z}, Lц = {0,1,...,9}, L;={;}.
Ниже представлена программа на языке Паскаль, реализующая синтаксический анализ цепочек предложенного языка. В ней выделены процедуры-функции анализа букв, цифр, идентификаторов, констант и блоков. Предусмотрен ввод серии строк для анализа, и признаком конца тестирования данного анализатора служит ввод пустой строки. В процессе обработки строк языка осуществляется формирование массивов идентификаторов и констант, которые выводятся по завершению тестирования. Кроме фатальных ошибок, приводящих к завершению обработки текущей строки, предусмотрены сообщения об ошибках - предупреждениях о переполнении констант и идентификаторов. Позиции ошибок вместе с сообщениями о них формируют массив ошибок MEr, который выводится по завершению анализа строки.
program analppn;
uses TPCrt;
type Idn = string[8]; { тип для идентификатора }
CEr = 0..4; { код ошибки }
var
Str: string; { входная строка }
Lst: byte absolute Str; { количество символов в строке }
Ist: word; { индекс по входной строке }
Midn: array [0..100] of idn; { массив идентификаторов }
Mcon: array [0..100] of word; { массив констант }
Imi, Imc: word; { индексы массивов midn и mcon }
s: char; n: byte; { рабочие переменные }
MEr: array [0..4] of string; { строки сообщений об ошибках}
IEr: word; { индекс ошибок }
cod: CEr;
i: word;
const
{ сообщения в программе }
WroIdn = ' Количество символов в идентификаторе > 8-ми';
WroCon = ' Переполнение константы';
ErVic = ' Ошибка в победах';
ErDraw = ' Ошибка в ничьих';
ErDet = ' Ошибка в поражениях';
ErFin = ' Ожидается ";"';
OK = ' Строка синтаксически верна';
Inq = ' Введите строку >';
procedure Blank;
(* пропуск управляющих символов и пробелов *)
begin
while (Ist <= Lst) and (Str[Ist] <= #32) do inc(Ist)
end {Blank};
function Let (s:char): boolean;
(* контроль букв *)
begin
Let:=(UpCase(s) >= 'A') and (UpCase(s) <= 'Z')
end { Let };
function Dig (s: char; var n: byte): boolean;
(* контроль цифр *)
begin
if (s >= '0') and (s <= '9') then begin
n:=ord(s)-48 {-ord('0')}; Dig:=true end
else Dig:=false
end {Dig};
function Ident (var id: Idn): boolean;
(* анализ идентификатора *)
var
i: word;
begin
Blank; i:=Ist; id:=''; Ident:=false;
if Let(Str[Ist]) then begin
while Let(Str[Ist]) or Dig(Str[Ist],n) do begin
if (Ist-i) < 8 then id:=id+Str[Ist];
inc(Ist);
end;
if (Ist-i) > 7 then begin
inc(Ier); MEr[Ier]:=WroIdn; MEr[0,i+7]:='^'
end;
Ident:=true; Blank
end
end {Ident};
function Cons (var c: word): boolean;
(* анализ константы *)
var
ov: boolean; { признак переполнения }
begin Blank;
ov:=false; c:=0; Cons:=false;
while Dig(Str[Ist],n) do begin
Cons:=true;
if not(ov) then
if (c < 6553) or ((c=6553) and (n <= 5)) then c:=c*10+n
else begin
ov:=true; inc(Ier); MEr[Ier]:=WroCon; MEr[0,Ist]:='^'
end;
inc(Ist);
end; Blank;
end {Cons};
function Block (s: char): boolean;
(* анализ блока, начинающегося с символа-параметра s и
содержащего идентификатор или константу в качестве продолжения *)
begin
block:=true; Blank;
if Str[Ist] = s then begin inc(Ist);
if Ident(Midn[Imi]) then inc(Imi)
else
if Cons(Mcon[Imc]) then inc(Imc)
else begin MEr[0,Ist]:='^'; block:=false end
end
else begin MEr[0,Ist]:='^'; block:=false end
end {Block};
function Anal: CEr;
(* анализ строки c возвратом кода ошибки *)
begin
Anal:=0;
if not(Block('+')) then begin Anal:=1; exit end;
if not(Block('=')) then begin Anal:=2; exit end;
if not(Block('-')) then begin Anal:=3; exit end;
if Str[Ist] <> ';' then begin MEr[0,Ist]:='^'; Anal:=4 end
end {analizer};
procedure Parser;
(* анализ с выдачей сообщений об ошибках *)
begin
Ier:=0; Ist:=1;
FillChar(MEr[0,1],80,' '); MEr[0,0]:=#80;
cod:=Anal;
WriteLn(MEr[0]);
for i:=1 to Ier do
WriteLn(MEr[i]);
case cod of
0: WriteLn(OK);
1: WriteLn(ErVic);
2: WriteLn(ErDraw);
3: WriteLn(ErDet);
4: WriteLn(ErFin)
end
end {Parser};
begin
Imi:=0; Imc:=0;
while true do begin
WriteLn(Inq);
ReadLn(Str);
IF Lst = 0 then break;
Parser;
end;
if (Imi > 0) or (Imc > 0) then begin
WriteLn(' ИДЕНТИФИКАТОРЫ КОНСТАНТЫ');
i:=0;
repeat
if i < Imi then Write(Midn[i]:11)
else Write(' ':11);
if i < Imc then Write(Mcon[i]:15);
WriteLn; inc(i);
until (i >= Imi) and (i >= Imc)
end;
ReadKey;
end. ›
5.4. Неоднозначность КС-грамматик и языков
Напомним, что КС-грамматика G неоднозначна, если существует цепочка aÎL(G), имеющая два или более различных деревьев вывода. Если грамматика используется для определения языка программирования, желательно, чтобы она была однозначной. В противном случае программист и компилятор могут по-разному понять смысл некоторых программ. Неоднозначность - нежелательное свойство КС-грамматик и языков.
Пример неоднозначной КС-грамматики арифметических выражений был рассмотрен в параграфе 1.1. Но самый известный пример неоднозначности в языках программирования - это “кочующее else ”.
Пример 5.5. Рассмотрим грамматику с правилами вывода
S ® if b then S else S ½ if b then S ½ a
Эта грамматика неоднозначна, так как цепочка
if b then if b then a else a
имеет два дерева вывода, первое из которых (рис 5.6 (а)) предполагает интерпретацию
if b then (if b then a) else a,
а второе (рис 5.6 (б))-
if b then (if b then a else a)
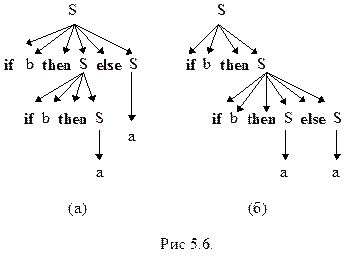 –
–
Хотелось бы иметь алгоритм, который по произвольной КС-грамматике выяснял, однозначна она или нет. Но, к сожалению, можно доказать, что проблема - однозначна ли КС-грамматика G - алгоритмически неразрешима. Хотя такого алгоритма нет, можно указать некоторые встречающиеся в правилах конструкции, приводящие к неоднозначности, которые можно распознать на практике и избегать при описании языков программирования.
Грамматика, содержащая правила A ® AA ½ a, неоднозначна, так как подцепочка AAA допускает два различных разбора (рис. 5.7).
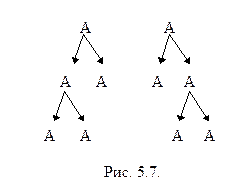
Здесь можно устранить неоднозначность, если вместо предложенных правил с двухсторонней рекурсией использовать одностороннюю, то есть использовать правила:
A ® AB ½ B
B ® a
или правила
A ® BA ½ B
B ® a
Другой пример неоднозначности - правило A ® AaA, так как цепочку AaAaA можно получить по двум разным деревьям вывода. Пара правил
A ® aA ½ Ab тоже создает неоднозначность - цепочка aAb имеет два разных левых вывода A Þ aA Þ aAb и A Þ Ab Þ aAb.
Все перечисленные примеры так или иначе связаны с двухсторонней рекурсией. Более тонкий пример - пара правил A ® aA ½ aAbA, по которым цепочка aaAbA имеет два вывода A Þ aAbA Þ aaAbA и A Þ aA Þ aaAbA. Если при двухсторонней рекурсии средством борьбы с неоднозначностью является устранение рекурсии с одной из сторон, то в последнем случае поможет левая факторизация.
Из приведенных примеров ясно, что определенная выше неоднозначность - это свойство грамматики, а не языка. Для некоторых неоднозначных грамматик можно построить эквивалентные им однозначные грамматики.
Пример 5.6. Рассмотрим грамматику из примера 5.5. Эта грамматика неоднозначна потому, что else можно ассоциировать с двумя различными then. Неоднозначность можно устранить, если связать else с последним из предшествующих ему then, как на рис. 5.6 (б). Для этого введем два нетерминала S1 и S2 с тем чтобы S2 порождал только полные операторы вида if-then-else, а S1 - операторы обоих видов. Правила новой грамматики имеют вид
S1 ® if b then S1 ½ if b then S2 else S1 ½ a
S2 ® if b then S2 else S2 ½ a
Тот факт, что слову else предшествует только S2, гарантирует появление внутри конструкции then-else либо символа a, либо другого else. Таким образом, структура, изображенная на рис. 5.6 (а), здесь не возникает. –
КС-язык называется неоднозначным (или существенно неоднозначным), если он не порождается никакой однозначной КС-грамматикой.
С первого взгляда не видно, существуют ли вообще неоднозначные КС-языки, но нашим следующим примером и будет такой язык.
Пример 5.7. Пусть L= {a i b j c k ½ i = j или j = k }. Этот язык неоднозначен, что можно строго доказать. Интуитивно же это объясняется тем, что цепочки с i = j должны порождаться группой правил, отличных от правил, порождающих цепочки с j = k. Тогда, по крайней мере, некоторые из цепочек с i = j = k должны порождаться обоими механизмами. Одна из КС-грамматик, порождающих L, такова:
S ® AB ½ DC
A ® aA ½ e
B ® bBc ½ e
C ® cC ½ e
D ® aDb ½ e
Ясно, что она неоднозначна и на рис. 5.8 представлены два дерева вывода цепочки aabbcc. Проблема, порождает ли данная КС-грамматика однозначный язык (т.е. существует ли эквивалентная ей однозначная грамматика), алгоритмически неразрешима. Но для некоторых больших подклассов КС-языков известно, что они однозначны. Именно к этим подклассам и относятся все созданные до сих пор языки программирования.
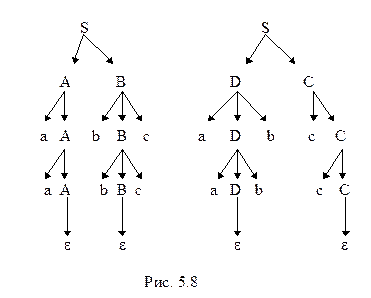
Упражнения
5.1. Покажите, что следующие языки не являются А-языками:
(а) {0 n 1 0 n | n ³ 1},
(б) {ww | w Î {0,1} * }
(в) L(G), где G определено правилами S ® aSbS ½ c.
5.2. Покажите, что следующие языки не контекстно-свободны:
(а) {a i b i c j | j £ i};
(б) {a i b j c k | i < j < k};
(в) {a i b j a j b i | j £ i};
(г) {a m b n a m b n | m, n ³ 1};
(д) {a i b j c k | все числа i, j, k разные}
5.3. Пусть имеется следующая серия непересекающихся языков: Lми - язык мужских имен - {Миша, Андрей, Петя,... }, Lжи - язык женских имен - {Марина, Таня, Катя,... }, Lси - язык “средних” имен - {Валя, Саша, Женя,... }, Lмф - язык мужских фамилий - {Шамашов, Сидоров, Петров,... }, Lжф - язык женских фамилий - {Наянова, Михеева, Соловьева,... } и язык “средних” фамилий Lсф = {Кричевер, Пономаренко, Перебейнос,... }. Требуется с помощью операций над заданными языками построить язык L - всех правильных сочетаний имен и фамилий. Попробуйте оптимизировать вашу запись.
5.4. С помощью операций над языками постройте язык L - правильных процедур Паскаля, если имеются: язык заголовков, начала и концов процедур Lp, Lbegin, Lend; языки описания переменных Lvar, Lconst, Ltype; языки операторов присваивания L:=; ветвлений - Lif, Lcase; циклов Lwhile, Lfor и т.п. При этом считается, что перечисленные языки охватывают всю рассматриваемую конструкцию.
5.5. Пусть имеется язык заголовков цикла - Lwhile, языки начала и конца блоков Lbegin и Lend, язык оператора присваивания L:=. Постройте язык циклов L, считая, что тело цикла могут составлять операторы присваивания, вложенные или/и чередующиеся циклы данного типа.
5.6. Постройте грамматики объединения, итерации, конкатенации, обращения, подстановки и пересечения языков со следующими правилами грамматики:
G1: S ® aA ½ bB ½ c G2: S ® aA
A ® aS ½ a A ® bA ½ bC
B ® b C ® kA ½ cS ½ d
а) рассматривая исходные языки как КС-языки,
б) рассматривая их как А-языки.
Глава 6. СИНТАКСИЧЕСКИЙ АНАЛИЗ КС-ЯЗЫКОВ
6.1. Методы анализа КС-языков. Грамматики предшествования.
6.2. Грамматики предшествования Вирта.
6.3. Грамматики предшествования Флойда.
6.4. Функции предшествования.
Упражнения.
6.1.Методы анализа КС-языков. Грамматики предшествования
В А-грамматике синтаксический анализ цепочки прост: начиная с первого символа цепочки, переходя из состояния в состояние, делается вывод о возможности получения очередного символа цепочки, либо о переходе автомата в ошибочное состояние. Для вывода цепочки aaaa в грамматике S®aS|a необходимо выполнить следующую последовательность действий: aS®aaS®aaaS®aaaa, предварительно приведя грамматику к детерминированной форме. В КС-грамматиках используется дерево вывода и грамматики также могут быть неодназначными.
Большинство языков программирования можно описать с помощью контекстно-свободных грамматик. Но построить алгоритм анализа по таким грамматикам в общем случае не так просто и эти алгоритмы, как правило, неэффективны. Один из путей анализа цепочек КС-языка следует из теоремы о разрешимости таких языков. Напомним, что любой КС-язык можно описать с помощью КС-грамматики в удлиняющей форме, по которой любая цепочка заданного языка длины n выводится не более чем за n шагов. Для того чтобы определить принадлежность некоторой цепочки с длиной n данному языку, необходимо по заданной грамматике вывести все бесповторные цепочки, которые выводятся не более чем за n шагов, и сравнить их с исходной цепочкой. Если мы обнаружим совпадение, то исходная цепочка принадлежит языку, в противном случае – не принадлежит. Совершенно очевидно, что подобный потенциально осуществимый алгоритм не имеет практического смысла. Во-первых, необходимо строить вывод миллиардов цепочек, во-вторых, такой алгоритм может ответить только на вопрос принадлежности языку. Локализовать и идентифицировать ошибку, а тем более осуществить трансляцию в процессе синтаксического анализа текста он не способен.
Методы построения анализаторов по КС-грамматике делятся на две группы: нисходящие (анализ сверху вниз) и восходящие (анализ снизу вверх). Эти термины соответствуют способу построения синтаксических деревьев вывода.
Нисходящие методы выполняют анализ с начального выделенного нетерминала или, иначе, от корня дерева вывода вниз, к концевым вершинам, пытаясь построить дерево вывода цепочки. Если дерево удалось построить, то цепочка принадлежит языку, в противном случае – не принадлежит. В общем случае все методы основаны на переборе всех возможных вариантов вывода, поэтому неэффективны, хотя и существуют алгоритмы нисходящего разбора с возвратами, ограничивающие число переборов вариантов при выводе цепочек.
Алгоритмы восходящего разбора начинаются с листьев дерева вывода (с входных символов, как и в автоматных грамматиках) и пытается построить дерево разбора, восходя от листьев к корню. Среди этих алгоритмов наиболее эффективными являются алгоритмы, использующие при свертке отношения предшествования.
В цепочке КС-языка сложно выделить основу для свёртки. В 1966 г. Вебером впервые был предложен метод свёртки с использованием отношения предшествования. Согласно этому методу между любыми символами, которые могут встретиться на любом шаге вывода цепочки, определяется одно из трёх отношений предшествования:
 – отношение предшествования равенства,
– отношение предшествования равенства,
отношение предшествования меньше (раньше): <×
и отношение предшествования больше (позже): × >
Между любыми двумя символами S1 и S2 устанавливается отношение 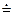 , если они находятся рядом в одном правиле вывода.
, если они находятся рядом в одном правиле вывода.
S1<·S2, если S1 уже выведено, а S2 – будет стоять рядом с S1 при применении некоторого правила на следующем шаге вывода.
S1·>S2 (S1 “позже” S2), если S2 выведено, а S1 будет стоять рядом с S2 на следующем шаге вывода.
Основа для свёртки – множество символов, находящихся между отношениями предшествования <· и ·>.
Наиболее эффективные методы свертки применимы для узкого класса КС-грамматик, называемых грамматиками предшествования, для которых выполняются следующие ограничения.
Грамматики предшествования – узкий класс КС-грамматик, в которых:
1) между любыми символами существует не более одного отношения предшествования;
2) не существует правил с одинаковыми правыми частями.
В классе грамматик предшествования существует несколько видов грамматик, различающихся правилами определения отношений предшествования между символами. Существуют грамматики простого и расширенного предшествования в зависимости от того, за сколько шагов при выводе цепочек определяется отношение предшествования. Кроме этого отношения предшествования могут устанавливаться между различными символами. Далее будут рассмотрены грамматики простого предшествования Вирта и грамматики операторного предшествования Флойда.
6.2. Грамматики предшествования Вирта
Рассмотрим грамматику предшествования Вирта.
Отношения предшествования определяются между любыми символами: как терминальными, так и нетерминальными.
Алгоритм свёртки терминальных цепочек по Вирту:
1. Строится для любого нетерминального символа множество левых и правых символов.
2. Определяется отношение предшествования между символами и заносится в матрицу (таблицу предшествования).
3.Выполняя последовательные выделения основ для свёртки, осуществляется собственно свёртка цепочек.
4. Включается семантика в алгоритм свёртки цепочки.
Множество левых и правых символов для каждого нетерминала грамматики определяются следующим образом:
L – множество левых символов:
L(u)={S|u®SjÚ(u®AjÙSÎL(A)),
uÎVN,, SÎ(VTÈVN), jÎ(VTÈVN)* }
R – множество правых символов:

Отношения предшествования в грамматике по Вирту определяются следующим образом:
а) S1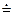 S2, если существует правило вида: u®jS1S2h, где u – нетерминал, S1,S2Î(VTÈVN), j,hÎ(VTÈVN)*.
S2, если существует правило вида: u®jS1S2h, где u – нетерминал, S1,S2Î(VTÈVN), j,hÎ(VTÈVN)*.
б) S1< ·S2, если существует правило вида: u®jS1Bh, S2ÎL(B), S1,S2Î(VTÈVN), u,BÎVN, j,hÎ(VTÈVN)*
в) S1 ·>S2, если существует правило вида: u®jAS2h, S1ÎR(A), S1,S2Î(VTÈVN), u,AÎVN, j,hÎ(VTÈVN)* или u®jABh, S1ÎR(A), S2ÎL(B), A,B,uÎVN
Пример 6.1.
S®^(AB)^, A®[A]|*, B®[B]|+
Строим множество левых и правых символов (рис. 6.1).
| U | L(u) | R(u) |
| S | ^ | ^ |
| A | [* | ]* |
| B | [+ | ]+ |
Рис. 6.1
| S | ^ | ( | A | B | ) | [ | ] | * | + | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| S | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ^ | 
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ( | 
| <· | <· | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| A | 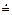
| <· | 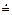
| <· | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| B | 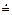
| 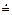
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ) | 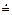
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [ | 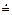
| 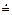
| <· | <· | <· | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ] | ·> | ·> | ·> | ·> | ·> | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | ·> | ·> | ·> | ·> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | ·> | ·> |
Матрица предшествования изображена на рис.6.2.
Рис. 6.2
Проверим принадлежность цепочки 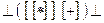 языку, выполнив свертку по Вирту:
языку, выполнив свертку по Вирту:
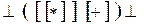


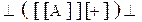
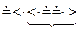
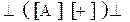
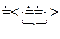
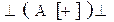
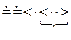
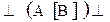

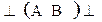 -
-
S Рис. 6.3
Как видно удалось свернуть цепочку до начального выделенного символа S, значит цепочка принадлежит языку. Цепочка 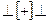
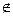 языку.
языку.
При выполнении свертки по Вирту возможны следующие ошибки:
1)между двумя символами не существует отношения предшествования;
2)выделена основа для свертки, а подходящего правила для замены нет.
Не существует общего алгоритма, позволяющего преобразовать произвольную КС-грамматику к грамматике предшествования, хотя существует правило, позволяющее выполнить это для некоторых КС-грамматик, действие которого показано на следующем примере:
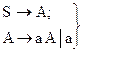

Включение семантики осуществляется следующим образом: в соответствии с любым правилом вывода ставится некоторое семантическое действие, которое выполняется при замене основы для свертки на это правило.
6.3. Грамматики предшествования Флойда
Отношения предшествования в грамматиках операторного предшествования Флойда определяются только между терминальными символами, причём в правилах вывода не допускаются два рядом стоящих нетерминала:  .
.
Алгоритм свертки по Флойду включает те же пункты, что и алгоритм свертки по Вирту.
 |
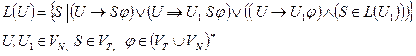

Отношения предшествования между любыми терминальными символами S1 и S2 определяются следующим образом:
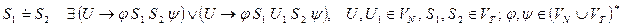
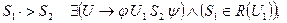
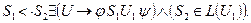
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1294; Нарушение авторских прав?; Мы поможем в написании вашей работы!