
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 6.2
|
|
|
|





| ^ | + | * | a.z | ( | ) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ^ | 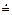
| <· | <· | <· | <· | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| + | ·> | ·> | <· | <· | <· | ·> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | ·> | ·> | ·> | <· | <· | ·> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a..z | ·> | ·> | ·> | ·> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ( | <· | <· | <· | <· | 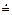
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ) | ·> | ·> | ·> | ·> |
Матрица предшествования представлена на рис. 6.4.
Рис. 6.4
Выполним свертку по Флойду цепочки - 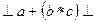
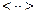
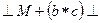
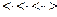
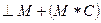 ^
^
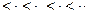 >
>
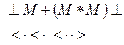
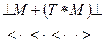
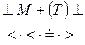
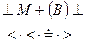
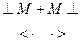
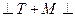 ,
, ,
,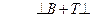 ,
, 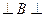

Рис. 6.5
Таким образом, можно сделать вывод, что цепочка принадлежит языку.
По сравнению с грамматикой Вирта, в грамматиках по Флойду матрица предшествования гораздо меньше, но алгоритм свертки работает гораздо дольше из-за необходимости перебора всех правил вида A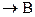 . Ошибки при свертке про Флойду возникают в следующих случаях:
. Ошибки при свертке про Флойду возникают в следующих случаях:
если между двумя символами, стоящими рядом на одном из шагов вывода цепочки, нет отношения предшествования;
если для выделенной основы для свертки выполнены все переборы, а соответствующих правил для замены в грамматике нет.
Введение семантики в грамматику по Флойду осуществляется так же, как в грамматиках по Вирту.
6.4 Функции предшествования
В грамматиках алгоритмических языков число терминальных и нетерминальных символов превышает 200-300, поэтому таблица предшествования занимает большой объём памяти. Для уменьшения этого объёма было предложено вместо таблицы предшествования использовать функции предшествования - числовые функции нечислового аргумента, которые определяются следующим образом:
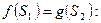
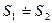
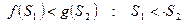
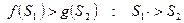
Рассмотрим метод графов построения функции предшествования.
В соответствии с таблицей предшествования граф строится следующим образом (рис. 6.6): для каждого символа (отношения предшествования в таблице предшествования) определяются две вершины 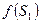 и
и 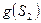 , причём, если для некоторых символов
, причём, если для некоторых символов 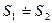 , то
, то 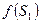 и
и 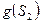 объединяются в одну вершину. Если между символами
объединяются в одну вершину. Если между символами 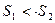 , то на графе они будут связаны таким образом:
, то на графе они будут связаны таким образом:
| |||||
 | |||||
 | |||||
Рис. 6.6
После построения графа выполняется следующая последовательность действий:
1. Все вершины, для которых нет потомков, помечаются индексом “1” и удаляются из рассмотрения вместе с входящими в них дугами.
2. Вершины, у которых все потомки помечены, помечаются значениями на единицу больше, чем максимальный индекс его потомков, после этого эти вершины удаляются из рассмотрения вместе с входящими в них дугами.
|
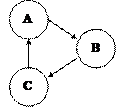
Рис. 6.7
На рис. 6.8 показан граф и построена функция предшествования для таблицы предшествования из примера 6.2.
Рассмотрим ещё один способ построения функций предшествования - метод инкрементов:
1) Все значения 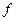 и
и 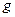 приравниваем к единице.
приравниваем к единице.
2) Значения функции предшествования изменяются в большую сторону следующим образом:
если 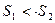 , то
, то 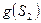 =
=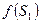 +1;
+1;
если 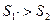 , то
, то 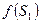 =
=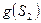 +1;
+1;
|
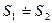
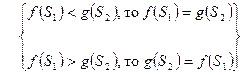
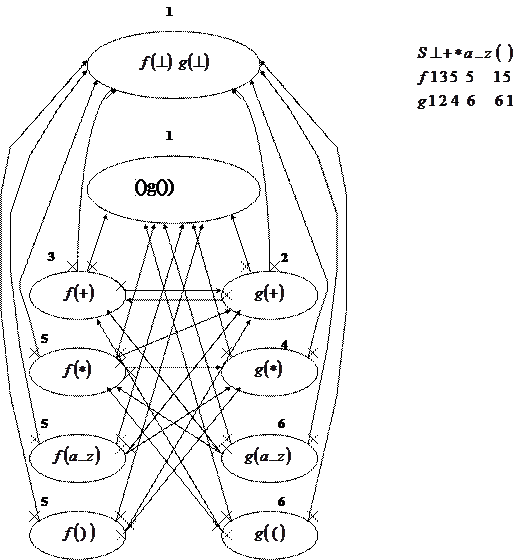 |
Рис.6.8
|
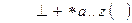
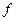 1 1 1 1 1 1
1 1 1 1 1 1
|
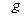 1 1 1 1 1 1
1 1 1 1 1 1
|
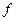 1 3 5 5 1 5
1 3 5 5 1 5
|
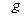 1 2 4 6 6 1
1 2 4 6 6 1
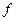 1 3 5 5 1 5
1 3 5 5 1 5
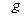 1 2 4 6 6 1
1 2 4 6 6 1
Функция предшествования не существует, если значения ее получаются больше, чем величина 2n, где n- общее число символов матрицы предшествования.
Упражнения
6.1. Построить отношения простого предшествования для грамматики с правилами
S ® aSbôcôd.
6.2. Построить отношения простого предшествования и функцию предшествования, используя граф линеаризации, для грамматики с правилами S ® aSSbôcôd. Покажите этапы свертки фраз aacdbcb, ab, acb.
| ·> | ·> | ·> | ||
| ·> | ·> | |||
| <· | 
| <· | ||

| 
|
6.3. Определить, является ли грамматика логических выражений, правила которой приведены ниже, грамматикой простого предшествования Вирта. Если она таковой не является, то преобразовать ее, построить для нее отношения простого предшествования и функцию предшествования, используя метод графов.
E ® E or TôT
T ® T and MôM
M ® aô(E) ônot M
6.4. Постройте отношения простого предшествования для грамматики с правилами
S ® 0S11ô011 и терминалами { 0, 1 }. Если данная грамматика не является грамматикой простого предшествования, то преобразуйте ее к такой грамматике.
6.5. Постройте отношения операторного предшествования и функцию предшествования, используя методы графов и инкрементов для грамматики из упражнения 6.4.
6.6. Преобразуйте грамматику S ® E
E ® TôTBEô(E)
T® aôbô¼ôz
B®+ï-½*ô/ к грамматике простого предшествования Вирта. Покажите этапы свертки фразы a*(b+c).
6.7. Написать матрицу предшествования Флойда для грамматики:
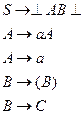
С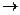 0| …|9|0C|…|9C
0| …|9|0C|…|9C
и проанализировать цепочку: 1) 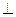 aa(((039)))
aa(((039))) 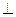 2)
2) 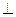 aa(497))
aa(497)) 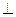
Глава 7. ВВЕДЕНИЕ В СЕМАНТИКУ
7.1. Польская инверсная запись.
7.2. Интерпретация ПОЛИЗа.
7.3. Генерирование команд по ПОЛИЗу.
7.4. Алгоритм Замельсона и Бауэра перевода выражений в ПОЛИЗ.
7.5. Атрибутные грамматики.
Упражнения
Обычно в компиляторах и интерпретаторах каждому правилу грамматики, каждой альтернативе любого нетерминала ставятся в соответствие семантические подпрограммы. Эти подпрограммы выполняются при синтаксических редукциях по заданным правилам грамматики в восходящем разборе или отождествлении фрагмента входной цепочки с некоторой альтернативой продукции при разборе нисходящем.
В тех случаях, когда исходный язык программирования достаточно сложен или к компилятору предъявляются повышенные требования (например, необходима машинно–независимая оптимизация исходной программы с целью получения более эффективного объектного кода), первоначально исходная программа переводится в некоторую внутреннюю форму, более удобную для простой машинной обработки. В большинстве внутренних представлений операторы располагаются в том порядке, в котором они должны выполняться, что существенно облегчает последующий анализ, интерпретацию или генерацию объектного кода.
Все внутренние представления программы обычно содержат элементы двух типов: операторы и операнды. Различия представлений состоят лишь в том, как эти элементы объединяются между собой. В дальнейшем мы будем использовать такие традиционные операторы, как +, -, /, MOD, DIV, *, AND, OR, >, <, = и т. п., а также БП (Безусловный Переход) и УПЛ (Условный Переход по Лжи), точнее, условный переход в том случае, когда значение операнда (логического выражения) – ложь (FALSE, 0). Внутри компилятора, конечно же, все они представляются соответствующими лексемами или целочисленными кодами.
Операнды, с которыми мы будем иметь дело, – это простые идентификаторы (имена переменных, процедур и т.п.), константы, временные переменные, генерируемые самим компилятором, и переменные с индексами.
7.1. Польская инверсная запись
Вместо традиционного инфиксного (скобочного) представления арифметических и логических выражений в различных вычислителях часто используется польская инверсная запись (ПОЛИЗ), которая просто и точно указывает порядок выполнения операций без использования скобок. В этой записи, впервые примененной польским математиком Я. Лукашевичем, операторы располагаются непосредственно за операндами, над которыми они выполняются в порядке их выполнения. Поэтому иногда ПОЛИЗ называют суффиксной, или постфиксной записью. Например, A+B записывается как AB+, A*B+C – как AB*C+, A*(B+C/D) – как ABCD/+*, а A*B+C*D – как AB*CD*+.
Остановимся на простейших правилах, которые позволяют переводить в ПОЛИЗ вручную:
1. Идентификаторы и константы в ПОЛИЗе следуют в том же порядке, что и в инфиксной записи.
2. Операторы в ПОЛИЗе следуют в том порядке, в каком они должны вычисляться (слева направо).
3. Операторы располагаются непосредственно за своими операндами.
Таким образом, мы могли бы записать следующие синтаксические правила:
<операнд>::=идентификаторôконстантаô<операнд><операнд><оператор>
<оператор>::=+ô-ô*ô/ô¼
Унарный минус и другие унарные операторы можно представить двумя способами: либо записывать их бинарными операторами, то есть вместо -B писать 0-B, либо для унарного минуса можно ввести новый специальный символ, например @, и использовать еще одно синтаксическое правило <:операнд>::=<операнд>@. Таким образом, выражение A+(-B+C*D) мы могли бы записать AB@CD*++.
С равным успехом мы могли бы ввести префиксную запись, где операторы стоят перед операндами. Таким образом, арифметическое выражение, а далее мы покажем, что не только его, но и любую управляющую конструкцию, можно представить в трех формах записи: префиксной, инфиксной (обычная запись, где операторы располагаются между операндами, а круглые скобки позволяют изменять приоритет операций) и постфиксной. Человек традиционно использует инфиксную запись, тогда как для автоматического вычисления выражений самым удобным способом представления является постфиксная запись или ПОЛИЗ.
ПОЛИЗ расширяется достаточно просто. Нужно только придерживаться правила, что за операндами следует соответствующий им оператор. Так, присваивание <переменная>:=<выражение> в ПОЛИЗе примет вид <переменная><выражение>:=. Например, присваивание А:=B*C+D*100 запишется в ПОЛИЗе как АBC*D100*+:=.
Индексированную переменную в ПОЛИЗе, а точнее вычисление ее адреса можно представить в виде:
идентификатор<индексные выражения>константа[,
где [ – обозначает знак операции вычисления индекса, идентификатор – имя (базовый адрес) индексированной переменной, а константа – количество индексов (мерность массива). Так, переменную A[i,j+k] можно представить в виде Аijk+2[.
Условный оператор
IF <выр> THEN <инстр 1> ELSE <инстр 2>
в ПОЛИЗе будет иметь вид:
<выр> < m > УПЛ <инстр 1> < n > БП <инстр 2>,
где
· <выр> – логическое выражение (условие), которое может принимать значения – 0 (FALSE, ложь) или 1 (TRUE, истина);
· < m > – номер (место, позиция, индекс) символа ПОЛИЗа, с которого начинается <инстр 2>;
· УПЛ (Условный Переход по Лжи) – оператор с двумя операндами <выр> и < m >, смысл которого состоит в том, что он изменяет традиционный порядок вычислений и осуществляет переход на символ строки ПОЛИЗа с номером
< m >, если (и только если) <выр> – ложно (равно 0);
· < n > – номер символа, следующего за <инстр 2>;
· БП (Безусловный Переход) – оператор с одним операндом < n >, который также изменяет порядок вычислений по ПОЛИЗу и осуществляет переход на символ с номером < n >.
Операторы условного и безусловного перехода, как в свое время было показано Дейкстрой, составляют основу внутреннего представления любой структурной управляющей конструкции (циклов типа FOR, WHILE, REPEAT, оператора выбора и т.п.). В рассматриваемых нами примерах потребуется только один условный оператор – УПЛ, хотя никто не мешает определить целую группу таких операторов (смотри, например, мнемонику команды условного перехода языка ассемблера для ПЭВМ с процессором Intel 8086).
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 701; Нарушение авторских прав?; Мы поможем в написании вашей работы!
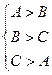 , то функция предшествования не существует.
, то функция предшествования не существует.