
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
ТЕМА: Кинематический анализ механизмов
|
|
|
|
ЛЕКЦИЯ 5
Краткое содержание: Теорема о сложении движения. Кинематический анализ рычажных механизмов методом векторных уравнений и их графическое решение в форме планов положений, скоростей и ускорений. Пример кинематического исследования шарнирного, кривошипно-ползунного и кулисного механизмов.
Контрольные вопросы.
Теорема о сложении движения
При кинематическом исследовании методом планов скоростей и ускорений различают абсолютное и относительное движение звеньев и кинематических пар механизма и основываются на теореме о сложении движения, согласно которой «движение любой точки звена рассматривается как сложное, состоящее из двух движений: а) переносного вместе с одной из точек звена, выбранной за полюс в относительном движении и б) относительного вокруг выбранного полюса»
Абсолютное движение – это движение точки или тела относительно неподвижной системы координат, связанной с неподвижной стойкой
Относительное движение – это движение точки или звена относительно подвижной системы координат, которая связана с каким-либо движущимся звеном. Движение подвижной системы координат называется переносным движением.
Метод векторных уравнений и их графическое решение в форме планов положений, скоростей и ускорений.
Планом положения механизма называется чертеж, изображающий расположение его звеньев в какой-либо определенный момент движения. Отсюда следует, что план положения представляет собой кинематическую схему механизма, вычерченную для заданного положения кривошипа в определенном масштабе.
Планы положений механизмов, включающих в себя двухповодковые группы, строятся методом засечек.
Пример: Построить план положения механизма (рис. 5.1) для заданного угла поворота φ кривошипа при lO A= 0,03 м; lO
A= 0,03 м; lO O
O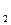 = 0,055 м; lАВ - 0,05 м; l O
= 0,055 м; lАВ - 0,05 м; l O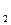 В=0,045м; lAC = lBC = 0,027 м; lO
В=0,045м; lAC = lBC = 0,027 м; lO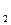 D= 0,024 м; lDE = 0,06 м; смещение
D= 0,024 м; lDE = 0,06 м; смещение 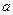 =0,015 м и угол
=0,015 м и угол 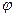 = 55°.
= 55°.
Для построения плана принимаем, что длину кривошипа lO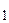 A на схеме будет изображать отрезок O 1 A, длина которого равна 30 мм. Тогда масштаб длин плана
A на схеме будет изображать отрезок O 1 A, длина которого равна 30 мм. Тогда масштаб длин плана
 м/мм.
м/мм.
Затем вычисляем длины остальных отрезков, которые будем откладывать на чертеже:
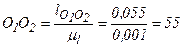 мм;
мм; 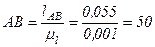 мм;
мм;  мм;
мм;
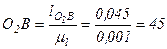 мм;
мм;  мм;
мм;
 мм;
мм; 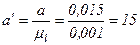 мм.
мм.
Построение плана (рис. 5.1) начинаем с нанесения элементов неподвижного звена. Штрихпунктирной линией проводим линию центров O1O2 и на ней наносим точки O1 и O2 на расстоянии O1O2 = 55 мм. На расстоянии а' от линии O1O2 проводим траекторию движения точки Е.
Под углом φ = 55° к линии O1O2 через точку О1 проводим ось ведущего звена и от этой точки откладываем на ней отрезок О1А. Это и будет изображение ведущего звена О1A в заданном положении.
Положение точки В определяем методом засечек. Для этого из точки А радиусом АВ, а из точки O2 радиусом О2B проводим дуги. Точка их пересечения и будет точкой В.
На звене O2В находим положение точки D. Сделав радиусом DE из точки D засечку на траектории движения точки Е, определяем положение этой точки на схеме. Положение точки С находим на пересечении дуг радиусов АС и ВС.

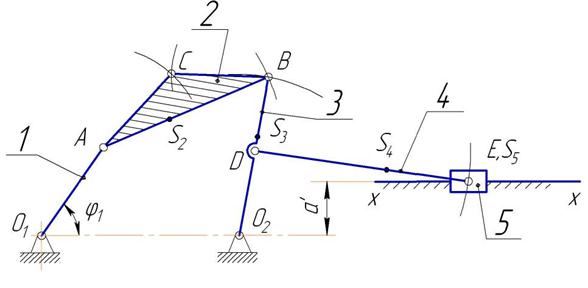 |
Рис. 5.1
Планы скоростей. Зная закон движения ведущего звена и длины всех звеньев механизма, можно определить скорости его точек по величине и направлению в любом положении механизма путем построения плана скоростей для этого положения.
Построение планов скоростей и чтение их во многом упрощаются при использовании свойств этих планов, которые заключаются в следующем:
1. Векторы, исходящие из полюса, изображает абсолютные скорости соответствующих точек звеньев механизма в масштабе плана скоростей. Точки плана скоростей, соответствующие неподвижным точкам механизма, находятся в полюсе плана.
2. Векторы, соединяющие концы векторов абсолютных скоростей, выражают величины и направления относительных скоростей.
3. Векторы относительных скоростей точек звена на плане скоростей образуют фигуру, подобную одноименной жесткой фигуре, образованной отрезками, соединяющими эти точки звена на плане механизма, повернутую по отношению к последней на 90° в сторону мгновенного вращения данного звена.
Пример Определить абсолютные и относительные скорости точек звеньев и угловые скорости звеньев механизма (см. рис. 5.2) методом планов скоростей, кривошип O1A имеет частоту вращения n1 = 120 об/мин в направлении по часовой стрелке. Размеры звеньев — те же.
Решение. Определяем угловую скорость кривошипа О1А по формуле:
 1/c.
1/c.
Согласно теореме о сложении движения абсолютная скорость точки А кривошипа О1А будет определятся
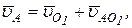
где 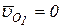 - переносная скорость т. О1,
- переносная скорость т. О1, 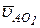 - относительная скорость т. А во вращении вокруг т. В. Т. о., абсолютная скорость совпадает с относительной, поэтому скорость точки А находим по формуле
- относительная скорость т. А во вращении вокруг т. В. Т. о., абсолютная скорость совпадает с относительной, поэтому скорость точки А находим по формуле
 м/с.
м/с.
Вектор  a направлен перпендикулярно к оси звена O1A в сторону его вращения.
a направлен перпендикулярно к оси звена O1A в сторону его вращения.
Задаемся длиной отрезка ра, который будет изображать на плане скорость 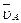 , точки A; ра = 66 мм. Масштаб плана скоростей
, точки A; ра = 66 мм. Масштаб плана скоростей
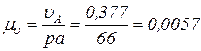 м/с·мм.
м/с·мм.
От произвольной точки р, принятой за полюс плана скоростей, откладываем перпендикулярно к звену О1А отрезок ра (рис. 5.3).
Скорости неподвижных точек О1 и O2 равны нулю, поэтому векторы 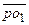 и
и  также равны нулю и, следовательно, токи о1 и о2 на плане скоростей совпадают с полюсом р.
также равны нулю и, следовательно, токи о1 и о2 на плане скоростей совпадают с полюсом р.
Для определения скорости точки В воспользуемся векторными уравнениями:
 (1)
(1)
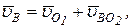 (2)
(2)
где 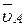 — скорость точки А в переносном движении;
— скорость точки А в переносном движении; 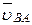 — относительная скорость точки В во вращении вокруг точки А;
— относительная скорость точки В во вращении вокруг точки А; 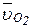 — скорость точки O 2;
— скорость точки O 2; 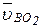 — относительная скорость точки В во вращении вокруг точки O 2.
— относительная скорость точки В во вращении вокруг точки O 2.
В этих уравнениях скорость 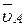 известна по величине и направлению, скорость
известна по величине и направлению, скорость 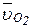 = 0. Относительные скорости
= 0. Относительные скорости 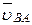 и
и 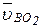 известны лишь по линии действия:
известны лишь по линии действия: 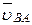 перпендикулярна к звену АВ,
перпендикулярна к звену АВ, 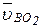 перпендикулярна к звену 02В. Поэтому для определения скорости
перпендикулярна к звену 02В. Поэтому для определения скорости 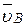 точки В через точку а (конец вектора скорости
точки В через точку а (конец вектора скорости 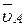 ) проводим перпендикулярно звену АВ линию действия скорости
) проводим перпендикулярно звену АВ линию действия скорости 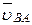 , а через точку о 2, совпадающую с полюсом р плана скоростей, проводим перпендикулярно звену О2В линию действия скорости
, а через точку о 2, совпадающую с полюсом р плана скоростей, проводим перпендикулярно звену О2В линию действия скорости 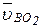 . На пересечении этих двух линий действия получим точку b — конец вектора скорости
. На пересечении этих двух линий действия получим точку b — конец вектора скорости 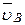 точки В:
точки В:
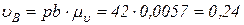 м/с.
м/с.
Направление скорости 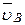 определяется направлением вектора
определяется направлением вектора 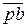 .
.
Согласно уравнению (1) вектор 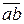 изображает относительную скорость
изображает относительную скорость 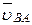 точки В во вращении вокруг точки А:
точки В во вращении вокруг точки А:
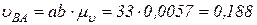 м/с.
м/с.
Согласно уравнению (2) вектор 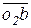 (
(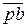 ) изображает относительную скорость
) изображает относительную скорость 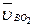 точки В во вращении вокруг точки O 2:
точки В во вращении вокруг точки O 2:
 м/с.
м/с.
 |
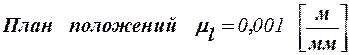
Рис. 5.2
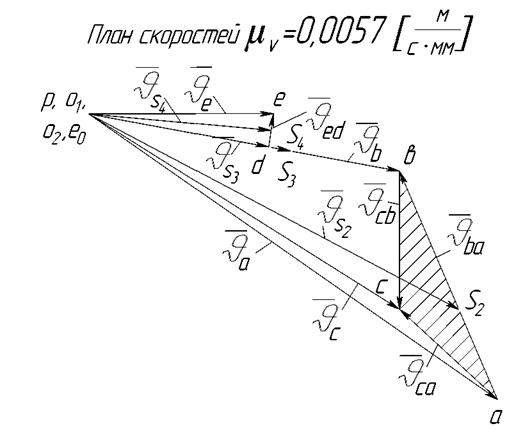 |
Рис. 5.3
 |
Рис. 5.4
Положение точки с (конец вектора скорости точки С) определяем на плане скоростей по теореме подобия (третье свойство планов скоростей). На отрезке ab плана скоростей строим треугольник аbс, подобный треугольнику ABC звена 2. Определяем длины отрезков ас и bc из пропорций
 и
и 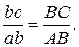
Поскольку АС = ВС, то
 мм.
мм.
Из точек а и b плана скоростей радиусами, равными соответственно отрезкам ас и bc, делаем засечки. Получив две точки пересечения этих дуг, справа и слева от вектора  . За точку с плана скоростей следует взять ту из полученных точек, при которой порядок букв в треугольниках abc и ABC будет одинаковым. Так, например, при обходе сторон
. За точку с плана скоростей следует взять ту из полученных точек, при которой порядок букв в треугольниках abc и ABC будет одинаковым. Так, например, при обходе сторон  ABC звена 2 по направлению вращения часовой стрелки читаем: А
ABC звена 2 по направлению вращения часовой стрелки читаем: А С
С  В. Порядок букв в треугольнике abc при обходе сторон треугольника также по часовой стрелке должен сохраниться а
В. Порядок букв в треугольнике abc при обходе сторон треугольника также по часовой стрелке должен сохраниться а  с
с  b. Следовательно, точка с плана скоростей будет слева от вектора
b. Следовательно, точка с плана скоростей будет слева от вектора  .
.
Соединяем полюс плана скоростей р с точкой с и определяем величину скорости  точки С:
точки С:
 м/с.
м/с.
Согласно тому же свойству планов скоростей находим положение точки d на плане исходя из пропорции:
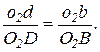
В этом случае фигура относительных скоростей o2db на плане скоростей будет прямой по подобию с прямой О2B механизма:
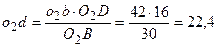 мм.
мм.
Определив положение точки d на плане скоростей, находим величину скорости точки D
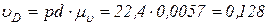 м/с.
м/с.
Скорость точки Е шатуна DE представляем в виде векторной суммы переносной и относительной скоростей. Для ееопределения воспользуемся векторными уравнениями:
 (3)
(3)
 (4)
(4)
где  — скорость точки D в переносном движении;
— скорость точки D в переносном движении;  — относительная скорость точки Е во вращении вокруг точки D;
— относительная скорость точки Е во вращении вокруг точки D; 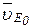 — скорость точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;
— скорость точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна; 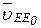 — скорость точки Е в поступательном движении относительно точки Е0.
— скорость точки Е в поступательном движении относительно точки Е0.
В этих уравнениях скорость  известна по величине и направлению, скорость
известна по величине и направлению, скорость 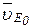 = 0. Относительные скорости
= 0. Относительные скорости  и
и 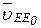 известны лишь по линиям действия:
известны лишь по линиям действия:  перпендикулярна к звену DE,
перпендикулярна к звену DE, 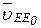 параллельна оси направляющих ползуна. Для определения скорости точки Е через точку d плана скоростей проводим перпендикулярно звену DE линию действия скорости
параллельна оси направляющих ползуна. Для определения скорости точки Е через точку d плана скоростей проводим перпендикулярно звену DE линию действия скорости  , а через точку е0, совпадающую с полюсом плана р параллельно оси направляющих ползуна (х — х) — линию действия скорости
, а через точку е0, совпадающую с полюсом плана р параллельно оси направляющих ползуна (х — х) — линию действия скорости 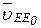 . Точка е пересечения этих линий действия определяет конец вектора скорости
. Точка е пересечения этих линий действия определяет конец вектора скорости  точки Е. Величина скорости
точки Е. Величина скорости
 м/с.
м/с.
Вектор de определяет величину и направление скорости
 м/с.
м/с.
Для определения скоростей центров масс звеньев пользуемся теоремой подобия (третье свойство планов скоростей): находим на плане точки s2, s3, s4, подобные центрам тяжести звеньев S2, S3 и S4. Из полюса р в эти точки проводим векторы. Определяем величины скоростей центров тяжести:
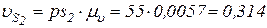 м/с;
м/с;
 м/с;
м/с;
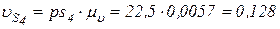 м/с.
м/с.
Переходим к определению угловых скоростей звеньев. Угловая скорость ω1 ведущего звена известна по величине и направлению (ω1 = 12,56 1/с и это звено вращается по часовой стрелке).
Чтобы определить угловую скорость ω2 звена АВ, рассмотрим вращение точки В вокруг точки А. Направление скорости 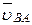 точки В во вращении вокруг точки А определяется направлением вектора
точки В во вращении вокруг точки А определяется направлением вектора 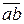 . Мысленно переносим этот вектор в точку В механизма и считаем точку А как бы неподвижной. Точка В в направлении вектора
. Мысленно переносим этот вектор в точку В механизма и считаем точку А как бы неподвижной. Точка В в направлении вектора 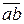 вращается относительно точки А против часовой стрелки, что и определяет направление вращения звена АВ. Находим величину угловой скорости второго звена по формуле
вращается относительно точки А против часовой стрелки, что и определяет направление вращения звена АВ. Находим величину угловой скорости второго звена по формуле
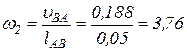 1/c.
1/c.
При определении направления угловой скорости ω3 поступаем аналогично. Перенесенный в точку В звена O 2 В вектор 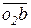 показывает, что точка В вращается относительно точки O 2 по часовой стрелке. Это определяет направление угловой скорости третьего звена
показывает, что точка В вращается относительно точки O 2 по часовой стрелке. Это определяет направление угловой скорости третьего звена
 1/с.
1/с.
Чтобы определить угловую скорость ω4 звена DE, мысленно переносим вектор 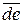 скорости
скорости  в точку Е. В направлении вектора
в точку Е. В направлении вектора 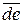 точка Е вращается относительно точки D, которую считаем как бы неподвижной, против часовой стрелки, что и определяет направление вращения звена DE. Величина этой угловой скорости
точка Е вращается относительно точки D, которую считаем как бы неподвижной, против часовой стрелки, что и определяет направление вращения звена DE. Величина этой угловой скорости
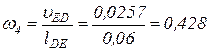 1/с.
1/с.
Угловая скорость ползуна 5, совершающего прямолинейное поступательное движение, равна нулю.
План ускорений. По аналогии с планами скоростей при помощи планов ускорений можно найти ускорения любых точек механизма. При построении планов ускорений также следует пользоваться их изображающими свойствами, заключающимися в следующем:
1. Векторы, исходящие из полюса, изображают абсолютные ускорения соответствующих точек механизма в масштабе плана ускорений. Точки плана ускорений, соответствующие точкам, ускорения которых равны нулю, располагаются в полюсе.
2. Векторы, соединяющие концы векторов абсолютных ускорений, выражают в том же масштабе полные относительные ускорения.
3. Полные относительные ускорения на плане ускорений образуют фигуру, подобную одноименной жесткой фигуре на плане положения механизма, но повернутую по отношению к последней на некоторый угол 180° — 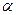 в сторону мгновенного углового ускорения данного звена, где
в сторону мгновенного углового ускорения данного звена, где
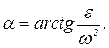
Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то обычно концы векторов абсолютных ускорений на планах ускорений обозначают буквами, соответствующими названию точек. Концы векторов нормальных составляющих ускорения обозначают другими буквами, не встречающимися в обозначениях точек механизма.
Пример Методом планов ускорений определить абсолютные и относительные ускорения точек звеньев и угловые ускорения звеньев механизма (рис. 5.2 ).
Решение. Определим ускорение точки А. Поскольку звено O 1 A вращается равномерно  где
где 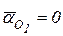 и
и 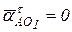 , то точка А имеет только нормальное ускорение, которое направлено по звену O 1 A к центру вращения. Величина этого ускорения:
, то точка А имеет только нормальное ускорение, которое направлено по звену O 1 A к центру вращения. Величина этого ускорения:
 м/с
м/с .
.
Выбираем длину отрезка р'а', изображающего вектор ускорения  точки А, тогда масштаб плана ускорений
точки А, тогда масштаб плана ускорений
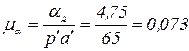 м/с
м/с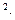 мм.
мм.
Из произвольной точки р', принятой за полюс плана ускорений, откладываем параллельно звену О 1 А в направлении от точки А к точке О 1 отрезок р'а' (рис. 5.4).
Ускорения точек О 1 и O 2 механизма равны нулю, следовательно, точки о' 1 и о 2 будут совпадать с полюсом плана ускорений.
Рассматриваем движение точки В со звеньями АВ и BO 2 и по аналогии с планом скоростей составляем векторные уравнения:
 (5)
(5)
 (6)
(6)
Полные относительные ускорения  и
и 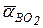 , представляем в виде суммы двух составляющих — нормальной, направленной по оси соответствующего звена к центру вращения в относительном движении, и тангенциальной, перпендикулярной к этому звену. Тогда уравнения (5) и (6) можно записать в следующем виде:
, представляем в виде суммы двух составляющих — нормальной, направленной по оси соответствующего звена к центру вращения в относительном движении, и тангенциальной, перпендикулярной к этому звену. Тогда уравнения (5) и (6) можно записать в следующем виде:
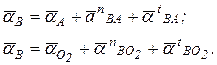
В этих уравнениях ускорение аА известно по величине и по направлению, ускорение  = 0.
= 0.
Определяем величины нормальных ускорений:
 м/с
м/с ;
;
 м/с
м/с .
.
Ускорение  направлено по оси звена АВ от точки В к точке А, ускорение
направлено по оси звена АВ от точки В к точке А, ускорение  — по оси звена O 2 В от точки В к точке O 2.
— по оси звена O 2 В от точки В к точке O 2.
Относительные тангенциальные ускорения известны только по линиям их действия. Ускорение  перпендикулярно звену АВ, а ускорение
перпендикулярно звену АВ, а ускорение  перпендикулярно звену O 2 В. Величины и направления тангенциальных ускорений определяем путем построения плана ускорений.
перпендикулярно звену O 2 В. Величины и направления тангенциальных ускорений определяем путем построения плана ускорений.
От точки а' плана ускорений параллельно звену АВ в направлении от точки В к точке А откладываем вектор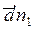 изображающий ускорение
изображающий ускорение  . Длина этого отрезка
. Длина этого отрезка
 мм.
мм.
Через точку п 1 проводим перпендикулярно к звену AB линию действия тангенциального ускорения  . Затем от точки о' 2 плана ускорений, совпадающей с полюсом р', параллельно звену O 2 В в направлении от точки В к точке O 2 откладываем вектор
. Затем от точки о' 2 плана ускорений, совпадающей с полюсом р', параллельно звену O 2 В в направлении от точки В к точке O 2 откладываем вектор 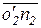 , изображающий ускорение
, изображающий ускорение  . Определим длину этого отрезка:
. Определим длину этого отрезка:
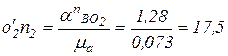 мм.
мм.
Через точку п 2 проводим перпендикулярно звену O 2 В линию действия тангенциального ускорения  . На пересечении линий действия ускорений
. На пересечении линий действия ускорений 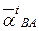 и
и  получим точку b — конец вектора р'b', изображающего ускорение
получим точку b — конец вектора р'b', изображающего ускорение 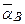 точки В механизма:
точки В механизма:
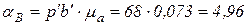 м/с
м/с .
.
Точка b' определяет также концы векторов 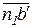 и
и  тангенциальных ускорений
тангенциальных ускорений 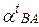 и
и  :
:
 м/с
м/с ;
;
 м/с
м/с .
.
Вектор  изображает полное относительное ускорение
изображает полное относительное ускорение 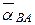 точки В во вращении вокруг точки А:
точки В во вращении вокруг точки А:
 м/с
м/с .
.
Вектор  полного ускорения
полного ускорения 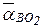 точки В во вращении относительно точки O 2 механизма совпадает с вектором
точки В во вращении относительно точки O 2 механизма совпадает с вектором  абсолютного ускорения точки В. Следовательно:
абсолютного ускорения точки В. Следовательно:
 м/с
м/с .
.
Исходя из третьего свойства планов ускорений  а'b'с' - относительных ускорений должен быть подобен
а'b'с' - относительных ускорений должен быть подобен  ABC звена 2, т. е. можно составить пропорции
ABC звена 2, т. е. можно составить пропорции
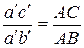 и
и  .
.
Поскольку АС =ВС, то
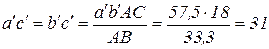 мм.
мм.
Из точек а' и b' плана ускорений радиусами, равными соответственно длинам отрезков а'с' и b'с', делаем засечки. Из полученных точек пересечения засекающих дуг (слева и справа от вектора 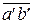 ) в качестве точки с' выбираем точку, расположенную слева, так как при этом порядок букв при обходе треугольника а'b'с' плана ускорений и треугольника ABC механизма будет одинаковым. Соединив полюс плана ускорений с точкой с', получаем вектор абсолютного ускорения точки С механизма:
) в качестве точки с' выбираем точку, расположенную слева, так как при этом порядок букв при обходе треугольника а'b'с' плана ускорений и треугольника ABC механизма будет одинаковым. Соединив полюс плана ускорений с точкой с', получаем вектор абсолютного ускорения точки С механизма:
 м/с
м/с
Находим положение точки d' на плане ускорений исходя из пропорции
откуда 

Следовательно, абсолютное ускорение точки D
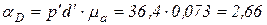 м/с
м/с .
.
Для определения ускорения точки Е воспользуемся векторными уравнениями:
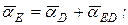 (7)
(7)
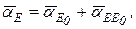 (8)
(8)
где  — абсолютное ускорение точки D;
— абсолютное ускорение точки D;  — полное относительное ускорение точки Е во вращении вокруг точки D;
— полное относительное ускорение точки Е во вращении вокруг точки D;  — ускорение точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна;
— ускорение точки Е0, принадлежащей стойке и совпадающей в данный момент с точкой Е ползуна; 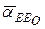 — ускорение точки Е в поступательном движении относительно точки E0. В этих уравнениях:
— ускорение точки Е в поступательном движении относительно точки E0. В этих уравнениях:
а) ускорение  известно по величине и по направлению;
известно по величине и по направлению;
б) полное относительное ускорение  представляем состоящим из нормальной
представляем состоящим из нормальной 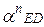 и тангенциальной
и тангенциальной 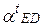 составляющих, тогда уравнение (8) принимает вид:
составляющих, тогда уравнение (8) принимает вид:

где нормальное ускорение
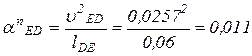 м/с
м/с
направлено по оси звена DE от точки Е к точке D.
Для тангенциального ускорения  известна только линия его действия, перпендикулярная к звену DE;
известна только линия его действия, перпендикулярная к звену DE;
в) ускорение  = 0;
= 0;
г) ускорение 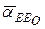 известно по линии действия; оно направлено параллельно оси направляющих ползуна.
известно по линии действия; оно направлено параллельно оси направляющих ползуна.
От точки d' плана ускорений параллельно звену DE в направлении от точки Е к точке D откладываем вектор 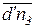 , изображающий нормальное ускорение
, изображающий нормальное ускорение 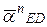 , предварительно определив длину этого отрезка:
, предварительно определив длину этого отрезка:
 мм.
мм.
Поскольку его длина 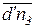 в выбранном масштабе плана ускорений не превышает 1 мм, то точки п 3 и d' на плане совпадают.
в выбранном масштабе плана ускорений не превышает 1 мм, то точки п 3 и d' на плане совпадают.
Из точки п 3 перпендикулярно звену DE проводим линию действия тангенциального ускорения  . Поскольку ускорение
. Поскольку ускорение  равно нулю, то точка е'0 на плане ускорений совпадает с полюсом р'. Через точку е'0 параллельно оси направляющих ползуна х — х проводим линию действия ускорения
равно нулю, то точка е'0 на плане ускорений совпадает с полюсом р'. Через точку е'0 параллельно оси направляющих ползуна х — х проводим линию действия ускорения 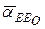 . Точка е' пересечения этих линий действия определяет конец вектора, изображающего абсолютное ускорение точки Е:
. Точка е' пересечения этих линий действия определяет конец вектора, изображающего абсолютное ускорение точки Е:
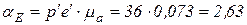 м/с
м/с .
.
Точка е' определяет также концы векторов 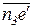 =
= 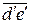 , изображающих тангенциальное
, изображающих тангенциальное  и полное относительное
и полное относительное  ускорения:
ускорения:
 м/с
м/с .
.
Вектор 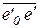 ускорения
ускорения 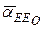 совпадает с вектором
совпадает с вектором  абсолютного ускорения точки Е. Следовательно,
абсолютного ускорения точки Е. Следовательно,
 м/с
м/с .
.
Зная положения центров тяжести S2, S3, S4 на звеньях по аналогии с планом скоростей находим по правилу подобия соответствующие им точки 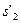 ,
,  ,
,  на плане ускорений. Соединяем полученные точки с полюсом плана ускорений и определяем ускорения центров тяжести:
на плане ускорений. Соединяем полученные точки с полюсом плана ускорений и определяем ускорения центров тяжести:
 м/с
м/с ;
;
 м/с
м/с ;
;
 м/с
м/с .
.
Определяем угловые ускорения звеньев. Угловое ускорение  ведущего звена О1А, совершающего равномерное движение, равно нулю.
ведущего звена О1А, совершающего равномерное движение, равно нулю.
Угловое ускорение звена 2
 1/c
1/c .
.
Для определения направления углового ускорения 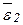 звена 2 рассмотрим вращение точки В вокруг точки А. Перенесем мысленно вектор
звена 2 рассмотрим вращение точки В вокруг точки А. Перенесем мысленно вектор 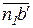 тангенциального ускорения
тангенциального ускорения 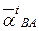 в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки, что и определяет направление углового ускорения
в точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки, что и определяет направление углового ускорения  2.
2.
Угловое ускорение  звена О2B направлено против часовой стрелки (по вращению точки В относительно точки O2 в направлении вектора
звена О2B направлено против часовой стрелки (по вращению точки В относительно точки O2 в направлении вектора 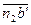 тангенциального ускорения
тангенциального ускорения  ). Величина его определяется по формуле:
). Величина его определяется по формуле:
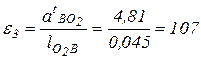 1/c
1/c .
.
Угловое ускорение  звена DE направлено в соответствии с круговой стрелкой, направленной против часовой стрелки (по вращению точки Е относительно точки D в направлении вектора
звена DE направлено в соответствии с круговой стрелкой, направленной против часовой стрелки (по вращению точки Е относительно точки D в направлении вектора 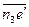 тангенциального ускорения
тангенциального ускорения  и определяется по формуле
и определяется по формуле
 1/c
1/c .
.
Звено 5 совершает поступательное движение, поэтому угловое ускорение 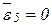 ; ускорение его центра тяжести
; ускорение его центра тяжести 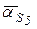 , совпадает по величине и направлению с ускорением
, совпадает по величине и направлению с ускорением 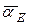 точки Е.
точки Е.
Контрольные вопросы по теме «Кинематический анализ механизмов»
1. Что называется "функцией положения" для звена или точки механизма?
2. Какие функции называются кинематическими характеристиками механизма?
3. Какие функции называются кинематическими передаточными функциями механизма?
4. Какие передаточные функции механизма называются главными, а какие вспомогательными?
5. Перечислите методы кинематического исследования механизмов.
6. Напишите формулы, устанавливающие связь между передаточными функциями и кинематическими характеристиками механизма.
8. Что называется циклом?
9. Сформулируйте теорему о сложении движения.
10. Запишите векторные уравнения для определения скорости, ускорения точки звена механизма.
11. Сформулируйте свойства планов скоростей и ускорений.
12. Как определить скорость или ускорение какой-либо точки, лежащей на звене механизма.
13. Как определяется угловая скорость звена механизма по величине и по направлению?
14. Как определяется механизма угловое ускорение звена механизма по величине и по направлению?
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1119; Нарушение авторских прав?; Мы поможем в написании вашей работы!