Матрицы и операции над ними

Тема I. ЛИНЕЙНАЯ АЛГЕБРА

Передачи ключей, печатей или пломбиров и содержимого сейфа

ЖУРНАЛ

Отделения больницы

Предметно-количественного учета наркотических средств

ЖУРНАЛ

(психотропных веществ) процедурной (дежурной) медицинской сестрой

Наименование средства___________________________

Единица измерения ______________________________

№ п/п	Среднесуточная потребность в наркотических средствах и психотропных веществах по отделению	Дата	Приход
от кого получено	количество	фамилия, инициалы, подпись процедурной медсестры отделения

Расход	Остаток
фамилия, инициалы больного, получившего наркотические средства (психотропные вещества), номер истории болезни	количество израсходованного наркотического средства (психотропные вещества)	фамилия, инициалы, подпись медсестры, производившей выдачу (введение) наркотических средств (психотропных веществ)	подпись старшей медсестры

Таблица 2

Наименование организации ____________________

(металлического шкафа, холодильника)

Дата	Наименование наркотических средств и психотропных веществ/количество использованных ампул (флаконов) из-под наркотических средств и психотропных веществ	Фамилия, инициалы, подпись сдавшего	Фамилия, инициалы, подпись принявшего

Определение 1.1. Матрицей размерности 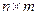называется прямоугольная таблица чисел, состоящая из 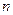строк и 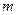столбцов. Числа, составляющие таблицу, называются элементами матрицы.

Для обозначения матриц используют заглавные буквы латинского алфавита: А, В, С, …; для обозначения элементов – строчные буквы с двойной индексацией: 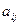, где i – номер строки, в которой находится элемент, j – номер столбца

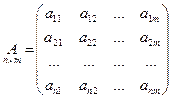
или, в сокращённой записи, .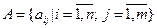

Пример 1.1. Матрица , элементы 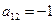и .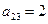

Замечание. Наряду с круглыми скобками для обозначения матриц используются также и другие символы: [ ], || ||.

Виды матриц.

Определение 1.2. Матрица размерности 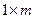называется матрицей – строкой (вектором – строкой), а 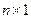- матрицей – столбцом (вектором – столбцом).

Определение 1.3. Матрица называется нулевой, если все её элементы равны нулю.

Определение 1.4. Матрица называется квадратной, если число строк совпадает с числом столбцов (n=m). Число n называется порядком матрицы.

Определение 1.5. Элементы квадратной матрицы, у которых i=j: a₁₁, a₂₂,…,a_nn, называются диагональными и образуют главную диагональ матрицы.

Определение 1.6. Квадратная матрица, у которой все элементы, расположенные под (над) главной диагональю, равны нулю, называется верхней (нижней) треугольной.

Определение 1.7. Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной.

Определение 1.8. Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной и обозначается Е.

проиллюстрировать определения 1.2 – 1.8 на примерах

Действия над матрицами.

1) Сравнение матриц.

Матрицы одинаковой размерности равны между собой, если равны их соответствующие элементы: = .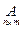

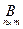
2) Умножение матрицы на число.

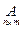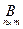Произведением матрицы на число будет матрица , элементы которой вычисляются по правилу .

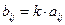Следствие. Общий множитель всех элементов можно выносить за знак матрицы.

3) Сложение (вычитание) матриц.

Суммой (разностью) двух матриц одинаковой размерности 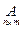и будет матрица 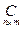, элементы которой вычисляются по правилу .

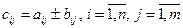Пример 1.2. Даны матрицы 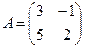, 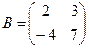. Найти матрицу .

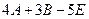Решение. 1) 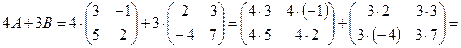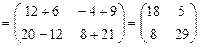; 2) .

Определение 1.9. Две матрицы называются согласованными, если количество столбцов в первой матрице равно количеству строк во второй.

4) Умножение матриц.

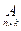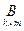Произведением двух согласованных матриц и будет матрица 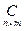, элементы которой вычисляются по правилу 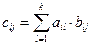, то есть являются скалярным произведением 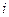– ой строки первой матрицы на 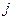– ый столбец второй.

Пример 1.3. Даны матрицы 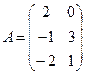, 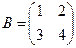. Найти матрицу .

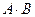Решение. Матрицы являются согласованными (2=2), поэтому их произведение существует. Это будет матрица С размерностью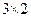

С==.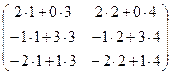

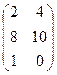Замечание. Умножение матриц имеет ряд характерных особенностей:

а) Из существования произведения 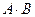не следует существование произведения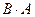

(смотри пример 1.3);

б) Если существуют матрицы 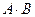и 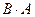, то их размерности могут не совпадать. Пусть,

например, 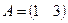, , 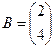тогда 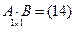и ;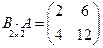

в) Если существуют матрицы одинаковой размерност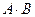и и 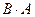, то не обязательно

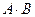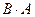=. Показать самостоятельно для матриц 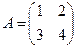и .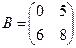

г) Произведение двух ненулевых матриц может равняться нулю

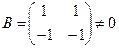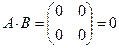, , (проверить самостоятельно);

5) Возведение матрицы в степень.

Натуральной степенью 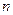квадратной матрицы называется произведение 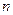матриц,

равных : . Кроме того, определим, что 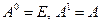. Заметим, что из

уравнения 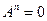не следует, что 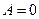. Так, например, 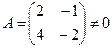, однако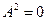

(проверить самостоятельно).

6) Транспонирование матриц.

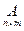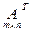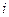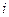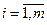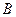Транспонированной матрицей к матрице называется матрица , - я строка которой совпадает с - м столбцом матрицы (). Свойства транспонирования: пусть и - матрицы, - число, тогда ; ; ; .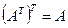

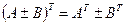Пример 1.4. Даны матрицы 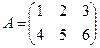, 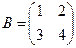. Найти матрицу .

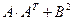Решение. 1) ;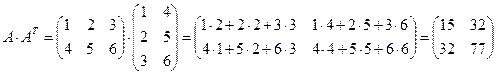

2) 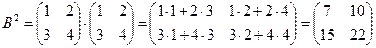; 3) +=

.

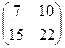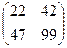Дата добавления: 2014-01-11