
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обратная матрица. Вспомнить понятия противоположных и обратных чисел
|
|
|
|
Вспомнить понятия противоположных и обратных чисел
Пусть  - квадратная матрица порядка
- квадратная матрица порядка 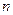 .
.
Определение 1.13. Матрица  называется обратной к матрице
называется обратной к матрице  , если имеет место равенство
, если имеет место равенство
 .
.
Из определения следует, что  также является квадратной порядка
также является квадратной порядка 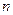 .
.
Замечание. Понятие обратной матрицы вводится только для квадратных матриц, однако не для каждой квадратной матрицы существует обратная. Приведём критерий существования обратной матрицы.
Определение 1.14. Матрица  называется невырожденной, если её определитель отличен от нуля (
называется невырожденной, если её определитель отличен от нуля ( ). В противном случае матрица
). В противном случае матрица  называется вырожденной.
называется вырожденной.
Определение 1.15. Матрица  , состоящая из алгебраических дополнений к элементам матрицы
, состоящая из алгебраических дополнений к элементам матрицы 
 , называется союзной (или присоединённой) к
, называется союзной (или присоединённой) к  .
.
Теорема 1.1. Для существования у матрицы  обратной матрицы необходимо и достаточно, чтобы матрица
обратной матрицы необходимо и достаточно, чтобы матрица  была невырожденной.
была невырожденной.
Доказательство. Необходимость (известно, что существует матрица, обратная к  ; надо показать, что определитель
; надо показать, что определитель  отличен от нуля). По определению обратной матрицы
отличен от нуля). По определению обратной матрицы  . По свойству 7 определителей
. По свойству 7 определителей  , следовательно каждый из определителей
, следовательно каждый из определителей  и
и  отличен от нуля.
отличен от нуля.
Достаточность (известно, что определитель  отличен от нуля; надо показать, что существует матрица, обратная к
отличен от нуля; надо показать, что существует матрица, обратная к  ) Рассмотрим матрицу
) Рассмотрим матрицу 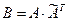 . По следствию из свойства 6 определителей
. По следствию из свойства 6 определителей 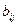 =
=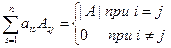 , следовательно
, следовательно 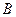 - диагональная матрица вида
- диагональная матрица вида

и, кроме того, 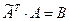 . Таким образом, матрица
. Таким образом, матрица  является обратной к матрице
является обратной к матрице  , поскольку
, поскольку 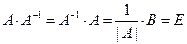 .
.
Замечание. Из доказательства теоремы вытекает схема нахождения матрицы, обратной к матрице  : 1) вычислить
: 1) вычислить  и убедится, что он отличен от нуля (в противном случае обратной матрицы не существует); 2) найти союзную матрицу
и убедится, что он отличен от нуля (в противном случае обратной матрицы не существует); 2) найти союзную матрицу  (матрицу из алгебраических дополнений; 3) записать матрицу
(матрицу из алгебраических дополнений; 3) записать матрицу  , пользуясь формулой
, пользуясь формулой  ; 4) сделать проверку, подставив полученное значение
; 4) сделать проверку, подставив полученное значение  в соотношение
в соотношение  (определение обратной матрицы).
(определение обратной матрицы).
Пример 1.7. Пусть  .Найти
.Найти  .
.
Решение. 1)  (смотри пример 1.6), следовательно, обратная матрица существует; 2)
(смотри пример 1.6), следовательно, обратная матрица существует; 2) 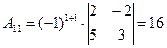 ;
;  ;
; 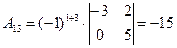 ;
;
 ;
;  ;
;  ;
;
 ;
;  ;
; 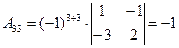 ;
;
Таким образом,  =
=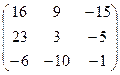 ,
,  и, следовательно,
и, следовательно,
3)  =
=
 . Проверку выполнить самостоятельно!
. Проверку выполнить самостоятельно!
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 461; Нарушение авторских прав?; Мы поможем в написании вашей работы!