Понятие ветви многозначной функции

Если функция 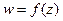осуществляет взаимно однозначное отображение области E на область G, то она называется однолистной. Однолистная функция имеет обратную 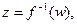которая отображает область G на E.

Можно доказать, что если однолистная функция 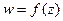аналитическая в E, то обратная функция является аналитической в области G. При этом производная обратной функции в нуль не обращается и имеет место обычная формула

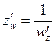(1)

(см. (6¢) §1 гл. 3 ч.I). Например, линейная функция 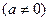является однолистной во всей комплексной плоскости z, имеет обратную функцию 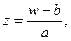причем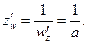

Однако функция как это видно из §1, на всей комплексной плоскости однолистной не будет,, но можно найти множество областей комплексной плоскости z, в которых она однолистна, например, в каждом из секторов

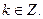(2)

В каждом из этих секторов она имеет обратную функцию 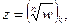которая отображает k-й лист поверхности Римана на соответствующий сектор (2). Эти обратные функции называют ветвями многозначной функции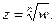

Чтобы зафиксировать ветвь, достаточно указать номер листа поверхности Римана или номер сектора, в который она отображает этот лист, или указать значение функции в одной из точек области определения.

Будем теперь, как обычно, независимое переменное обозначать буквой z, а функцию буквой w. Рассмотрим многозначную функцию 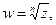заданную во всей комплексной плоскости z с разрезом по положительной полуоси. Зафиксируем ветвь этой функции, положив, например, при 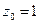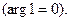Эта ветвь взаимно однозначно отобразит указанную плоскость z на сектор 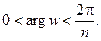Если сделать разрез плоскости z вдоль отрицательной полуоси, то эта же ветвь отобразит данную плоскость на сектор А если никакого разреза не делать, то появится возможность точке z сделать полный оборот вокруг начала координат. 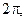Тогда получит приращение а выбранная ветвь перейдет в другую, т.е. перестанет быть однозначной функцией. Действительно, после полного оборота точка 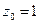будет иметь аргумент равный 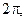а

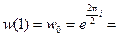
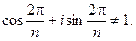
Отсюда ясно, что в области, содержащей точку нельзя выделить однозначную ветвь многозначной функции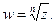

Точка, обладающая тем свойством, что оборот вокруг нее переводит одну ветвь многозначной функции в другую, называется особой точкой (точкой ветвления). Очевидно, для функции 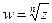точкой ветвления является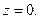

Комплексная плоскость с присоединенной бесконечно удаленной точкой 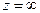называется расширенной комплексной плоскостью. В расширенной комплексной плоскости функция 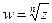имеет еще одну точку ветвления, а именно .

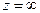Можно убедиться, что эти же точки и 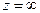являются точками ветвления и для многозначной функции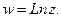

Рассмотрим функцию 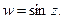Поскольку она периодическая, то не может быть однолистной во всей комплексной плоскости. Однако, например, в каждой из полос

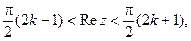
(3)

она однолистная и, следовательно, имеет обратную аналитическую функцию

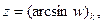
ветвь многозначной функции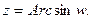

Согласно (7) §2

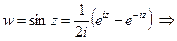
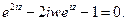
Решая это уравнение относительно получим

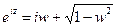
или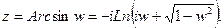

Переобозначая переменные, запишем

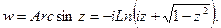(4)

Аналогично можно доказать, что

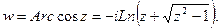(5)

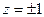Точки и 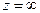расширенной комплексной плоскости являются точками ветвления для функци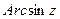й и Однозначные аналитические ветви этих функций можно выделить, например, в плоскости с разрезами на действительной ос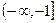и и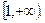

Дата добавления: 2014-01-11