
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрический смысл производной
|
|
|
|

|
Пусть функция 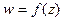 отображает некоторую окрестность точки
отображает некоторую окрестность точки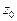 в окрестность точки
в окрестность точки  и всякую дугу
и всякую дугу 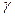 в дугу Г.
в дугу Г.
Пусть 
 (1)
(1)
Из (1) следуют равенства (см. (6) §1)
 (2)
(2)
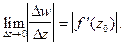 (3)
(3)
Запишем равенство (2) в виде
 (2')
(2')
и дадим его геометрическую интерпритацию. это угол наклона секущей, проходящей через точки
это угол наклона секущей, проходящей через точки 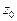 и
и 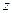 , а
, а 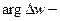 угол наклона секущей, проходящей через точки
угол наклона секущей, проходящей через точки  и
и 
 Т.к. предельное положение секущей есть касательная, то
Т.к. предельное положение секущей есть касательная, то  можно переписать так:
можно переписать так:
 (4)
(4)
где  и
и  углы наклона соответствующих касательных (см. рис. 6). Из (4) ясен геометрический смысл аргумента производной. Это угол поворота касательной при отображении
углы наклона соответствующих касательных (см. рис. 6). Из (4) ясен геометрический смысл аргумента производной. Это угол поворота касательной при отображении 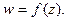 Поскольку производная не зависит от того, по какой кривой z стремится к
Поскольку производная не зависит от того, по какой кривой z стремится к 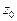 , то ясно, что все бесконечно малые дуги, выходящие из точки
, то ясно, что все бесконечно малые дуги, выходящие из точки 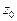 , при отображении функций
, при отображении функций  поворачиваются на один и тот же угол
поворачиваются на один и тот же угол  если
если 
Следствие. Угол между кривыми, проходящими через точку 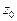 , при отображении аналитической функцией
, при отображении аналитической функцией  не изменяется, если
не изменяется, если  Это свойство данного отображения называют свойством сохранения углов.
Это свойство данного отображения называют свойством сохранения углов.
Рассмотрим геометрический смысл равенства (3). Модули разности  и
и  есть расстояния между точками
есть расстояния между точками 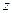 и
и 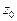 ,
,  и
и  соответственно. Поэтому
соответственно. Поэтому  коэффициент растяжения (сжатия) бесконечно малой дуги в точке
коэффициент растяжения (сжатия) бесконечно малой дуги в точке 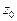 при отображении функцией
при отображении функцией 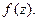 Коэффициент растяжения не зависит от направления дуги, поэтому это свойство данного отображения называют свойством постоянства растяжения.
Коэффициент растяжения не зависит от направления дуги, поэтому это свойство данного отображения называют свойством постоянства растяжения.
Отображение, осуществляемое аналитической функцией, называют конформным в точке, в которой производная отлична от нуля. Если  в каждой точке области
в каждой точке области  то аналитическая функция
то аналитическая функция  осуществляет конформное отображение области
осуществляет конформное отображение области  на область
на область 
Пример. Рассмотрим отображение  Производная
Производная  обращается в нуль только в точках
обращается в нуль только в точках  следовательно, отображение конформно всюду, исключая точки
следовательно, отображение конформно всюду, исключая точки 
 это означает, что бесконечно малые дуги, проходящие через точку
это означает, что бесконечно малые дуги, проходящие через точку  при отображении функцией
при отображении функцией  поворачиваются на угол
поворачиваются на угол  и растягиваются в шесть раз.
и растягиваются в шесть раз.
Если взять в плоскости z бесконечно малый треугольник, одна из вершин которого совпадает с точкой z0, то при отображении аналитической функцией 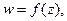
 в плоскости w ему будет соответствовать криволинейный треугольник с вершиной в точке
в плоскости w ему будет соответствовать криволинейный треугольник с вершиной в точке  Соответственные углы этих треугольников будут равны в силу свойства сохранения углов, а отношения соответственных сторон с точностью до бесконечно малых будут равны коэффициенту растяжения в точке z0. Такие треугольники называют подобными. Отсюда и название конформное отображение, т. е. cохраняющее форму.
Соответственные углы этих треугольников будут равны в силу свойства сохранения углов, а отношения соответственных сторон с точностью до бесконечно малых будут равны коэффициенту растяжения в точке z0. Такие треугольники называют подобными. Отсюда и название конформное отображение, т. е. cохраняющее форму.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 436; Нарушение авторских прав?; Мы поможем в написании вашей работы!