
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квантовая теория свободных электронов в металле
|
|
|
|
Рассмотрим поведение так называемых электронов в металле без учета влияния кристаллической решетки металла. Может возникнуть вполне уместный вопрос – как это «без учета влияния кристаллической решетки»? Обладающий небольшой энергией электрон должен с огромной трудом протискиваться через кристалл. Расстояние между атомами порядка нескольких ангстрем (1 ангстрем равен 10-10 м или 10 нм). Эффективный диаметр атомов при рассеянии на них порядка одного ангстрема. Следовательно, средний свободный пробег электрона между столкновениями будет порядка нескольких ангстрем (это почти ноль!), и электрон почти тотчас же должен влететь в какой-нибудь атом.
Однако опыт показывает, что электрон проходит через кристалл совершенно свободно, почти как в вакууме. Это явление объясняется чисто квантовым эффектом. Наличие неидеальностей в решетке (примесные атомы, вакансии, дислокации, тепловые колебания решетки и т.д.) приводят к тому, что металлы обладают сопротивлением.
Рассмотрим квантовое поведение свободных электронов в металле. Возьмем кубик металла со стороной L. Его объем V = L 3. Запустим вначале в кубик только один электрон. Потенциальную энергию этого электрона можно принять равной нулю (U = 0).
Рассмотрим стационарное уравнение Шредингера
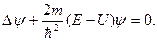 (1)
(1)
В декартовой системе координат при U = 0 оно примет вид
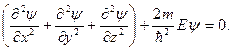 (2)
(2)
Введем обозначение  Параметр k имеет смысл волнового вектора, связанного с импульсом соотношением
Параметр k имеет смысл волнового вектора, связанного с импульсом соотношением  Тогда решение уравнения Шредингера можно записать в виде
Тогда решение уравнения Шредингера можно записать в виде
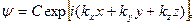 (3)
(3)
где i – мнимая единица, С – некоторая константа, определяемая из условий нормировки.
Так как мы не рассматриваем поведение электрона вне кубика, то потребуем выполнения для волновой функции условий периодичности (формально это означает, что мы рассматриваем бесконечное множество составленных вплотную друг к другу кубиков):
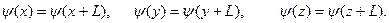 (4)
(4)
Эти условия будут выполнены только в том случае, если волновое число k принимает следующие значения:
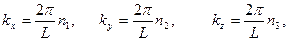 (5)
(5)
где n 1, n 2, n 3 – целые числа 0, 1, 2, 3, …, не равные нулю одновременно.
Чтобы это проверить, воспользуемся формулой Эйлера и условиями периодичности:
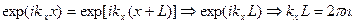 (6)
(6)
Таким образом, мы доказали, что значения волнового вектора и соответственно энергии квантуются. И для энергии получаем выражение
 (7)
(7)
Состояние электрона в металле будем определять значением волнового вектора 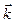 и спином. Так как значение волнового вектора определяется набором { n 1, n 2, n 3}, то, задавая набор { n 1, n 2, n 3}, мы тем самым определяем состояние электрона.
и спином. Так как значение волнового вектора определяется набором { n 1, n 2, n 3}, то, задавая набор { n 1, n 2, n 3}, мы тем самым определяем состояние электрона.
Для наглядного обозначения состояний электрона введем воображаемое пространство, по осям которого будем откладывать значения чисел { n 1, n 2, n 3} (рис. 5.1).
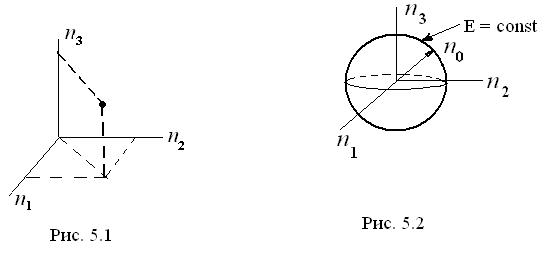
Тогда каждое состояние отобразится точкой в этом пространстве. Плотность размещения точек в этом пространстве равна единице (так как в каждом единичном кубике находится только одна точка и Δ n = 1). Поверхность равных значений энергии – сфера с радиусом
 (рис.5.2).
(рис.5.2).
Найдем число разрешенных состояний, располагающихся внутри этой сферы (число состояний, энергия которых не превышает Е). Обозначим его υ E. Так как плотность размещения точек равна единице, то это число равно просто объему этой сферы, умноженному на два (в каждом состоянии могут находиться по два электрона, обладающих спинами разного направления):
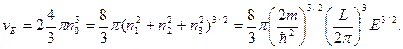 (8)
(8)
Учитывая, что L 3 равно объему кубика V, получаем окончательно
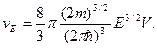 (9)
(9)
Запустим теперь в кубик много электронов (порядка числа атомов). В силу запрета Паули электроны разбегутся по разным состояниям. Эти состояния окажутся затем либо заняты электронами, либо свободными. Т.е. каждому электрону в этом пространстве квантовых чисел отводится своя маленькая «комнатка», которую он может и не занимать.
Посмотрим, что будет при абсолютном нуле температуры. Вследствие принципа Паули электроны будут занимать каждый свое место на самых нижних уровнях энергии. Поэтому все состояния с энергией, меньшей некоторого значения, будут заполнены электронами, а состояния с энергией, большей этого значения, будут свободны. Это значение энергии обозначается EF (0) и называется уровнем Ферми при абсолютном нуле температуры. Иначе можно сказать, что EF (0) – это максимальное значение энергии электронов при абсолютном нуле температуры. Его значение можно найти из условия, что число заполненных состояний при нулевой температуре должно быть равно числу всех электронов в металле:
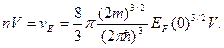 (10)
(10)
Откуда получаем
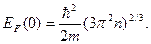 (11)
(11)
Здесь n – концентрация электронов в металле.
Оценим величину энергии Ферми EF (0). Возьмем для концентрации электронов среднее значение 5·1022 в одном см3. Тогда EF (0) будет около 5 эВ. Много это или мало? Чтобы сообщить классическому электронному газу такую энергию, его необходимо нагреть до температуры порядка 104 К (с учетом пропорциональности энергии и температуры). Средняя тепловая энергия при комнатной температуре составляет значение около 1/40 эВ. Такая энергия может возбудить только электроны, находящихся на самых верхних уровнях вблизи уровня Ферми. А их очень мало. Основная масса электронов, находящихся на более глубоких уровнях, не способна поглощать энергию и изменять свое состояние.
5.2. Распределение Ферми – Дирака. Фермионы
При абсолютном нуле температуры в каждом состоянии с энергией E ≤ EF (0) находится один электрон, в состояниях с E > EF (0) электронов нет. Для характеристики вероятности заполнения электронами различных состояний при Т ≠ 0 введем функцию распределения электронов по состояниям
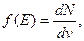 (12)
(12)
где dN – число электронов, находящихся в интервале состояний от v до v + dv; dv – число состояний с энергией, заключенной в интервале от Е до Е + dE. Число состояний dv = g (E) dE, где g (E) называется плотностью состояний и равно числу состояний, приходящихся на единичный интервал энергии. Для плотности состояний g (E) должно выполняться очевидное условие
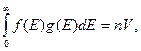 (13)
(13)
которое представляет собой по существу условие нормировки функции f (E).
Из определения f (E) следует, что она представляет вероятность того, что состояние с энергией Е занято электроном.

При абсолютном нуле температуры эта функция имеет вид: f (E) = 1 при Е ≤ ЕF (0) и f (E) = 0 при Е > ЕF (0) (рис. 5.3).
При повышении температуры функция f (E) деформируется – электроны вблизи ЕF (0) начинают занимать более высокие уровни энергии, внутренние же электроны не могут изменять состояние (рис. 5.4).
Определение вида функции распределения достаточно громоздко, поэтому его здесь приводим уже в законченном виде
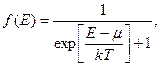 (14)
(14)
где f (E) – функция распределения Ферми – Дирака, μ – химический потенциал. Последний обозначают как ЕF (T) и называют просто уровень Ферми. При Т = 0 ЕF → ЕF (0). Учитывая новое обозначение уравнение (14) можно записать в виде
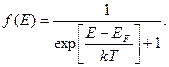 (15)
(15)
Частицы, подчиняющиеся распределению Ферми-Дирака, называются фермионы (электроны, нейтрино, нуклоны и т.д.). Это частицы с полуцелым спином. Для фермионов характерно то, что они никогда не занимают состояние, в котором уже что-то есть. Говорят, что фермионы не накапливаются в одном состоянии. Функции распределения Ферми – Дирака можно придать еще один смысл: это среднее число электронов, находящихся в состоянии с энергией Е. При Е = ЕF функция f (E) = 1/2, т.е. уровень Ферми – это уровень энергии, вероятность заполнения которого равна 1/2.
При больших значениях энергии, когда Е – ЕF >> kT, экспонента в (15) много больше единицы, и тогда распределение Ферми – Дирака переходит в классическое распределение Больцмана:
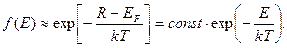 (16)
(16)
Поведение электронного газа существенно зависит от соотношения между температурой тела и температурой Ферми, равной 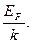 Различают два предельных случая:
Различают два предельных случая:
1. kT << EF. В этом случае газ электронов называется вырожденным.
2. kT >> EF. Такой газ называется невырожденным.
В металлах температура Ферми составляет величину порядка 104 K. Поэтому даже при температурах близких к плавлению электронный газ является вырожденным. В полупроводниках плотность свободных электронов гораздо ниже, чем в металлах, соответственно ниже значение температуры Ферми. Поэтому уже при комнатных температурах электронный газ во многих полупроводниках является невырожденным и подчиняется распределению Больцмана.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 3789; Нарушение авторских прав?; Мы поможем в написании вашей работы!