Квантовая теория теплоемкости кристаллов

Твердое тело можно рассматривать как систему большого числа N связанных частиц, совершающих нормальные гармонические колебания. В твердом теле возбуждаются тепловые колебания (фононы) с целым спектром частот ω_i. Полная энергия всех этих гармонических осцилляторов может быть записана в виде

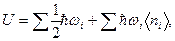(1)

где суммирование ведется по всем состояниям фононов в зоне Бриллюэна (в кубе со стороной 2π/ b, где b – постоянная решетки), а - среднее число фононов частоты ω_i, определяемое распределением Бозе – Эйнштейна при химическом потенциале μ = 0 (уравнение 25):

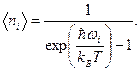(2)

Здесь k _Б – постоянная Больцмана.

В выражении для внутренней энергии можно опустить слагаемое 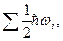представляющее энергию нулевых колебаний, поскольку она не зависит от температуры. С учетом выражения для среднего числа фононов значение энергии тела будет равно

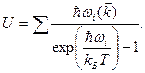(3)

Соответственно выражение для теплоемкости тела можно представить в виде

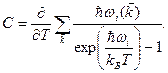(4) В выражениях (3) и (4) суммирование производится по всем значениям 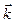внутри первой зоны Бриллюэна (например, для кубической решетки с постоянной решетки b зона Бриллюэна есть куб со сторонами 2π/ b). Частоты колебаний являются функцией волнового вектора 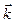. Температурная зависимость теплоемкости определяется только величиной 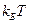в знаменателе экспоненты. Трудность расчета теплоемкости различных веществ по формуле (4) заключается в том, что мы не знаем истинного закона дисперсии 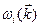для различных ветвей спектра фононов. Трудность можно преодолеть, рассматривая предельные случаи высоких и низких температур, а затем интерполировать полученные выражения на промежуточные температуры.

Случай высоких температур (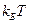>> ħ ω). Разлагая экспоненту, получаем

(5)

и выражение для молярной теплоемкости (4) переходит в

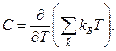(6)

Здесь под знаком суммы стоит величина, не зависящая от 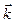, а суммирование проводится по всем волновым числам в пределах первой зоны Бриллюэна и всем ветвям спектра колебаний.

Для простоты рассмотрим простую кубическую кристаллографическую решетку. Тогда элементарная ячейка Браве содержит по одному атому с постоянной решетки b. В этом случае максимальное значение волнового числа в пределах первой зоны Бриллюэна будет равно π/6. Тогда число значений 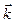соответствует в первой зоне Бриллюэна равно числу элементарных ячеек Браве, т.е. числу атомов в твердом теле N (для одного моля это N _A). Каждому значению 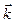соответствует три ветви спектра: одна продольная и две поперечные волны той же частоты. Тогда 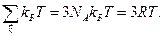(7)

Здесь R = N _A k _Б – универсальная газовая постоянная. Дифференцируя (7) по температуре, получаем

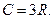(8)

Выражение (8) представляет собой закон Дюлонга и Пти, установленный опытным путем с довольно хорошим приближением для многих веществ при комнатных температурах.

Случай низких температур. В уравнениях (3) и (4) входит сумма функций по состояниям в первой зоне Бриллюэна. Следовательно, можно перейти от суммирования по этим состояниям к интегрированию в 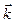- пространстве. Для этого рассмотрим твердое тело в виде кубика со стороной L и объемом V = L ³. В данном теле устанавливаются стоячие волны, максимальная длина волны которых λ = L. Им соответствуют состояния с минимальным значением волнового числа k_x вдоль оси Х

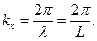(9)

Это значение можно принять за интервал изменения волнового числа 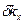, который много меньше значения волнового числа π/ b, соответствующего границе первой зоны Бриллюэна. Аналогичные соотношения можно написать и для направлений Y и Z.

Для наглядного представления состояний фононов введем воображаемое 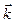- пространство, по осям которого будем откладывать значения k_{x ,} k_y, и k_z. Тогда каждое состояние фонона отобразится точкой в данном пространстве. В каждом элементе объема такого пространства

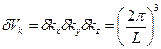(10)

находится только одна точка, отображающая состояние фонона. Тогда число состояний, располагающихся в произвольном элементе 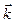- пространства 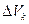будет равно отношению такого элемента к величине

.

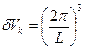Если в качестве такого элемента выбрать бесконечно маленький объем 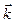- пространства

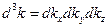, то число состояний в нем будет равно

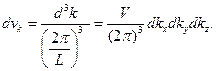(11)

Тогда сумму значений какой-либо функции 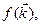зависящей от волнового вектора 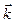, можно заменить на интеграл

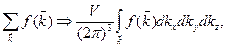(12)

где интеграл берется по всем значениям 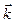, располагающимся в первой зоне Бриллюэна. Причем нужно помнить, что в общем случае зона Бриллюэна представляет достаточно сложную поверхность и в интеграл должны войти все точки 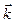- пространства, ограниченного зоной Бриллюэна.

При достаточно низких температурах, когда возбуждаются только состояния внутри зоны Бриллюэна, не примыкающие к ее границе, то в качестве бесконечно малого элемента 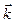- пространства можно взять тонкий сферический слой радиусом k и толщиной dk. Объем этого слоя 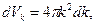и соответственно число состояний фононов dv_k, приходящихся на интервал значений от k до k + dk, будет равно

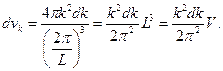(13)

С учетом замечания о трех ветвях спектра звуковых колебаний необходимо последнее выражение нужно помножить на три

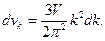(14)

Заменяя дискретный спектр волновых чисел на непрерывный, получаем

(15)

где интегрирование производится по значениям k от нуля до некоторого k _max.

При низких температурах можно пренебречь оптическими ветвями, поскольку они очень мало «заселены», а для акустических ветвей можно принять линейную зависимость 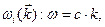поскольку заселены будут в основном их начальные линейные участки. Здесь с – некоторая «средняя скорость» звука, не учитывающая анизотропию упругих свойств кристаллов. Интеграл (15) можно брать по всему 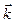- пространству, так как при низких температурах состояния с большими k почти не заселены. В результате получаем

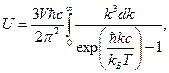(16)

или введя обозначение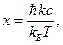

(17)

Интеграл является табличным и равен 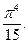Таким образом, при низких температурах получаем

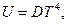(18)

где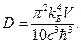

Тогда теплоемкость будет равна

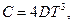(19)

что находится в согласии с экспериментом и не противоречит теореме Нернста, согласно которой теплоемкость тела должна стремиться к нулю при температуре, стремящейся к нулю.

Таким образом, теплоемкость кристаллической решетки вблизи 0К изменяется пропорционально третьей степени температуры. Это – закон кубов, теоретически установленный Дебаем. Закон кубов (19) относится только к теплоемкости кристаллической решетки. Для металлов к теплоемкости решетки надо добавить теплоемкость свободных электронов, которая меняется пропорционально первой степени температуры.

Оценим температуры, при которых справедливы выражения (8) и (19). Случай высоких температур имеет место, если 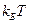>> ħ ω, где ω_max – максимальная частота звуковых колебаний в твердом теле, не превышает 10¹⁴ с^-1. Отсюда следует, что температура должна превышать ~100 К. Низкотемпературное приближение справедливо, если, во-первых, не будут заметно заселены оптические ветви и, во-вторых, закон дисперсии ω(k) можно считать линейным. Оба этих требования выполняются при 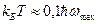, что дает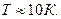

Теплоемкость при промежуточных температурах можно проанализировать, если для дисперсии фононов принять модельные законы. Такую удачную модельную закономерность предложил Дебай: линейный закон дисперсии 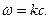Кроме того Дебай принял, что суммирование (или интегрирование) при расчете теплоемкости проводить не в пределах первой зоны Бриллюэна по всему 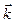- пространству, а по сфере радиуса k_D. Величина этого радиуса является подгоночным параметром, с помощью которого можно скомпенсировать отличие принятого закона дисперсии от реального для каждого твердого тела. Иными словами, зона Бриллюэна (иногда со сложной поверхностью) заменяется сферой в 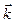- пространстве, имеющей одинаковый с ней объем.

С учетом указанных допущений формула (15) будет справедлива во всем диапазоне температур при условии, что волновое число изменяется в интервале от нуля до некоторого k_{D :}

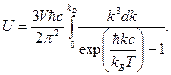(20)

Величину k_D можно определить из того, что общее число нормальных колебаний должно быть равно числу степеней свободы 3 N. Учитывая (14), имеем

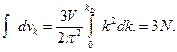(21)

Так как 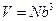(b – постоянная решетки), находим

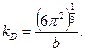(22)

Это значение можно выразить через волновое число, соответствующее границе первой зоны Бриллюэна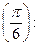

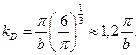(23)

Введем «характеристическую дебаевскую температуру», определяемую формулой

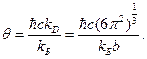(24)

Тогда формулу (20) для одного моля можно представить в виде

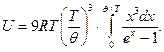(25)

Дифференцируя это соотношение по температуре, получаем интерполяционную формулу Дебая для молярной теплоемкости твердого тела

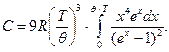(26)

При 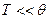верхний предел интеграла будет очень большим, сам интеграл уже не будет зависеть от температуры, и теплоемкость окажется пропорциональной кубу температуры (19). При 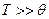теплоемкость будет 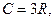что соответствует закону Дюлонга и Пти (8). Расчет по формуле (26) показывает, что при Т = θ теплоемкость составляет 95% от 3 R, т.е. характеристическая температура Дебая θ является верхней границей области температур, в которой при вычислении теплоемкости необходим квантовый подход.

Формула Дебая хорошо описывает зависимость теплоемкости от температуры лишь для тел с простыми кристаллическими решетками. К телам с более сложной структурой формула (26) неприменима. Связано это с тем, что у таких тел спектр колебаний оказывается очень сложным.

Итак, выше была рассмотрена так называемая решеточная теплоемкость, обусловленная тепловыми колебаниями кристаллической решетки. Рассмотрим теперь вклад в теплоемкость, обусловленной наличием свободных электронов.

Для его определения найдем среднюю энергию свободных электронов. Поведение электронов в металлах подчиняется распределению Ферми – Дирака, с учетом которого выражение для средней энергии можно представить в виде

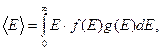(27)

где f (E) – функция распределения Ферми-Дирака

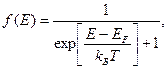(28)

где g (E) dE – число состояний электронов с энергией, заключенной в интервале от Е до dE. Для функции g (E) выполняется условие нормировки

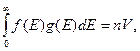(29)

где n – концентрация свободных электронов.

Отметим, что нагревание металла сопровождается переходом электронов с уровней вблизи уровня Ферми E_F (0) на уровни, расположенные выше E_F (0). Следовательно, в процессе нагревания металла будет воспринимать энергию только небольшая доля электронов, равная примерно 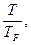где 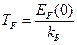- температура Ферми. Все другие электроны будут «заморожены» принципом запрета Паули. Таким образом, вклад электронов в значение теплоемкости составит величину

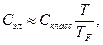(30)

где С_класс – классическая величина молярной теплоемкости электронного газа

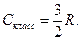(31)

Множитель 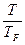существенно уменьшает классическое значение теплоемкости. Его величина при комнатных температурах в таком металле, как натрий, порядка 10^-2, т.е. электроны практически не вносят никакого вклада в теплоемкость металлов.

Дата добавления: 2014-01-11