Елементарні перетворення матриці

Метод елементарних перетворень для знаходження рангу матриці.

За допомогою елементарних перетворень, які не змінюють ранг матриці, зводимо матрицю до діагонального вигляду. Число відмінних від нуля елементів, розташованих на головній діагоналі, визначає ранг матриці.

.

1. Заміна рядків стовпцями, а стовпців відповідними рядками.

2. Переставлення двох будь-яких рядків (стовпців).

3. Викреслення рядка (стовпця), всі елементи якого дорівнюють нулю.

4. Множення всіх елементів будь–якого рядка (стовпця) на одне і те саме число відмінне від нуля.

5. Додавання до елементів одного рядка (стовпця), елементів іншого рядка (стовпця), помножених на довільне число.

Будь-яку матрицю шляхом елементарних перетворень можна привести до діагональної форми.

Означення. Дві матриці називаються еквівалентними, якщо від кожної з них можна перейти до другої за допомогою скінченого числа елементарних перетворень.

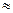Позначають еквівалентні матриці АВ.

Дата добавления: 2014-01-11