
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойство гидростатического давления. Основной закон гидростатики
|
|
|
|
В покоящейся жидкости выделим элементарный (очень малый) объем в виде тетраэдра, грани которого обозначим D Sx, D Sy, D Sz, D Sn. Нижний индекс указывает, какой оси координат перпендикулярна грань тетраэдра. Чтобы при выделении объема состояние жидкости в нем не изменилось, действие на него окружающей среды заменим соответствующими силами: поверхностными и массовыми. Поскольку жидкость покоится, на грани тетраэдра действуют со стороны окружающей среды только нормальные напряжения - давления (в соответствии с законом трения Ньютона в покоящейся жидкости касательные напряжения равны нулю), а на массу жидкости в объеме тетраэдра действует сила тяжести 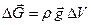 с напряжением
с напряжением 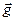 (рис.3.2).
(рис.3.2).
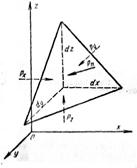 Рис. 3.2
Рис. 3.2
| Таким образом, на грани тетраэдра действуют давления px, py, pz, pn, создающие соответствующие нормальные силы:
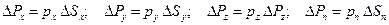 .
Условие равновесия тетраэдра – результирующая всех внешних сил, действующих на выделенный объем, равна .
Условие равновесия тетраэдра – результирующая всех внешних сил, действующих на выделенный объем, равна
|
нулю – в проекции на ось x принимает следующий вид:
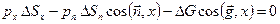 .
.
Поскольку
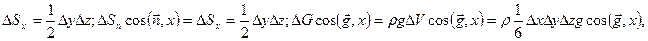
то уравнение равновесия принимает вид:
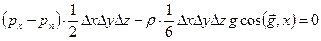 .
.
Сокращая на 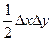 Dz и стягивая объем в точку (
Dz и стягивая объем в точку (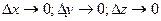 ), в пределе получим:
), в пределе получим: 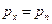 . Записывая условия равновесия в проекциях на оси y и z, получим, что и
. Записывая условия равновесия в проекциях на оси y и z, получим, что и 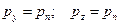 . Такое обстоятельство, что в любой точке покоящейся жидкости
. Такое обстоятельство, что в любой точке покоящейся жидкости 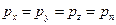 означает, что в этой точке давление не зависят от направления, от ориентации элементарной площадки. Этот закон изотропии давления в точках сплошной среды, находящейся в равновесии, был открыт в середине XVII в. Б. Паскалем.
означает, что в этой точке давление не зависят от направления, от ориентации элементарной площадки. Этот закон изотропии давления в точках сплошной среды, находящейся в равновесии, был открыт в середине XVII в. Б. Паскалем.
Выделим теперь в жидкости, покоящейся в поле силы тяжести элементарный объем в виде прямоугольного параллелепипеда с ребрами dx, dy, dz так, что ребро dz было бы параллельно ускорению свободного падения (рис.3.3).
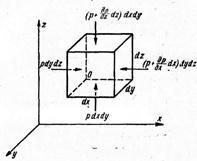 Рис. 3.3 Рис. 3.3
| Запишем уравнения равновесия этого объема в поле силы тяжести. На нижнюю грань выделенного объема вдоль оси z действует давление p с силой pdxdy. На верхнюю грань действует давление 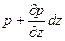 с силой с силой
|
(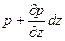 ) dxdy, направленной противоположно оси z. В этом же направлении действует и сила тяжести dG=rgdxdydz. В направлении осей x и y никаких сил, кроме сил давления не действует. Уравнения равновесия в проекциях на оси координат будут такими:
) dxdy, направленной противоположно оси z. В этом же направлении действует и сила тяжести dG=rgdxdydz. В направлении осей x и y никаких сил, кроме сил давления не действует. Уравнения равновесия в проекциях на оси координат будут такими:
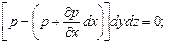
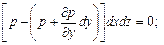
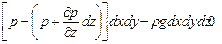 .
.
После сокращений получим:
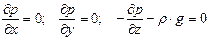 .
.
Из полученных уравнений видим, что давление p изменяется только под действием силы тяжести, действующей в нашем случае в направлении, противоположном оси z. Поэтому частную производную 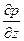 можно заменить полной и условие равновесия единицы объема жидкости в поле силы тяжести записать в виде основного уравнения гидростатики в дифференциальной форме:
можно заменить полной и условие равновесия единицы объема жидкости в поле силы тяжести записать в виде основного уравнения гидростатики в дифференциальной форме:
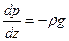 или
или 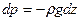 . (3.1)
. (3.1)
Из этих уравнений видно, что в поле силы тяжести с увеличением высоты (расстояния от поверхности Земли) давление в жидкости уменьшается. Проинтегрировать основное уравнение гидростатики можно, если известна зависимость плотности от давления. Если жидкость несжимаема (r=const.), то плотность не зависит от давления и давление будет равно после интегрирования:
p= - rgz+const.
Постоянную интегрирования нужно определять из граничных условий.
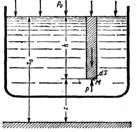
Пусть, например, жидкость находится в сосуде, и ее свободная поверхность располагается на высоте z о (рис.3.4). На свободную поверхность действует давление p 0. Необходимо определить давление на высоте z в точке М. Уравнение равновесия для единицы объема жидкости на свободной поверхности z=zо (Рис. 3.4): p 0 = - rgz 0 +const. (3.2)
 0 0
Рис.3.4
0 0
Рис.3.4
| Для единицы объема жидкости на высоте z основ-ное уравнение гидростатики: p= - rgz+ const (3.3).
или
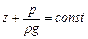 . (3.3а)
Из уравнения (3.2) находим const= p о+ rgz а и . (3.3а)
Из уравнения (3.2) находим const= p о+ rgz а и
|
подставляем ее в уравнение (3.3): p=p о+ rg (z о -z).
Если ввести переменную h=z - z0, которую назовем глубиной погружения, то основной закон гидростатики для несжимаемой жидкости будет выглядеть таким образом:
p= p 0+ rgh, (3.4)
которое можно прочитать так: давление в любой точке покоящейся жидкости складывается из давления на свободную поверхность жидкости p 0 и веса столба жидкости rgh, или избыточного давления. Когда давление на свободную поверхность в открытых сосудах равно атмосферному, то говорят, что абсолютное давление равно сумме барометрического и манометрического давлений (атмосферное давление измеряют барометром, а избыточное давление – манометром). Если абсолютное давление ниже атмосферного, то разность между ним и атмосферным называют вакуумметрическим давлением или вакуумом.
Таким образом, различают следующие виды давления: атмосферное (барометрическое), абсолютное (полное), манометрическое и вакуумметрическое. Барометрическое В (атмосферное pа) давление зависит от высоты места над уровнем Мирового океана и от погоды. За нормальное барометрическое давление принимают давление, равное 760 мм рт.ст., что соответствует pа= 101 325 н/м2. На уровне океана атмосферное давление наблюдалось в пределах от 90 000 н/м2 до 110 000 н/м2.
Давление, вычисляемое по формуле (3.4), называют абсолютным (полным). Когда давление на свободную поверхность равно атмосферному, т.е. p 0 =pa, то основное уравнение гидростатики перепишется так:
p = pa + ρgh ≡ pa+pм ≡ pa+∆p.
Таким образом, манометрическим давлением называют разность между абсолютным давлением p и атмосферным pa, если p>pa.
Когда в жидкости давление меньше атмосферного, то разность между атмосферным и абсолютным давлением называется вакуумметрическим давлением:
p вак= pa - p.
В этом случае абсолютное давление в жидкости вычисляется как:
p=pa - ρgh≡pa - p вак≡ pa - Δp.
Следствия:
1. с увеличением глубины погружения давление возрастает по линейному закону и тем быстрее, чем больше плотность жидкости;
2. на сколько изменилось давление на свободной поверхности, на столько оно изменится в любой точке жидкости.
Пример использования 2 следствия из основного уравнения гидростатики для несжимаемой жидкости. На рис.3.5 представлена схема гидравлической тормозной системы задних колес автомобиля.
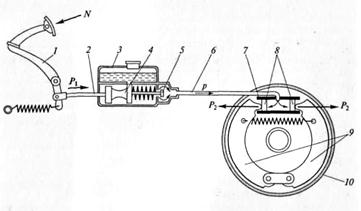
| Рис.3.5. N - ножная педаль; 2 — толкатель; 3 — главный тормозной цилиндр; 4 — поршень; 5 — клапан; 6 — трубопровод; 7 — колесный тормозной цилиндр; 8 — поршни; 9 — тормозные колодки; 10 — тормозной барабан; N — сила, приложенная к педали 1, р — давление в системе; Р1, — сила, действующая на поршень 4; Р2 — сила, создаваемая поршнями 8 |
Сила, приложенная к педали N, передается через толкатель 1 поршню 4 главного тормозного цилиндра 3, в котором создается давление
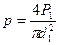 , где P1 — сила, действующая на поршень 4; d1 — диаметр поршня 4.
, где P1 — сила, действующая на поршень 4; d1 — диаметр поршня 4.
Вытесняемая жидкость поступает по трубопроводу 6 к колесному тормозному цилиндру 7 и действует на поршни 8, которые развивают силу P2=pπd22/4,
где р — давление, создаваемое в главном тормозном цилиндре; d2 — диаметр поршней 8.
Поршни 8, перемещаясь, прижимают колодки 9 к тормозному барабану 10, осуществляя торможение колеса.
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 913; Нарушение авторских прав?; Мы поможем в написании вашей работы!