Закон Архимеда

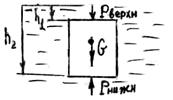Рис.3.6

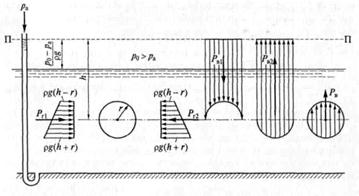Рис.3.7

К рис.3.7. r — радиус цилиндра; h — глубина погружения оси цилиндра; pg(h - r), pg(h + r) — давление на глубине h - r и h + r соответственно; Р_г1 и Р_г2 — горизонтальные составляющие силы давления на цилиндрическую поверхность; Р_в1 и Р_{в 2} — вертикальные составляющие силы давления на верхнюю и нижнюю части погруженного тела; Р_в — вертикальная составляющая силы давления на погруженное тело.

Рассмотрим твердое тело, погруженное в покоящуюся жидкость (рис.3.6, 3.7). Оно находится под действием двух сил, имеющих вертикальное направление: массовой силы G – веса тела, и поверхностной – результирующей силы давления жидкости P, окружающей тело. Результирующая сил давления в горизонтальном направлении равна нулю – силы давления, действующие на боковые поверхности справа и слева на тело, уравновешивают друг друга. Результирующую силу давления можно представить суммой двух составляющих P=P _верхн. +P _нижн..

Составляющая P _верхн действует сверху на тело в направлении силы тяжести, погружая тело. Составляющая P _нижн действует на нижнюю поверхность тела, выталкивая его на поверхность, поскольку давления во всех точках нижней поверхности в соответствии с основным законом гидростатики больше давлений в точках верхней поверхности. Разность этих сил: 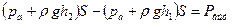выталкивает тело на поверхность, или 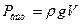, где V – объем тела, по-груженного в жидкость, а ρ gV – вес жидкости в объеме тела. Закон Архимеда теперь можно сформулировать так: погруженное в покоящуюся жидкость тело испытывает со стороны жидкости вертикальное подъемное усилие, равное весу жидкости в объеме погруженного тела. Точка приложения результирующей силы давления, выталкивающей тело, называется центром давления.

Пример 3.1. Определить глубину погружения железобетонного понтона, имеющего форму параллелепипеда высотой h= 1,8 м, шириной b= 2,5 м, длиной l= 6 м. Плотность бетона r _б=2500 кг/м³, толщина стенок понтона d =0,1 м.

Решение. Вес понтона равен

G=r _б gV==r _б g [2 lbd + 2 b (h- 2 d) d + 2(l- 2 d)(h- 2 d) d ]=139 кН.

Силу выталкивания (подъемную силу) определяем в соответствии с законом Архимеда, – она равна весу воды, вытесненной погруженной части тела, который, в свою очередь, при плавании понтона в воде, равен весу понтона:

P _выт= rgV _погр= rgblh ₁= G.

Откуда глубина погружения понтона h ₁ будет равна:

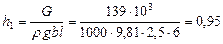м.

Пример. Изменение давления по высоте атмосферы

Используем дифференциальное уравнение основного закона гидростатики для сжимаемой жидкости - газа. Задача формулируется следующим образом: найти закон изменения давления по высоте нижнего слоя атмосферы Земли, толщиной 11 км - тропосферы. Известно, что по высоте тропосферы температура воздуха убывает по линейному закону: Т = Т₀ - β·Н.

Решение.

1. Для контрольного объема - атмосферы записываем уравнение основного закона гидростатики в дифференциальной форме

dp= - ρ·g·H.

2. Затем записываем уравнение, описывающее свойство газа - уравнение состояния

p = ρ·R·T.

3. Выражаем из уравнения (2) плотность, используя закон изменения температуры по высоте

.

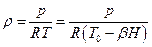4. Подставляем формулу для переменной по высоте тропосферы плотности в уравнение (1)

.

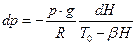5. Для проведения интегрирования разделяем переменные

.

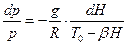6. Интегрируем в пределах: справа от Н = 0, до Н; слева - от р = р ₀ до р

.

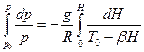7. После интегрирования и потенцирования получаем выражение

,

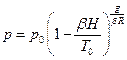по которому можно видеть, что давление с увеличением высоты убывает.

Контрольные вопросы

1. Какие напряжения вызывает сила, величина которой определяется по второму закону Ньютона? Зависят ли эти напряжения от направления?

2. Какие напряжения в жидкости вызывает давление, действующее на свободную поверхность? Как направлены эти напряжения?

3. На сколько изменится давление в любой точке покоящейся жидкости, если плотность ее увеличится в два раза? Изменится ли давление на свободной поверхности?

4. Скалярной, векторной или тензорной величиной являются массовые напряжения в любой точке жидкости?

5. Как направлены массовые напряжения, вызванные силой тяжести, в любой точке земной поверхности?

6. Какое тело будет более остойчивым (не опрокинется): у которого центр давления ниже центра тяжести или у которого центр давления выше центра тяжести?

7. Какими силами, поверхностными или массовыми, обусловлено плавание тела?

8. В каком виде находилась бы жидкость на Земле, если бы отсутствовала сила тяжести?

9. При каком условии получено уравнение свободной поверхности вращающейся жидкости?

10. Как математически показать, что жидкость ньютоновская?

11. Почему в соответствии с законом трения Ньютона в покоящейся жидкости касательные напряжения равны нулю?

12. Связаны ли поверхностные и массовые напряжения в жидкости между собой? Если связаны, то привести пример такой связи.

13. Какие напряжения вызывает сила, величина которой определяется по второму закону Ньютона? Зависят ли эти напряжения от направления?

14. Какие напряжения в жидкости вызывает давление, действующее на свободную поверхность? Как направлены эти напряжения?

15. На сколько изменится давление в любой точке покоящейся жидкости, если плотность ее увеличится в два раза? Изменится ли давление на свободной поверхности?

16. Скалярной, векторной или тензорной величиной являются массовые напряжения в любой точке жидкости?

17. Какое тело будет более остойчивым (не опрокинется): у которого центр давления ниже центра тяжести или у которого центр давления выше центра тяжести?

Дата добавления: 2014-01-11