Уравнение неразрывности. К классу одномерных течений можно отнести течение в элементарной струйке или в гипотетическом канале

ОДНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ

ЛЕКЦИЯ 9

К классу одномерных течений можно отнести течение в элементарной струйке или в гипотетическом канале, в которых параметры течения в каждом из поперечных сечений постоянны, т.е. p=p(x), T=(x) и т.д. Аналогичным образом и скорость u, направленная по нормали к сечению, должна быть постоянной в каждом из этих сечений: u=u(x). Если течение не является стационарным, то все эти величины также будут функциями времени t.

Обусловленные ограничения не так уже и велики, как это могло бы казаться. Зачастую их можно использовать для таких течений, где параметры не постоянны по сечению, предполагая при этом, что мы имеем дело с должным образом выбранными средними значениями.

В дальнейшем будем изучать установившееся течение жидкости.

Запишем уравнение неразрывности в интегральной форме для установившегося одномерного течения.

Граничные условия – боковые стенки контрольного объема непроницаемы.

Решение. Для выполнения условий задачи используем уравнение (4.6). Контрольную поверхность S представим суммой

S=S ₁+ S ₂+ S _б,

в которой S ₁ – поверхность, через которую жидкость втекает в контрольный объем; S ₂ – поверхность контрольного объема, через которую жидкость вытекает; S _б – боковая поверхность контрольного объема. Уравнение (4.6) в таком случае можно, поэтому представить также в виде суммы трех членов:

.

Поскольку по условию задачи течение одномерное, то параметры течения на входе и выходе контрольного объема по сечению не меняются; третье слагаемое из-за непроницаемости боковой поверхности равно нулю и уравнение неразрывности для канала с непроницаемой боковой поверхностью принимает такую форму:

или 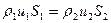, или ruS=const. (5.1)

Это уравнение говорит о том, что в канале с непроницаемыми боковыми стенками массовый расход G=ruS постоянен в любом поперечном сечении канала, не изменяется по длине канала. Уравнение (5.1) часто называют уравнением расхода.

1. Записать уравнение неразрывности в дифференциальной форме для одномерного установившегося течения в канале переменного сечения с непроницаемыми боковыми стенками.

Для решения этой задачи удобнее всего использовать уравнение расхода (5.1), его необходимо продифференцировать по координате:

.

Дата добавления: 2014-01-11