Уравнение движения. Интегральную форму уравнения движения для одномерного течения получим как частный случай пространственного течения

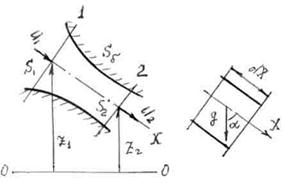
Интегральную форму уравнения движения для одномерного течения получим как частный случай пространственного течения. Рассматриваем одномерный поток в канале переменного сечения, ограниченный сечениями 1 и 2

а) б) Рис.5.1

(рис.5.1). Контрольная поверхность может быть представлена суммой трех поверхностей: S=S1+S2+S б. Уравнение движения (4.12) для рассматриваемых условий принимает вид: . Интеграл количества движения по площади

входа в объем S₁ равен:

.

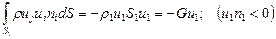Интеграл количества движения по площади выхода S₂ из объема равен:

.

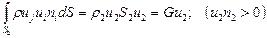Интеграл по боковой поверхности канала равен нулю в силу непроницаемости стенок.

Интегралы давлений по поверхностям S ₁ и S ₂ соответственно равны:

.

Вдоль боковой поверхности распределение давлений неизвестно, поэтому силу давления окружающей среды на боковую поверхность потока обозначим так:. Интеграл вязких напряжений равен:

.

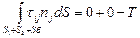Здесь T – сила трения, действующая со стороны окружающей среды на боковую поверхность потока; она направлена против движения и поэтому отрицательна. Интеграл вязких напряжений по поверхностям S ₁ и S ₂ равен нулю, т.к. вдоль этих поверхностей отсутствует градиент скорости. Сила тяжести, действующая на жидкость в контрольном объеме равна 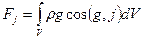. Теперь уравнение движения в проекции на какое-то направление j принимает такое выражение:

. (5.2)

Назовем 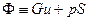полным потоком импульса, полным импульсом. Тогда для канала с прямолинейной осью, расположенной горизонтально, уравнение движения станет таким:

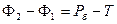. (5.3)

Это уравнение можно сформулировать так: изменение полного импульса жидкости в канале вызывается силовым действием на поток боковых стенок.

Дата добавления: 2014-01-11