Газодинамические функции расхода

Рассмотрим отношение плотности тока 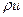к плотности тока в критическом сечении :

.

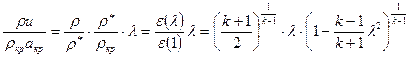Полученное отношение показывает, что оно зависит только от приведенной скорости. Поскольку плотность тока есть массовый расход, приходящийся на единицу площади, то отношение

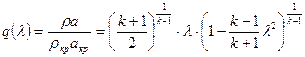(5.29)

называют газодинамической функцией расхода q(l). Чтобы построить ее график, вычислим значение функции в характерных точках:

l= 0; q (0)=0; l= 1; q (1)=1; l=l_m; q (l_m)=0.

Таким образом, на границах области изменения аргумента, функция q(l) имеет нулевые значения, а внутри интервала определения всюду положительна. Следовательно, имеется экстремум в виде максимума при l =1 (рис.5.3). Этот максимум разделяет газовый поток на две области: дозвуковую, где 0£l£1, и сверхзвуковую, в которой приведенная скорость изменяется в интервале 1£l£l _m.

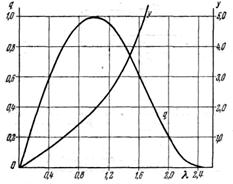Рис.5.3

В дозвуковой области течения с увеличением скорости течения (dl> 0) увеличиваются и значения газодинамической функции q(l) (dq(l)> 0), т.е. в дозвуковой области течения . В сверхзвуковом потоке производная . Покажем, как газодинамическая функ-

ция расхода q(l) применяется при вычислении массового расхода газа. Для этого запишем формулу для расхода и проделаем следующие действия:

.

Обозначим 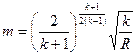. Эту величину назовем газодинамическим коэффициентом. Тогда формула для вычисления расхода в одномерном потоке идеального газа будет выглядеть следующим образом:

(5.30)

В критическом сечении S=S _кр, l= 1, q(l)= 1 и массовый расход равен:

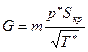. (5.31)

Если поделить формулу (5.30) на (5.31), то выявится геометрический смысл газодинамической функции расхода:

. (5.32)

В том случае, когда неудобно в расчетах или опытах пользоваться давлением заторможенного потока p^*, применяют другую газодинамическую функцию расхода. Она создается следующим способом:

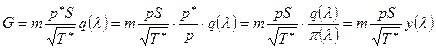. (5.33)

Газодинамическая функция расхода y (λ)

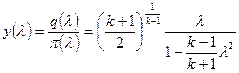(5.34)

изменяется без экстремума во всем диапазоне изменения приведенной скорости l (рис.5.3).

Контрольные вопросы

1. Как изменяется местная скорость звука с увеличением (уменьшением) местной скорости газа? Каковы предельные значения скорости звука в газовом потоке?

2. Вывести формулу для критической скорости.

3. Как изменяется внутренняя энергия при увеличении (уменьшении) скорости газа? Укажите предельные значения внутренней энергии.

4. Какие значения будут иметь температура и давление, когда скорость газа примет максимальное значение, минимальное значение?

5. Как изменяется значение критической скорости при увеличении статической температуры?

6. При ускорении газового потока как изменяются параметры состояния – давление, плотность и температура? Какой параметр состояния изменяется быстрее?

7. Какому закону сохранения соответствуют газодинамические функции параметров торможения?

8. Провести вывод газодинамических функций параметров торможения через число Маха.

9. Определить значения газодинамической функции расхода y(l) в харак-терных точках области определения приведенной скорости l. При определении численного значения положить значение k=1/4. Построить график y(l).

10. Какому закону сохранения соответствуют газодинамические функции расхода?

11. Как изменяется газодинамическая функция расхода q( λ) c увеличением приведенной скорости?

12. Как изменяется газодинамическая функция расхода q( λ) c увеличением приведенной скорости?

13. На основе какого уравнения определяется связь между безразмерными скоростями – числом Маха и приведенной скоростью?

14. При каких скоростях газового потока значения приведенной скорости и число Маха совпадают?

15. Выразить газодинамические функции расхода через число Маха.

Дата добавления: 2014-01-11