Ламинарное течение в круглых трубах

Примеры решения задач гидравлики

ЛЕКЦИЯ 14

В предыдущих разделах были рассмотрены основные физические характеристики движущейся жидкости, выведены уравнения законов сохранения, которым подчиняется движение жидкости, указана методика решения задач гидравлики. Проиллюстрируем эту методику на некоторых примерах.

Будем рассматривать равномерное движение несжимаемой ньютоновской жидкости в цилиндрической трубе. Целью изучения является нахождение закономерностей распределения скорости по поперечному сечению канала, распределения давления по длине трубы, определение расхода и других характеристик движения, которые необходимы для пользования уравнениями законов сохранения.

Сначала рассмотрим, при каких условиях можно получить равномерное движение жидкости. Предположим, что жидкость поступает в трубу с однородным профилем скорости. Под действием вязкости происходит перераспределение скорости по поперечному сечению вдоль трубы. Слои жидкости у стенки тормозятся, а центральная часть потока движется ускоренно. Толщина слоев приторможенной жидкости постепенно увеличивается, пока не станет равной радиусу трубы (рис.6.1).

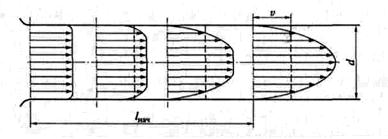Рис. 6.1 Схема течения на начальном участке и зависимости поправочного коэффициента к и коэффициента Кориолис а

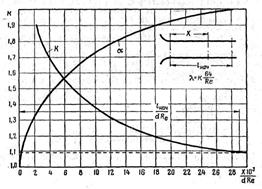
Участок трубы, на котором происходит нарастание слоев заторможенной жидкости, называется начальным участком течения. За пределами этого участка течение имеет постоянный профиль скорости. Длина начального участка для ламинарного течения, как уже упоминалось ранее, может быть определена по формуле Шиллера: l/d = 0,03 Re. Сопротивление начального участка трубы больше, чем на последующих участках стабилизированного течения, так как больше поперечные градиенты скорости du/dy. Потери давления на участке трубы, длина которого l < l _нач, необходимо определять с поправочным коэффи-циентом к, большим единицы, коэффициент Кориолиса же меньше, чем на участке стабилизированного течении (рис.6.2). Будем рассматривать ламинарное течение на основном участке трубы – после начального участка (рис. 6.2).

1 2

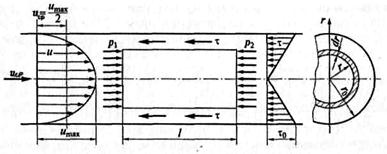
Рис.6.2 Расчетная схема

Выделяем контрольный объем длиной l и диаметром, равным диаметру трубы d. На рассматриваемом участке выделим цилиндрический объем радиуса r с основаниями в выбранных сечениях 1 – 2. Для выбранного участка запишем уравнение движения в полных импульсах (5.3):

.

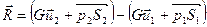На поверхности выделенного элементарного объема действуют нормальные и касательные напряжения: давление p и вязкие напряжения t. Сила давления, действующая на боковую поверхность в проекции на ось трубы равна нулю; параллельно оси, следовательно, действует только сила трения, направленная против потока и равная .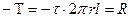

Граничные и начальные условия: так как канал цилиндрический и движение жидкости равномерное, то, в соответствии с уравнением неразрывности, u₂=u₁, S₂=S=pr². Подставляя эти условия и выражение для силы, действующей на боковую поверхность в уравнение движения, получаем:

.

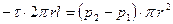Получившееся уравнение является условием равномерного движения: результирующая всех внешних сил, действующих на тело в направлении движения равна нулю (сила тяжести нормальна к направлению движения и поэтому не изменяет количество движения жидкости). Из этого уравнения находим выражение для касательных напряжений:

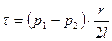, (6.1)

из которого видно, что вязкие напряжения распределены по сечению канала (по радиусу) линейно – максимальное значение вязкое напряжение имеет на стенке трубы (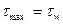). Для нахождения распределения скорости по сечению трубы необходимо привлечь к рассмотрению природу вязких напряжений, их связь с распределением скоростей. При изучении характеристик жидкости нами был рассмотрен закон трения Ньютона. В рассматриваемом случае он может быть записан в следующем виде:

.

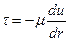Знак минус стоит потому, что радиус отсчитывается от оси, а не от стенки, на которой скорость жидкости равна нулю (в соответствии с гипотезой сплошности жидкости). Подставляем уравнение Ньютона в уравнение движения (6.1) и после разделения переменных имеем:

.

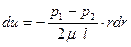Интегрирование позволяет получить выражение для скорости:

,

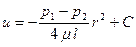в котором постоянную интегрирования C находим из граничных условий. На стенке трубы r=r₀; u= 0, откуда следует, что . После подстановки выражения для постоянной интегрирования будем иметь параболическое распределение скорости по радиусу трубы, определяемые законом распределения вязких напряжений:

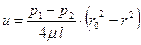. (6.2)

Из формулы (6.2) можно узнать, что максимальное значение скорости жидкость имеет на оси трубы:

.

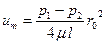С использованием выражения для максимальной скорости формула (5.2) принимает такой вид:

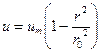. (6.2а)

С прикладной точки зрения распределение скорости необходимо для, определения объемного расхода. С этой целью все поперечное сечение трубы разобьем на множество элементарных площадок dS в пределах каждой из них скорость жидкости можно полагать постоянной, Тогда элементарный объемный расход dQ через площадку dS будет равен dQ=udS, а полный расход будет равен сумме элементарных расходов, которую можно записать в виде интеграла по площади:

.

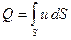Вычислить этот интеграл можно, используя формулу (5.2а) и выражение для элементарной площадки dS. Для последнего воспользуемся следующим соображением: элементарная площадка должна вычисляться на любом текущем значении радиуса r, поэтому эта площадка должна представлять элементарное кольцо (рис.5.2) площадью dS=2p rdr.

Тогда расход в любом сечении основного участка трубы может быть вычислен так:

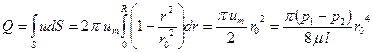. (6.3)

Формула (6.3) примечательна тем, что показывает очень сильную зависимость расхода от радиуса трубы - в четвертой степени. С точки зрения практики, небольшие отложения на стенках трубы приводят к значительному уменьшению расхода при одном и том же перепаде давления на трубе (разнице давления p ₁ -p ₂).

Среднерасходная или средняя скорость определяется как отношение расхода к площади поперечного сечения трубы:

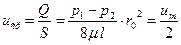. (6.4)

Для вычисления гидравлических потерь по длине трубы (путевых потерь) запишем уравнение Бернулли (4.4) для расчетного участка:

.

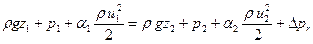Граничное условия z₁ = z ₂; равенство среднерасходных скоростей в граничных сечениях преобразовывают это уравнение к искомой формуле для путевых потерь давления:

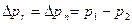. (6.5)

Формула (6.5) говорит, что из-за гидравлических (в данном случае путевых) потерь давление вдоль трубы уменьшается. Для заданной средней скорости, вязкости, геометрии трубы (l, r₀) путевые потери как вычисляются так:

.

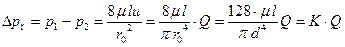Видно, что в ламинарном потоке потери давления пропорциональны расходу в первой степени. Коэффициент K называют сопротивлением трубопровода.

С другой стороны, в практике принято вычислять путевые потери по формуле Дарси:

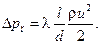
Здесь λ – коэффициент путевых потерь, зависящий, в общем случае, от числа Рейнольдса и шероховатости трубопровода. Число Рейнольдса Re вычисляется по формуле:

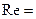
ud ρ/μ.

Приравнивая два выражения для путевых потерь и разрешая получившееся уравнение относительно коэффициента путевых потерь, получим:

.

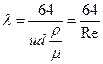Таким образом, при ламинарном течении коэффициент путевых потерь обратно пропорционален числу Рейнольдса и не зависит от шероховатости омываемой поверхности.

Можно вычислить и коэффициент Кориолиса, учитывающий неравномер-ность распределения кинетической энергии по сечению трубы:

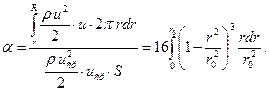
Произведем замену переменной:

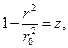
и тогда получим

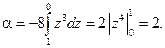
Итак, кинетическая энергия ламинарного потока в сечении круглой трубы (параболическим распределением скоростей) в два раза превосходит кинетичес-кую энергию того же потока, но при однородном распределении скорости

Контрольные вопросы.

1. Почему касательные напряжения максимальны на стенке трубы. Написать формулу для t_w.

2. Откуда видно, что скорость максимальна на оси трубы?

3. Как изменится величина путевых потерь давления при увеличении числа Re?

4. Какую форму должна иметь элементарная площадка dS при вычислении объемного расхода? Записать формулу для dS.

5. Как соотносятся между собой среднерасходная скорость и максимальная?

6. Как зависит потеря давления от расхода при ламинарном течении?

Дата добавления: 2014-01-11